

八年级数学秘籍——探索“手拉手”模型(解析版)学案
展开探索“手拉手”模型
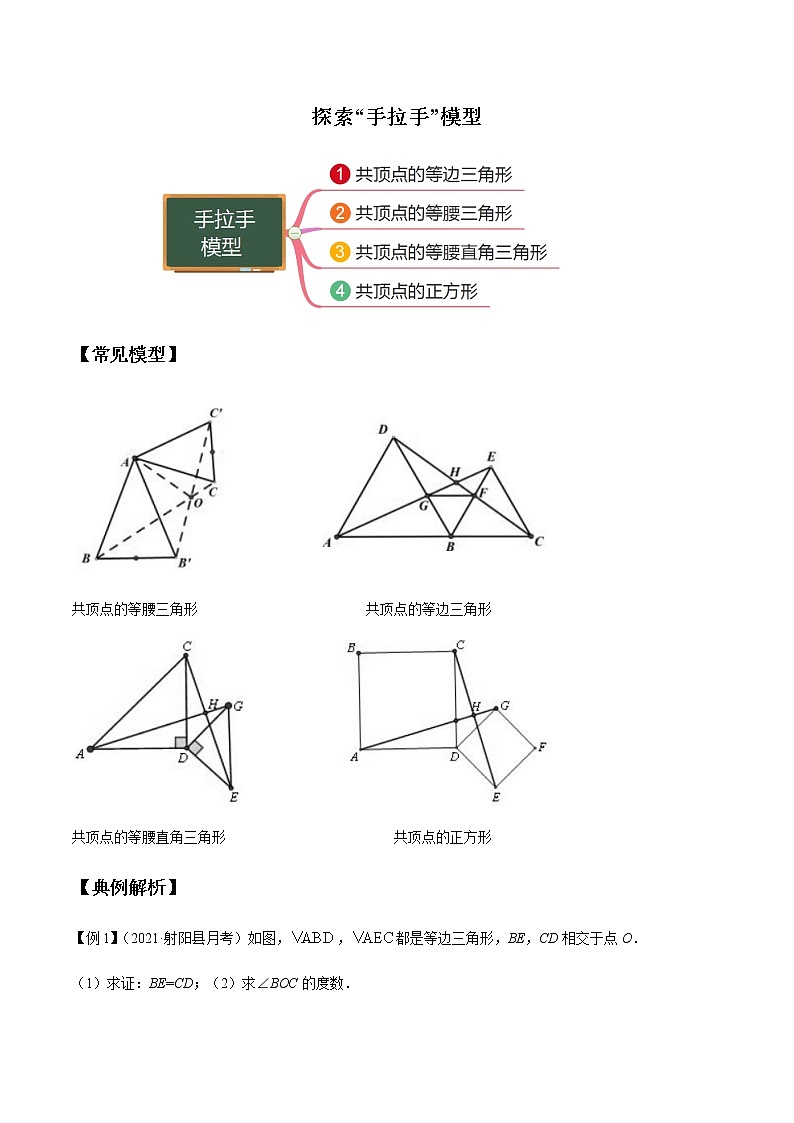
【常见模型】
共顶点的等腰三角形 共顶点的等边三角形
共顶点的等腰直角三角形 共顶点的正方形
【典例解析】
【例1】(2021·射阳县月考)如图,,都是等边三角形,BE,CD相交于点O.
(1)求证:BE=CD;(2)求∠BOC的度数.
【答案】见解析.
【解析】(1)证明:∵△ABD与△AEC都是等边三角形,
∴AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,,
∴△DAC≌△BAE(SAS),
∴BE=DC;
(2)由(1)可得出∠ADC=∠ABE,
∵∠BOD=180°-∠ODB-∠DBA-∠ABE
=180°-∠ODB-60°-∠ADC
=120°-(∠ODB+∠ADC)
=60°,
∴∠BOC=180°-∠BOD=180°-60°=120°.
【例2】(2020·常州市武进区月考)如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面的结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】D.
【解析】∵△ABD、△BCE为等边三角形,
∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠PBQ=60°,
∴△ABE≌△DBC,①正确;
∵△ABE≌△DBC,
∴∠BAE=∠BDC,
∵∠BDC+∠BCD=180°﹣60°﹣60°=60°,
∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,
∴②正确;
由△ABP≌△DBQ,
∴BP=BQ,
∴△BPQ为等边三角形,
∴③正确;
由全等三角形对应边上的高相等,知B到CD、AE的距离相等,
故BM平分∠AMC,
∴④正确;
综上所述:正确的结论有4个.
【例3】(2020·沙坪坝月考)已知:在中,,以为顶点作,连接.
(1)如图,若,求的面积:
(2)如图,若为的中点,连接并延长交于,求证:
(3)如图,为上一点,,连接为上一点,,连接,过作于,若,请直接写出的长.
【答案】见解析.
【解析】(1)解:∵BE=2.5
∴BD=BE=2.5
∵∠CBE=120°
∴∠ABD=60°
∵AD⊥BD
∴AB=2BD=5,
∴△ABC面积为:12.5.
(2)证明:过A作AM∥BD交BF延长线于M
∴∠M=∠FBD,∠MAB+∠ABD=180°
∵F为AD的中点
∴AF=DF
又∠1=∠2,
∴△AMF≌△DBF
∴AM=BD,
∴AM=BE,
∵∠CBE+∠ABD=180°,∠ABD+∠BAM=180°
∴∠CBE=∠BAM
∴△ABM≌△BCE
∴∠BEC=∠M=∠FBD
∵∠FBD+∠HBE=90°
∴∠BEC+∠HBE=90°
∴∠BHE=90°,即FH⊥CE.
(3)
在BF上取一点M,使得BM=DF,连接GM,过A作AN⊥BF于N,
可得:△GMB≌△GFD,得等边△GMF
故BF=FG+DF=9
由角平分线得:AH=AN,而S△ABF=10,故AH=.
【例4】(2020·湖南双清期末)以点为顶点作等腰,等腰,其中,如图1所示放置,使得一直角边重合,连接、.
(1)试判断、的数量关系,并说明理由;
(2)延长交于点试求的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
【答案】见解析.
【解析】解:
(1)∵△ABC、△ADE是等腰直角三角形,
∴AB=AC,∠BAD=∠EAC=90°,AD=AE,
在△ADB和△AEC中,
∴△ADB≌△AEC(SAS),
∴BD=CE.
(2)∵△ADB≌△AEC,
∴∠ACE=∠ABD,
在△CDF中,∠BFC=180°-∠ACE-∠CDF,
∵∠CDF=∠BDA,
∴∠BFC=180°-∠DBA-∠BDA=∠DAB=90°;
(3)BD=CE成立,∠BFC=90°.
理由如下:
∵△ABC、△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠EAD=90°,
∵∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△ADB和△AEC中,,
∴△ADB≌△AEC(SAS),
∴BD=CE,∠ACE=∠DBA,
∴∠BFC=∠DAB=90°.
【例5】(2019·河北安平期末)如图,和都是等腰直角三角形,,,则___________度.
【答案】132.
【解析】解:∵∠ACB=∠ECD=90°,
∴∠BCD=∠ACE
又AC=BC,CD=CE
∴△BDC≌△AEC
∴∠DBC=∠EAC
∵∠EBD=∠DBC+∠EBC=42°
∴∠EAC+∠EBC=42°,
∴∠ABE+∠EAB=48°
∴∠AEB=132°
故答案为:132.
【习题专练】
1.(2020·沈阳兴华月考)(1)问题发现与探究:
如图,都是等腰直角三角形,,点A,D,E在同一直线上,于点M,连接BD,则:
(1)线段AE,BD之间的大小关系是___________; ;
(2)求证:AD=2CM+BD;
【答案】(1)AE=BD,90°;(2)见解析.
【解析】(1)解:∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∵∠ACB=∠DCE=90°,
∴∠ACE=∠BCD,
在△ACE与△BCD中,
AC=BC,∠ACE=∠BCD,CE=CD,
∴△ACD≌△BCE,
∴AE=BD,∠AEC=∠BDC,
∵∠CED=∠CDE=45°,
∴∠AEC=135°,∴∠BDC=135°,∴∠ADB=90°;
故答案为:AE=BD,90°;
(2)证明:在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM=DM=ME,
∴DE=2CM,
∴AD=DE+AE=2CM+BD.
2.(2020·江阴市月考)如图,在和中,,连接交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为( ).
A.4 B.3 C.2 D.1
【答案】B
【解析】解:∵∠AOB=∠COD=40°
∴∠AOC=∠BOD
又OA=OB,OC=OD
∴△AOC≌△BOD
∴∠OCA=∠ODB,AC=BD,①正确;
∴∠OAC=∠OBD,
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40°,②正确;
过O作OG⊥CM于G,OH⊥BM于H,
可得:OG=OH,
∴OM平分∠BMC,④正确;
正确的个数有3个;
故答案为:B.
3.(2020·山东济阳期末)如图,与都是等边三角形,,下列结论中,正确的个数是( )①;②;③;④若,且,则.
A.1 B.2 C.3 D.4
【答案】C.
【解析】解:∵△ABD与△AEC是等边三角形
∴AD=AB,AC=AE,∠DAB=∠EAC=60°
∴∠DAB+∠BAC=∠EAC +∠BAC
即∠DAC=∠EAB
∴△DAC≌△BAE
∴BE=CD,①正确;
∵△DAC≌△BAE
∴∠ADO=∠ABO
∴∠BOD=∠DAB=60°,②正确
∵∠BDA=∠CEA=60°,∠ADC≠∠AEB
∴∠BDA-∠ADC≠∠CEA-∠AEB
∴∠BDO≠∠CEO,③错误
∵AD∥BC
∴∠DAC+∠BCA=180°
∵∠DAB=60°,∠BAC=90°
∴∠BCA=180°-∠DAB-∠BAC=30°
∵∠ACE=60°
∴∠BCE=∠ACE+∠BCA=60°+30°=90°
∴BC⊥CE,④正确
故由①②④三个正确,
故答案为:C.
4.(2020·重庆巴南月考)如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
【答案】见解析.
【解析】(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS);
(2)解:∵△ABD≌△ACE,
∴∠ABD=∠2=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
5.(2019·东北师大附中期末)已知和都是等腰三角形,,,.
(初步感知)(1)特殊情形:如图①,若点,分别在边,上,则__________.(填>、<或=)
(2)发现证明:如图②,将图①中的绕点旋转,当点在外部,点在内部时,求证:.
(深入研究)(3)如图③,和都是等边三角形,点,,在同一条直线上,则的度数为__________;线段,之间的数量关系为__________.
(4)如图④,和都是等腰直角三角形,,点、、在同一直线上,为中边上的高,则的度数为__________;线段,,之间的数量关系为__________.
(拓展提升)(5)如图⑤,和都是等腰直角三角形,,将绕点逆时针旋转,连结、.当,时,在旋转过程中,与的面积和的最大值为__________.
【答案】见解析.
【解析】[初步感知] =.
(2)成立.
理由:由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,,
∴△DAB≌△EAC(SAS),
∴DB=CE;
[深入探究](3)设AB,CD交于O,
∵△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAB=∠EAC,
在△DAB和△EAC中,,
∴△DAB≌△EAC(SAS),
∴DB=CE,∠ABD=∠ACE,
∵∠BOD=∠AOC,
∴∠BDC=∠BAC=60°;
(4)∵△DAE是等腰直角三角形,
∴∠AED=45°,
∴∠AEC=135°,
在△DAB和△EAC中,,
∴△DAB≌△EAC(SAS),
∴∠ADB=∠AEC=135°,BD=CE,
∵∠ADE=45°,
∴∠BDC=∠ADB-∠ADE=90°,
∵△ADE都是等腰直角三角形,AM为△ADE中DE边上的高,
∴AM=EM=MD,
∴AM+BD=CM;
故答案为:90°,AM+BD=CM;
【拓展提升】
(5)如图,
由旋转可知,在旋转的过程中△ADE的面积始终保持不变,
△ADE与△ADC面积的和达到最大,
∴△ADC面积最大,
∵在旋转的过程中,AC始终保持不变,
∴要△ADC面积最大,
∴点D到AC的距离最大,
∴DA⊥AC,
∴△ADE与△ADC面积的和达到的最大为2+×AC×AD=5+2=7,
故答案为7.
6. (2019·福建龙岩期末)已知点P是线段MN上一动点,分别以PM,PN为一边,在MN的同侧作△APM,△BPN,并连接BM,AN.
(Ⅰ)如图1,当PM=AP,PN=BP且∠APM=∠BPN=90°时,试猜想BM,AN之间的数量关系与位置关系,并证明你的猜想;
(Ⅱ)如图2,当△APM,△BPN都是等边三角形时,(Ⅰ)中BM,AN之间的数量关系是否仍然成立?若成立,请证明你的结论;若不成立,试说明理由.
(Ⅲ)在(Ⅱ)的条件下,连接AB得到图3,当PN=2PM时,求∠PAB度数.
【答案】(1)BM=AN,BM⊥AN.(2)结论成立.(3)90°.
【解析】解:(Ⅰ)结论:BM=AN,BM⊥AN.
理由:
∵MP=AP,∠APM=∠BPN=90°,PB=PN,
∴△MBP≌△ANP(SAS),
∴MB=AN.
延长MB交AN于点C.
∵△MBP≌△ANP,
∴∠PAN=∠PMB,
∵∠PAN+∠PNA=90°,
∴∠PMB+∠PNA=90°,
∴∠MCN=180°﹣∠PMB﹣∠PNA=90°,
∴BM⊥AN.
(Ⅱ)结论成立
理由:
∵△APM,△BPN,都是等边三角形
∴∠APM=∠BPN=60°
∴∠MPB=∠APN=120°,
又∵PM=PA,PB=PN,
∴△MPB≌△APN(SAS)
∴MB=AN.
(Ⅲ)取PB的中点C,连接AC,AB.
∵△APM,△PBN都是等边三角形
∴∠APM=∠BPN=60°,PB=PN
∵点C是PB的中点,且PN=2PM,
∴2PC=2PA=2PM=PB=PN,
∵∠APC=60°,
∴△APC为等边三角形,
∴∠PAC=∠PCA=60°,
又∵CA=CB,
∴∠CAB=∠ABC=30°,
∴∠PAB=∠PAC+∠CAB=90°.
7.(2019·江苏盐城期中)(1)(观察发现)如图 1,△ABC 和△CDE 都是等边三角形,且点 B、C、E 在一条直线上,连接 BD 和AE,BD、AE 相交于点 P,则线段 BD 与 AE 的数量关系是 ,BD 与 AE 相交构成的锐角的度数是 .(只要求写出结论,不必说明理由)
(2)(深入探究)如图 2,△ABC 和△CDE 都是等边三角形,连接 BD 和 AE,BD、AE 相交于点 P,猜想线段 BD 与 AE 的数量关系,以及 BD 与 AE 相交构成的锐角的度数. 请说明理由 结论:
理由:_______________________
【答案】(1)BD=AE,60°;(2)BD=AE,60°;(3)见详解.
【解析】解:(1)∵△ABC和△CDE都是等边三角形,
∴AB=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,,
∴△ACE≌△BCD(SAS),
∴BD=AE,∠AEC=∠BDC,
由三角形的外角性质,∠DPE=∠AEC+∠DBC,
∠DCE=∠BDC+∠DBC,
∴∠DPE=∠DCE=60°;
(2)结论BD=AE,∠DPE=60°还成立.
∵△ABC和△CDE是等边三角形,
∴AB=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,,
∴△ACE≌△BCD(SAS),
∴BD=AE,∠AEC=∠BDC,
∵∠BDC+∠CDE+∠AED
=∠AEC+∠CDE+∠AED
=∠CDE+∠CED
=180°-∠DCE
=180°-60°=120°,
∴∠DPE=180°-(∠BDC+∠CDE+∠AED)=180°-120°=60°;
8.(2019·内蒙古赛罕期中)如图,,均为等边三角形,点,,在同一条直线上,连接,,与相交于点,与相交于点,连接,下列结论正确的有_________.
①;②;③;④;⑤平分
【答案】①②③⑤.
【解析】解:∵△ABE,△BCD均为等边三角形,
∴AB=BE,BC=BD,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中,
∴△ABD≌△EBC(SAS),
∴AD=EC,故①正确;
∴∠DAB=∠BEC,
又由上可知∠ABE=∠CBD=60°,
∴∠EBD=60°,
在△ABM和△EBN中,
∴△ABM≌△EBN(ASA),
∴BM=BN,故②正确;
∴△BMN为等边三角形,
∴∠NMB=∠ABM=60°,
∴MN∥AC,故③正确;
若EM=MB,则AM平分∠EAB,
则∠DAB=30°,而由条件无法得出这一条件,
故④不正确;
作BG⊥AD,BH⊥CE,
可知△ABD≌△EBC,
∴两个三角形对应边的高相等,即BG=BH,
∴OB是∠AOC的角平分线,故⑤正确.
故答案为:①②③⑤.
9.(2020·安徽淮南月考)(提出问题)
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,连结CN.求证:CN∥AB.
图1
(类比探究)
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论CN∥AB还成立吗?请说明理由.
图2
【答案】见解析.
【解析】解:(1)∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠ABM=∠BAC=∠ACB=∠MAN=60º,
∴∠BAM+∠MAC=∠MAC+∠CAN,
∴∠BAM=∠CAN,又AB=AC,AM=AN,
∴△BAM≌△CAN(SAS),
∴∠ACN=∠ABM=60º,又∠ACB=60º,
∴∠ABM+∠BCN=180º,
∴CN∥AB;
(2)CN∥AB成立,理由如下:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠ABM=∠BAC=∠ACB=∠MAN=60º,
∴∠BAC+∠MAC=∠MAC+∠MAN,
∴∠BAM=∠CAN,AB=AC,AM=AN,
∴△BAM≌△CAN(SAS),
∴∠ACN=∠ABM=60º,又∠ACB=60º,
∴∠ABM+∠BCN=180º,
∴CN∥AB.
10.(2020·四川彭州期末)(1)如图1,和都是等边三角形,且,,三点在一条直线上,连接,相交于点,求证:.
(2)如图2,在中,若,分别以,和为边在外部作等边,等边,等边,连接、、恰交于点.
①求证:;
②如图2,在(2)的条件下,试猜想,,与存在怎样的数量关系,并说明理由.
【答案】见解析.
【解析】解:(1)证明:∵△BCD和△DCE都是等边三角形,
∴BC=AC,CE=CD,∠ACB=∠DCE=60°,
∴∠ABC+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)①证明:∵△ABC和△DCE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,
同理:△ABD≌△CBF(SAS),
∴AD=CF,
即AD=BE=CF;
②解:结论:PB+PC+PD=BE,
理由:
`
AD与BC的交点记作点Q,则∠AQC=∠BQP,
由①知,△ACD≌△BCE,
∴∠CAD=∠CBE,
在△ACQ中,∠CAD+∠AQC=180°-∠ACB=120°,
∴∠CBE+∠BQP=120°,
在△BPQ中,∠APB=180°-(∠CBE+∠BQP)=60°,
∴∠DPE=60°,
同理:∠APC=60°,
∴∠CPE=60°,∠CPD=120°,
在PE上取一点M,使PM=PC,
∴△CPM是等边三角形,
∴CP=CM=PM,∠PCM=∠CMP=60°,
∴∠CME=120°=∠CPD,
∵△CDE是等边三角形,
∴CD=CE,∠DCE=60°=∠PCM,
∴∠PCD=∠MCE,
∴△PCD≌△MCE(SAS),
∴PD=ME,
∴BE=PB+PM+ME=PB+PC+PD.
八年级数学秘籍——探索“一线三等角”模型(原卷版)学案: 这是一份八年级数学秘籍——探索“一线三等角”模型(原卷版)学案,共9页。学案主要包含了常见图形,典例解析,习题专练等内容,欢迎下载使用。
八年级数学秘籍——与角度、面积等相关的动态问题(解析版)学案: 这是一份八年级数学秘籍——与角度、面积等相关的动态问题(解析版)学案,共25页。学案主要包含了典例解析,变式1-1,变式1-2,变式2-1,习题专练等内容,欢迎下载使用。
八年级数学秘籍——尺规作图与最短路径(解析版)学案: 这是一份八年级数学秘籍——尺规作图与最短路径(解析版)学案,共38页。学案主要包含了典例解析,例1-1,例1-2,变式1-1,变式1-2,变式1-3,变式1-4,例2-1等内容,欢迎下载使用。












