【历年真题】2022年四川省渠县中考数学模拟测评 卷（Ⅰ）（含答案解析）

这是一份【历年真题】2022年四川省渠县中考数学模拟测评 卷（Ⅰ）（含答案解析），共22页。试卷主要包含了的值．等内容，欢迎下载使用。
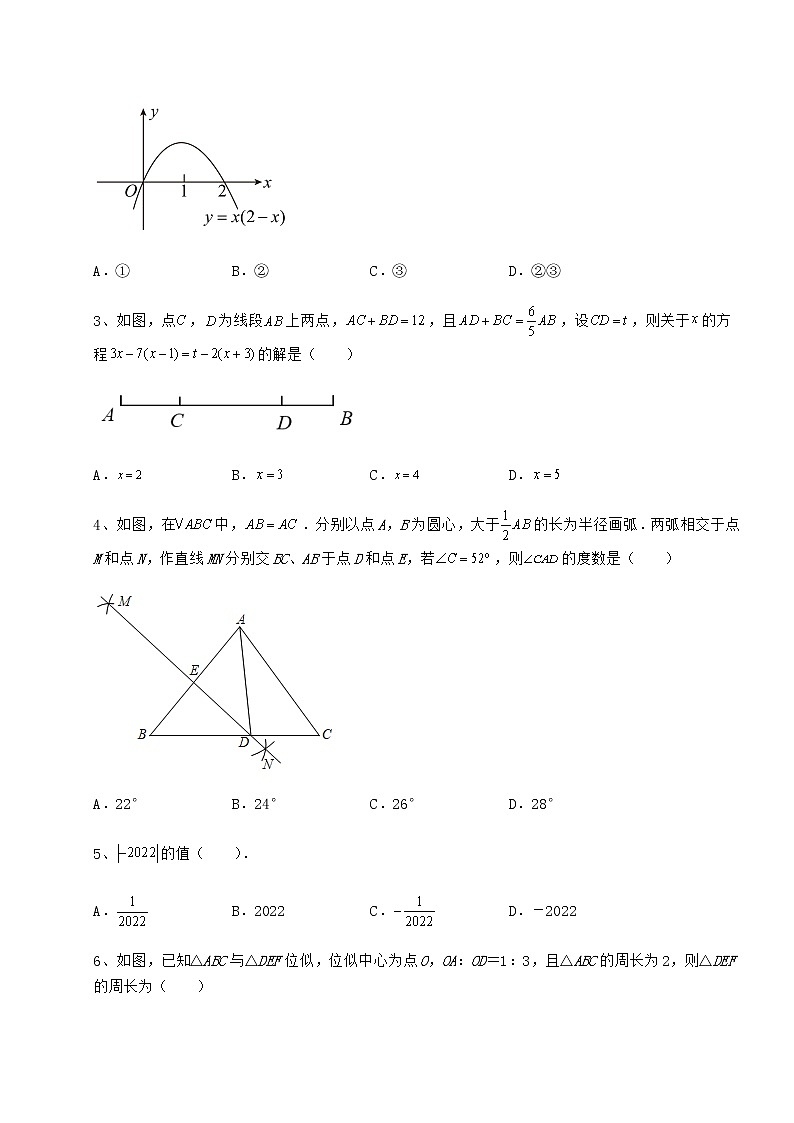
2022年四川省渠县中考数学模拟测评 卷（Ⅰ） 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，小玲将一个正方形纸片剪去一个宽为的长条后，再从剩下的长方形纸片上剪去一个宽为的长条，如果两次剪下的长条面积正好相等，那么原正方形的边长为（   ）cm．A． B． C． D．2、如图，要在二次函数的图象上找一点，针对b的不同取值，所找点M的个数，有下列三种说法：①如果，那么点M的个数为0；②如果．那么点M的个数为1；③如果，那么点M的个数为2．上述说法中正确的序号是（    ）A．① B．② C．③ D．②③3、如图，点，为线段上两点，，且，设，则关于的方程的解是（    ）A． B． C． D．4、如图，在中，．分别以点A，B为圆心，大于的长为半径画弧．两弧相交于点M和点N，作直线MN分别交BC、AB于点D和点E，若，则的度数是（    ）A．22° B．24° C．26° D．28°5、的值（    ）．A． B．2022 C． D．－20226、如图，已知△ABC与△DEF位似，位似中心为点O，OA：OD＝1：3，且△ABC的周长为2，则△DEF的周长为（　　）A．4 B．6 C．8 D．187、若方程有实数根，则实数a的取值范围是（    ）A． B．C．且 D．且8、如图，任意四边形ABCD中，E，F，G，H分别是各边上的点，对于四边形E，F，G，H的形状，小聪进行了探索，下列结论错误的是（　　　）A．E，F，G，H是各边中点．且AC=BD时，四边形EFGH是菱形B．E，F，G，H是各边中点．且AC⊥BD时，四边形EFGH是矩形C．E，F，G，H不是各边中点．四边形EFGH可以是平行四边形D．E，F，G，H不是各边中点．四边形EFGH不可能是菱形9、将抛物线y＝x2先向右平移3个单位长度，再向上平移5个单位长度，所得抛物线的解析式为（　　）A．y＝（x+3）2+5 B．y＝（x﹣3）2+5 C．y＝（x+5）2+3 D．y＝（x﹣5）2+310、有理数、、、在数轴上对应的点的位置如图所示，则下列结论错误的是（    ）A． B． C． D．第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图是两个全等的三角形，图中字母表示三角形的边长，则∠的度数为________º. 2、若a、b为实数，且，则的值是____．3、直接写出计算结果：（1）=____；（2）____；（3）=____；（4）102×98=____．4、如图，已知的三个角，，，，将绕点顺时针旋转得到，如果，那么_______．5、如图，在中，AB的垂直平分线交BC于D，AC的中垂线交BC于E，，则的度数为________．三、解答题（5小题，每小题10分，共计50分）1、如图，已知△ABC．（1）请用尺规在图中补充完整以下作图，保留作图痕迹：作∠ACB的角平分线，交AB于点D；作线段CD的垂直平分线，分别交AC于点E，交BC于点F；连接DE，DF；（2）求证：四边形CEDF是菱形．2、计算：．3、（数学阅读）图1是由若干个小圆圈推成的一个形如等边三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共推了n层．将图1倒置后与原图1排成图2的形状，这样图2中每一行的圆圈数都是．我们可以利用“倒序相加法”算出图1中所有圆圈的个数为：．（问题解决）（1）按照图1的规则摆放到第12层时，求共用了多少个圆圈；（2）按照图1的规则摆放到第19层，每个圆圈都按图3的方式填上一串连续的正整数：1，2，3，4，……，则第19层从左边数第二个圆圈中的数字是______．4、（1）．（2）．5、阅读材料：两点间的距离公式：如果直角坐标系内有两点A（x1，y1）、B（x2，y2），那么A、B两点的距离AB＝．则AB2＝（x1﹣x2）2+（y1﹣y2）2．例如：若点A（4，1），B（2，3），则AB＝根据上面材料完成下列各题：（1）若点A（﹣2，3），B（1，﹣3），则A、B两点间的距离是 　 　．（2）若点A（﹣2，3），点B在坐标轴上，且A、B两点间的距离是5，求B点坐标．（3）若点A（x，3），B（3，x+1），且A、B两点间的距离是5，求x的值． -参考答案-一、单选题1、B【分析】设正方形的边长为x cm，则第一个长条的长为x cm，宽为2cm，第二个长条的长为(x-2)cm，宽为3cm，根据两次剪下的长条面积正好相等列方程求解．【详解】解：设正方形的边长为x cm，则第一个长条的长为x cm，宽为2cm，第二个长条的长为(x-2)cm，宽为3cm，依题意得：2x=3(x-2)，解得x=6故选：B．【点睛】本题考查了由实际问题抽象出一元一次方程，找准等量关系，正值列出一元一次方程是解题的关键．2、B【分析】把点M的坐标代入抛物线解析式，即可得到关于a的一元二次方程，根据根的判别式即可判断．【详解】解：∵点M（a，b）在抛物线y=x（2-x）上， 当b=-3时，-3=a（2-a），整理得a2-2a-3=0，∵△=4-4×（-3）＞0，∴有两个不相等的值，∴点M的个数为2，故①错误；当b=1时，1=a（2-a），整理得a2-2a+1=0，∵△=4-4×1=0，∴a有两个相同的值，∴点M的个数为1，故②正确；当b=3时，3=a（2-a），整理得a2-2a+3=0，∵△=4-4×3＜0，∴点M的个数为0，故③错误；故选：B．【点睛】本题考查了二次函数图象上点的坐标特征，一元二次方程根的判别式，熟练掌握二次函数与一元二次方程的关系是解题的关键．3、D【分析】先根据线段的和差运算求出的值，再代入，解一元一次方程即可得．【详解】解：，，，，解得，则关于的方程为，解得，故选：D．【点睛】本题考查了线段的和差、一元一次方程的应用，熟练掌握方程的解法是解题关键．4、B【分析】由尺规作图痕迹可知MN垂直平分AB，得到DA=DB，进而得到∠DAB=∠B=50°，再利用等腰三角形的性质和三角形内角和计算出∠BAC，然后计算∠BAC-∠DAB即可．【详解】解：∵，∴∠B=∠C=52°，∠BAC=180°-∠B-∠C=180°-52°-52°=76°，由尺规作图痕迹可知：MN垂直平分AB，∴DA=DB，∴∠DAB=∠B=52°，∴∠CAD=∠BAC-∠DAB=76°-52°=24°．故选：B．【点睛】本题考查了线段垂直平分线的尺规作图及等腰三角形的性质等，熟练掌握线段垂直平分线的性质及等腰三角形的性质是解决本类题的关键．5、B【分析】数轴上表示数的点与原点的距离是数的绝对值，根据绝对值的含义可得答案.【详解】解：故选B【点睛】本题考查的是绝对值的含义，掌握“求解一个数的绝对值”是解本题的关键.6、B【分析】由与是位似图形，且知与的位似比是，从而得出周长：周长，由此即可解答．【详解】解：∵与是位似图形，且，与的位似比是．则周长：周长，∵△ABC的周长为2，∴周长故选：B．【点睛】本题考查了位似变换：位似图形的任意一对对应点与位似中心在同一直线上，它们到位似中心的距离之比等于相似比，位似是相似的特殊形式，位似比等于相似比，其对应的周长比等于相似比．7、B【分析】若方程为一元二次方程，则有，，求解；若，方程为一元一次方程，判断有实数根，进而求解取值范围即可．【详解】解：若方程为一元二次方程，则有，解得且若，方程为一元一次方程，有实数根故选B．【点睛】本题考查了一元二次方程根的判别，一元一次方程的根．解题的关键在于全面考虑的情况．8、D【分析】当为各边中点，，，四边形是平行四边形；A中AC=BD，则，平行四边形为菱形，进而可判断正误；B中AC⊥BD，则，平行四边形为矩形，进而可判断正误；E，F，G，H不是各边中点，C中若四点位置满足，则可知四边形EFGH可以是平行四边形，进而可判断正误；D中若四点位置满足，则可知四边形EFGH可以是菱形，进而可判断正误．【详解】解：如图，连接当为各边中点时，可知分别为的中位线∴∴四边形是平行四边形A中AC=BD，则，平行四边形为菱形；正确，不符合题意；B中AC⊥BD，则，平行四边形为矩形；正确，不符合题意；C中E，F，G，H不是各边中点，若四点位置满足，则可知四边形EFGH可以是平行四边形；正确，不符合题意；D中若四点位置满足，则可知四边形EFGH可以是菱形；错误，符合题意；故选D．【点睛】本题考查了平行四边形、菱形、矩形的判定，中位线等知识．解题的关键在于熟练掌握特殊平行四边形的判定．9、B【分析】根据二次函数图象左加右减，上加下减的平移规律进行求解．【详解】解：将抛物线y＝x2先向右平移3个单位长度，得：y＝（x﹣3）2；再向上平移5个单位长度，得：y＝（x﹣3）2+5，故选：B．【点睛】本题考察了二次函数抛物线的平移问题，解题的关键是根据左加右减，上加下减的平移规律进行求解．10、C【分析】根据有理数a，b，c，d在数轴上对应的点的位置，逐个进行判断即可．【详解】解：由有理数a，b，c，d在数轴上对应的点的位置可得，-4＜d＜-3＜-1＜c＜0＜1＜b＜2＜3＜a＜4，∴，，，，故选：C．【点睛】本题考查数轴表示数的意义，根据点在数轴上的位置，确定该数的符号和绝对值是正确判断的前提．二、填空题1、70【分析】如图（见解析），先根据三角形的内角和定理可得，再根据全等三角形的性质即可得．【详解】解：如图，由三角形的内角和定理得：，图中的两个三角形是全等三角形，在它们中，边长为和的两边的夹角分别为和，，故答案为：70．【点睛】本题考查了三角形的内角和定理、全等三角形的性质，熟练掌握全等三角形的性质是解题关键．2、【分析】由，可得且 再求解的值，从而可得答案.【详解】解：，且 解得： 故答案为：【点睛】本题考查的是实数的性质，非负数的性质，求解代数式的值，掌握“绝对值与偶次方的非负性”是解本题的关键.3、-12    -1    ax    9996    【分析】（1）先乘方，再加减即可；（2）逆用积的乘方法则进行计算；（3）运用幂的乘方法则，同底数幂的乘除法法则以及积的乘方法则计算即可；（4）运用平方差公式计算即可．【详解】解：（1）=﹣1+（﹣10）﹣1=﹣1﹣10﹣1=﹣12．故答案为：﹣12．（2）=（）101×（）101（）101=﹣（）101=﹣1．故答案为：﹣1．（3）=a2x﹣2•ax+1÷a2x﹣1=a2x﹣2+x+1﹣（2x﹣1）=ax．故答案为：ax．（4）102×98=（100+2）×（100﹣2）=100²﹣2²=9996．故答案为：9996．【点睛】本题考查了实数的运算，平方差公式，同底数幂的乘除法，幂的乘方与积的乘方，零指数幂，负整数指数幂，熟练掌握各运算法则是解题关键．4、度【分析】根据求出，即可求出旋转角的度数．【详解】解：绕点顺时针旋转得到，则，，故答案为：．【点睛】本题考查了旋转的性质，解题关键是明确旋转角度为的度数．5、【分析】根据线段的垂直平分线的性质得到，，得到和，根据三角形内角和定理计算得到答案．【详解】解：是线段的垂直平分线，，，同理，，，，故答案是：．【点睛】本题考查的是线段的垂直平分线的性质和三角形内角和定理，解题的关键是掌握线段的垂直平分线上的点到线段的两个端点的距离相等．三、解答题1、（1）见解析（2）见解析【分析】（1）根据要求的步骤作角平分线和垂直平分线即可，并连接DE，DF；（2）根据垂直平分线的性质可得，进而证明即可得，进而根据四边相等的四边形是菱形，即可证明四边形是菱形．（1）如图所示，即为所求，（2）证明：如图，设交于点垂直平分在与中四边形是菱形【点睛】本题考查了作角平分线和垂直平分线，菱形的判定，掌握基本作图和菱形的判定定理是解题的关键．2、6【分析】根据公式、及算术平方根的概念逐个求解即可．【详解】解：原式．【点睛】本题考查了、及算术平方根的概念，属于基础题，计算过程中细心即可．3、（1）78个圆圈（2）173【分析】（1）将代入公式求解即可得；（2）先计算当时的值，然后根据题意，第19层从左边数第二个圆圈中的数字即可得出．（1）解：图1中所有圆圈的个数为：，当时，，答：摆放到第12层时，求共用了78个圆圈；（2）先计算当时，，第19层从左边数第二个圆圈中的数字为：，故答案为：173．【点睛】题目主要考查有理数的加法及找规律求代数式的值，理解题意，运用代数式求值是解题关键．4、（1）2xz；（2）ab+1【分析】（1）先计算积的乘方，后自左到右依次计算即可，（2）先计算括号里的，最后计算除法．【详解】解：（1）原式=2xz；（2）原式===ab+1．【点睛】本题考查了整式的混合运算，熟练掌握运算的顺序，运算公式和运算法则是解题的关键．5、（1）（2）或或或（3）【分析】（1）直接利用AB＝计算即可；（2）分两种情况讨论：点B在坐标轴上，设或再利用可得列方程，再解方程即可；（3）直接利用列方程，再解方程即可.（1）解：点A（﹣2，3），B（1，﹣3），则A、B两点间的距离是： 故答案为：（2）解： 点B在坐标轴上，设或 当时，点A（﹣2，3），且A、B两点间的距离是5， 或 或 当时，点A（﹣2，3），且A、B两点间的距离是5， 或 解得： 或（3）解：点A（x，3），B（3，x+1），且A、B两点间的距离是5， 整理得： 解得：【点睛】本题考查的是已知两点坐标求解两点之间的距离，一元二次方程的解法，掌握“两点A（x1，y1）、B（x2，y2），则A、B两点的距离AB＝”是解本题的关键.