【真题汇总卷】2022年北京市海淀区中考数学模拟测评 卷（Ⅰ）（精选）

这是一份【真题汇总卷】2022年北京市海淀区中考数学模拟测评 卷（Ⅰ）（精选），共24页。试卷主要包含了下列计算中正确的是，下列说法正确的是，已知，，且，则的值为等内容，欢迎下载使用。
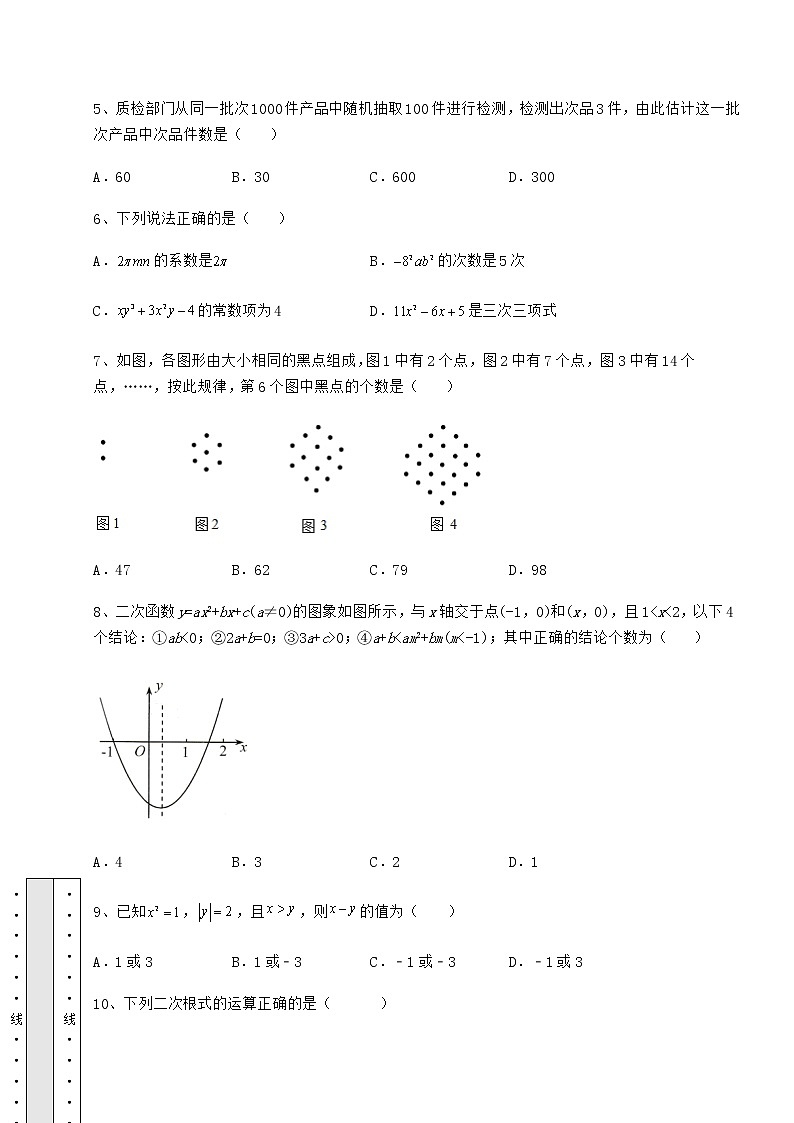
2022年北京市海淀区中考数学模拟测评 卷（Ⅰ） 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、若关于x的不等式组无解，则m的取值范围是（    ）A． B． C． D．2、若关于x，y的方程是二元一次方程，则m的值为（    ）A．﹣1 B．0 C．1 D．23、下列说法正确的是（    ）A．掷一枚质地均匀的骰子，掷得的点数为3的概率是．B．若AC、BD为菱形ABCD的对角线，则的概率为1．C．概率很小的事件不可能发生．D．通过少量重复试验，可以用频率估计概率．4、下列计算中正确的是（    ）A． B． C． D．5、质检部门从同一批次1000件产品中随机抽取100件进行检测，检测出次品3件，由此估计这一批次产品中次品件数是（    ）A．60 B．30 C．600 D．3006、下列说法正确的是（    ）A．的系数是 B．的次数是5次C．的常数项为4 D．是三次三项式7、如图，各图形由大小相同的黑点组成，图1中有2个点，图2中有7个点，图3中有14个点，……，按此规律，第6个图中黑点的个数是（　　）A．47 B．62 C．79 D．988、二次函数y=ax2+bx+c(a≠0)的图象如图所示，与x轴交于点(−1，0)和(x，0)，且1<x<2，以下4个结论：①ab<0；②2a+b=0；③3a+c>0；④a+b<am2+bm(m<−1)；其中正确的结论个数为（    ）A．4 B．3 C．2 D．19、已知，，且，则的值为（    ）A．1或3 B．1或﹣3 C．﹣1或﹣3 D．﹣1或310、下列二次根式的运算正确的是（       ）A． B．C． D．第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、从﹣2，1两个数中随机选取一个数记为m，再从﹣1，0，2三个数中随机选取一个数记为n，则m、n的取值使得一元二次方程x2﹣mx+n＝0有两个不相等的实数根的概率是 _____．2、在平面直角坐标系中，点A坐标为，点B在x轴上，若是直角三角形，则OB的长为______．3、近似数精确到____________位．4、背面完全相同的四张卡片，正面分别写着数字-4，-1，2，3，背面朝上并洗匀，从中随机抽取一张，将卡片上的数字记为，再从余下的卡片中随机抽取一张，将卡片上的数字记为，则点在第四象限的概率为__________．5、当代数式的值为7时，的值为__________．三、解答题（5小题，每小题10分，共计50分）1、（1）计算：．（2）用适当的方法解一元二次方程：．2、计算：3、如图，在⊙O中，弦AC与弦BD交于点P，AC＝BD．（1）求证AP＝BP；（2）连接AB，若AB＝8，BP＝5，DP＝3，求⊙O的半径．4、如图，的长方形网格中，网格线的交点叫做格点．点A，B，C都是格点．请按要求解答下列问题：平面直角坐标系xOy中，点A，B的坐标分别是(－3，1)，(－1，4)，（1）①请在图中画出平面直角坐标系xOy；②点C的坐标是          ，点C关于x轴的对称点的坐标是          ；（2）设l是过点C且平行于y轴的直线，①点A关于直线l的对称点的坐标是          ；②在直线l上找一点P，使最小，在图中标出此时点P的位置；③若Q(m，n)为网格中任一格点，直接写出点Q关于直线l的对称点的坐标（用含m，n的式子表示）．5、已知过点的抛物线与坐标轴交于点A，C如图所示，连结AC，BC，AB，第一象限内有一动点M在抛物线上运动，过点M作交y轴于点P，当点P在点A上方，且与相似时，点M的坐标为______． -参考答案-一、单选题1、D【分析】解两个不等式，再根据“大大小小找不着”可得m的取值范围．【详解】解：解不等式得：，解不等式得：，∵不等式组无解，∴，解得：，故选：D．【点睛】此题主要考查了解不等式组，根据求不等式的无解，遵循“大大小小解不了”原则是解题关键．2、C【分析】根据二元一次方程的定义得出且，再求出答案即可．【详解】解：∵关于x，y的方程是二元一次方程，∴且，解得：m=1，故选C．【点睛】本题考查了二元一次方程的定义，能熟记二元一次方程的定义是解此题的关键．3、B【分析】概率是指事情发生的可能性，等可能发生的事件的概率相同，小概率事件是指发生的概率比较小，不代表不会发生，通过大量重复试验才能用频率估计概率，利用这些对四个选项一次判断即可．【详解】A项：掷一枚质地均匀的骰子，每个面朝上的概率都是一样的都是，故A错误，不符合题意；B项：若AC、BD为菱形ABCD的对角线，由菱形的性质：对角线相互垂直平分得知两条线段一定垂直，则 AC⊥BD 的概率为1是正确的，故B正确，符合题意；C项：概率很小的事件只是发生的概率很小，不代表不会发生，故C错误，不符合题意；D项：通过大量重复试验才能用频率估计概率，故D错误，不符合题意．故选B【点睛】本题考查概率的命题真假，准确理解事务发生的概率是本题关键．4、B【分析】根据绝对值，合并同类项和乘方法则分别计算即可．【详解】解：A、，故选项错误；B、，故选项正确；C、不能合并计算，故选项错误；D、，故选项错误；故选B．【点睛】本题考查了绝对值，合并同类项和乘方，掌握各自的定义和运算法则是必要前提．5、B【分析】根据样本的百分比为，用1000乘以3%即可求得答案．【详解】解：∵随机抽取100件进行检测，检测出次品3件，∴估计1000件产品中次品件数是故选B【点睛】本题考查了根据样本求总体，掌握利用样本估计总体是解题的关键．6、A【分析】根据单项式的系数、次数的定义以及多项式次数、项数、常数项的定义可解决此题．【详解】解：A、的系数是，故选项正确；B、的次数是3次，故选项错误；C、的常数项为-4，故选项错误；D、是二次三项式，故选项错误；故选A．【点睛】本题主要考查单项式的系数、次数的定义以及多项式次数、项数、常数项的定义，熟练掌握单项式的系数、次数的定义以及多项式次数、项数、常数项的定义是解决本题的关键．7、A【分析】根据题意得：第1个图中黑点的个数是 ，第2个图中黑点的个数是 ，第3个图中黑点的个数是，第4个图中黑点的个数是 ，……，由此发现，第 个图中黑点的个数是 ，即可求解．【详解】解：根据题意得：第1个图中黑点的个数是 ，第2个图中黑点的个数是 ，第3个图中黑点的个数是，第4个图中黑点的个数是 ，……，由此发现，第 个图中黑点的个数是 ，∴第6个图中黑点的个数是 ．故选：A【点睛】本题主要考查了图形类规律题，明确题意，准确得到规律是解题的关键．8、B【分析】由开口方向、对称轴的位置可判断结论①；由对称轴的位置可判断结论②；由x=-1函数值为0以及对称轴的位置可判断结论③；由增减性可判断结论④．【详解】解：由图象可知，a>0，b<0，∴ab<0，①正确；因与x轴交于点(−1，0)和(x，0)，且1<x<2，所以对称轴为直线−<1，∴−b<2a，∴2a+b>0，②错误；由图象可知x=−1，y=a−b+c=0，又2a>−b，2a+a+c>−b+a+c，∴3a+c>0，③正确；由增减性可知m<−1，am2+bm+c>0，当x=1时，a+b+c＜0，即a+b<am2+bm，④正确．综上，正确的有①③④，共3个，故选：B．【点睛】本题考查了二次函数图象与系数之间的关系，熟练掌握二次函数的开口方向，对称轴，函数增减性并会综合运用是解决本题的关键．9、A【分析】由题意利用乘方和绝对值求出x与y的值，即可求出x-y的值．【详解】解：∵，， ，∴x=1，y=-2，此时x-y=3；x=-1，y=-2，此时x-y=1．故选：A．【点睛】此题考查了有理数的乘方，绝对值，以及有理数的减法，熟练掌握运算法则是解本题的关键．10、B【分析】根据二次根式的性质及运算逐项进行判断即可．【详解】A、，故运算错误；B、，故运算正确；C、，故运算错误；D、，故运算错误．故选：B【点睛】本题考查了二次根式的性质、二次根式的运算，掌握二次根式的性质及运算法则是关键．二、填空题1、【分析】先画树状图列出所有等可能结果，从中找到使方程有两个不相等的实数根，即m＞n的结果数，再根据概率公式求解可得．【详解】解：画树状图如下：由树状图知，共有12种等可能结果，其中能使方程x2-mx+n=0有两个不相等的实数根，即m2-4n＞0，m2＞4n的结果有4种结果，∴关于x的一元二次方程x2-mx+n=0有两个不相等的实数根的概率是，故答案为：．【点睛】本题是概率与一元二次方程的根的判别式相结合的题目．正确理解列举法求概率的条件以及一元二次方程有根的条件是关键．2、4或【分析】点B在x轴上，所以 ，分别讨论， 和两种情况，设 ，根据勾股定理求出x的值，即可得到OB的长．【详解】解：∵B在x轴上，∴设 ，∵ ，∴ ，①当时，B点横坐标与A点横坐标相同，∴ ，∴ ，∴ ，②当时， ，∵点A坐标为，，∴ ，∴ ，解得： ，∴ ，∴ ，故答案为：4或．【点睛】本题考查平面直角坐标系中两点间距离以及勾股定理，分情况讨论是解题关键．3、百【分析】一个近似数的有效数字是从左边第一个不是0的数字起，后面所有的数字都是这个数的有效数字．【详解】解：∵104是1万，6位万位，0为千位，5为百位，∴近似数6.05×104精确到百位；故答案为百．【点睛】此题考查近似数与有效数字，解题关键在于掌握从左边第一个不是0的数开始数起，到精确到的数位为止，所有的数字都叫做这个数的有效数字．最后一位所在的位置就是精确度．4、【分析】第四象限点的特征是，所以当横坐标只能为2或3，纵坐标只能是或，画出列表图或树状图，算出满足条件的情况，进一步求得概率即可．【详解】如下图： -4-123-4  -1   2   3  ∵第四象限点的坐标特征是，∴满足条件的点分别是： ，共4种情况，又∵从列表图知，共有12种等可能性结果，∴点在第四象限的概率为．故答案为：【点睛】本题主要考察概率的求解，要熟悉树状图或列表图的要点是解题关键．5、2【分析】由条件可得，而，从而可求得结果的值．【详解】解：∵，∴，∴．故答案为：2．【点睛】本题是求代数式的值，关键是由条件求得，运用了整体思想．三、解答题1、（1）2+；（2），【分析】（1）先计算零指数幂，分母有理化，负指数幂，特殊三角函数值，再合并同类项即可；（2）因式分解法解一元二次方程．【详解】（1）解：，，，；（2）解：原方程分解因式得， 或，解得，．【点睛】本题考查含有锐角三角函数的实数混合运算，零指数幂，负指数幂，二次根式分母有理化，一元二次方程的解法，掌握含有锐角三角函数的实数混合运算，零指数幂，负指数幂，二次根式分母有理化，一元二次方程的解法．2、【分析】先根据绝对值的意义、负整数指数幂的性质、二次根式的化简和零指数幂分别化简，再计算即可.【详解】解：原式【点睛】此题考查了实数的混合运算，掌握相应的运算性质和运算法则是解答此题的关键.3、（1）证明见解析；（2）．【分析】（1）连接，先证出，再根据圆周角定理可得，然后根据等腰三角形的判定即可得证；（2）连接，并延长交于点，连接，过作于点，先根据线段垂直平分线的判定与性质可得，再根据线段的和差、勾股定理可得，然后根据直角三角形全等的判定定理证出，根据全等三角形的性质可得，最后在中，利用勾股定理可得的长，从而可得的长，在中，利用勾股定理即可得．【详解】证明：（1）如图，连接，，，，即，，；（2）连接，并延长交于点，连接，过作于点，，，是的垂直平分线，，，，，在和中，，，，设，则，在中，，即，解得，在中，，即的半径为．【点睛】本题考查了圆周角定理、直角三角形全等的判定定理与性质、勾股定理、垂径定理等知识点，较难的是题（2），通过作辅助线，构造全等三角形和直角三角形是解题关键．4、（1）作图见解析，（1，2），（1，-2）；（2）①（5，1）；②P点位置见解析；③（2-m，n）【分析】（1）由A、B点坐标即可知x轴和y轴的位置，即可从图像中得知C点坐标，而的横坐标不变，纵坐标为C点纵坐标的相反数．（2）由C点坐标（1，2）可知直线l为x=1①点是点A关于直线l的对称点，由横坐标和点A横坐标之和为2，纵坐标不变，即可求得坐标为（5，1）．②由①可得点A关于直线l的对称点，连接B交l于点P，由两点之间线段最短即可知点P为所求点．③设点Q（m，n）关于l的对称点为（x，y），则有（m+x）÷2=1，y=n，即可求得对称点（2-m，n）【详解】（1）平面直角坐标系xOy如图所示由图象可知C点坐标为（1，2）点是 C点关于x轴对称得来的则的横坐标不变，纵坐标为C点纵坐标的相反数即点坐标为（1，-2）．（2）如图所示，由C点坐标（1，2）可知直线l为x=1①A点坐标为（-3，1），关于直线x=1对称的坐标横坐标与A点横坐标坐标和的一半为1，纵坐标不变则为坐标为（5，1）②连接①所得B，B交直线x=1于点P由两点之间线段最短可知为B时最小又∵点是点A关于直线l的对称点∴∴为B时最小故P即为所求点．③设任意格点Q（m，n）关于直线x=1的对称点为（x，y）有（m+x）÷2=1，y=n即x=2-m，y=n则纵坐标不变，横坐标为原来横坐标相反数加2即对称点坐标为（2-m，n）．【点睛】本题考查了坐标轴中的对称点问题，熟悉坐标点关于轴对称的坐标变换，结合图象运用数形结合思想是解题的关键．5、或【分析】运用待定系数法求出函数关系式，求出点A，C的坐标，得出AC=，BC=，AB=，判断为直角三角形，且， 过点M作MG⊥y轴于G，则∠MGA=90°，设点M的横坐标为x，则MG=x，求出含x的代数式的点M的坐标，再代入二次函数解析式即可．【详解】把点B (4，1)代入，得：∴ 抛物线的解析式为令x=0，得y=3，∴A(0，3)令y=0，则解得， ∴C（3，0）∴AC=∵B（4，1）∴BC=，AB= ∴ ∴为直角三角形，且，过点M作MG⊥y轴于G，则∠MGA=90°，设点M的横坐标为x，由M在y轴右侧可得x＞0，则MG=x，∵PM⊥MA，∠ACB=90°，∴∠AMP=∠ACB=90°，①如图，当∠MAP=∠CBA时，则△MAP∽△CBA，∴ 同理可得， ∴ ∴AG=MG=x，则M（x，3+x），把M（x，3+x）代入y=x2-x+3，得x2-x+3=3+x，解得，x1=0（舍去），x2=，∴3+x=3+ ∴M（，）；②如图，当∠MAP=∠CAB时，则△MAP∽△CAB，∴同理可得，AG=3MG=3x，则P（x，3+3x），把P（x，3+3x）代入y=x2-x+3，得x2-x+3=3+3x，解得，x1=0（舍去），x2=11，∴M（11，36），综上，点M的坐标为（11，36）或（，）【点睛】本题考查了待定系数法求解析式，相似三角形的判定与性质等等知识，解题关键是注意分类讨论思想在解题过程中的运用．