华师大版八年级下册2. 函数的图象优秀教学设计

这是一份华师大版八年级下册2. 函数的图象优秀教学设计，共6页。
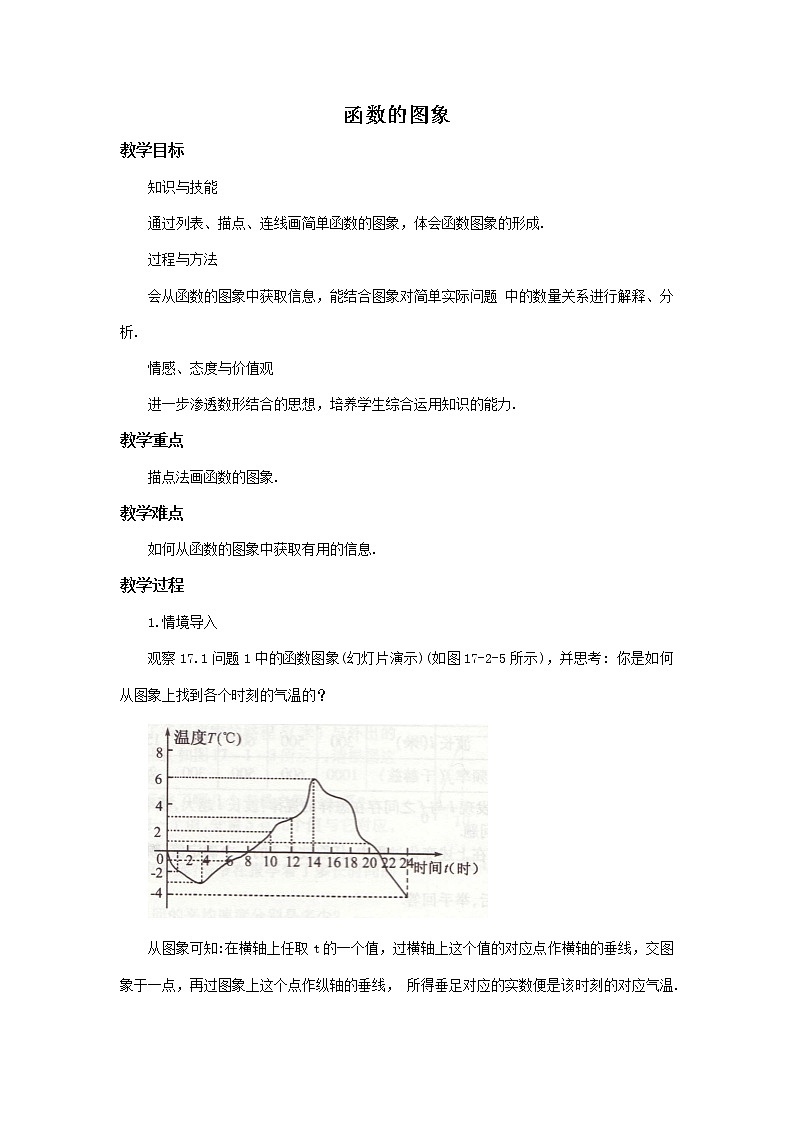
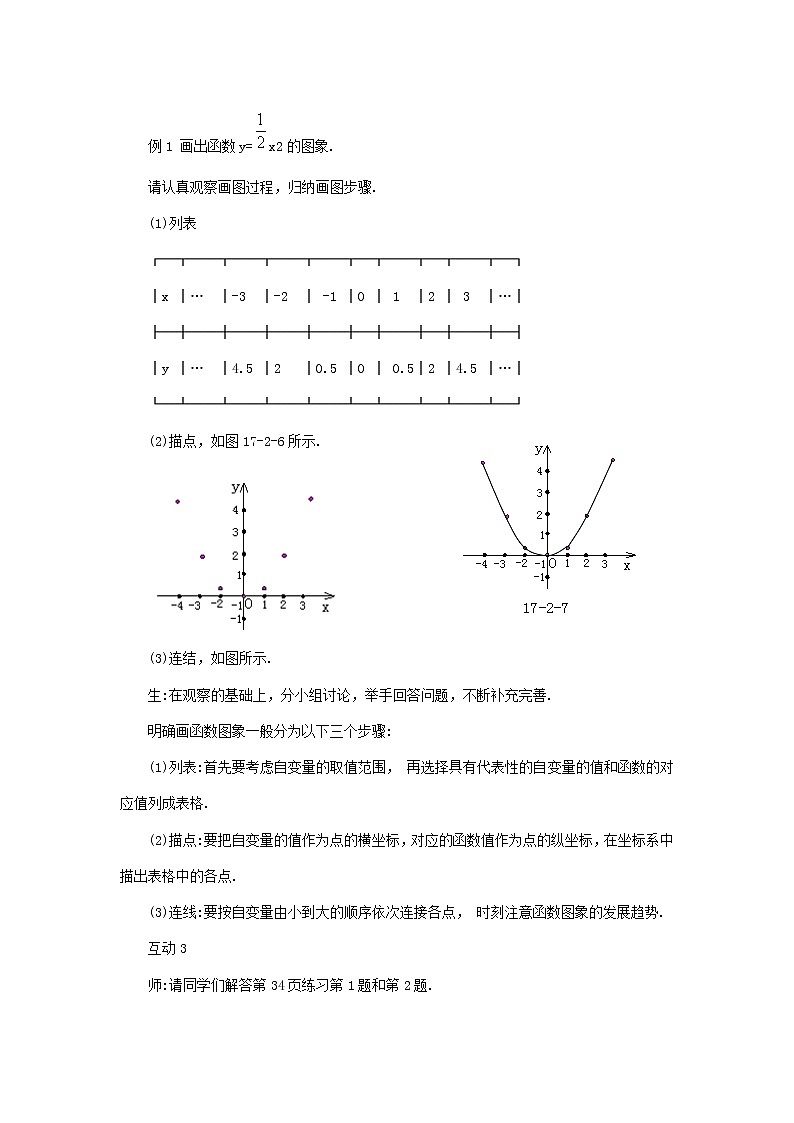
函数的图象教学目标知识与技能[来源:中@国教育&*出#版网~]通过列表、描点、连线画简单函数的图象，体会函数图象的形成.过程与方法[中^国教育~@出*版网#]会从函数的图象中获取信息，能结合图象对简单实际问题 中的数量关系进行解释、分析.情感、态度与价值观进一步渗透数形结合的思想，培养学生综合运用知识的能力. 教学重点描点法画函数的图象.教学难点如何从函数的图象中获取有用的信息.[来源:z@z#step.&co%m*]教学过程1.情境导入观察17.1问题1中的函数图象(幻灯片演示)(如图17-2-5所示)，并思考:你是如­何从图象上找到各个时刻的气温的？从图象可知:在横轴上任取t的一个值，过横轴上这个值的对应点作横轴的垂线­，交图象于一点，再过图象上这个点作纵轴的垂线，所得垂足对应的实数便是该时刻­的对应气温.所有满足这种条件的点的集合，便构成了该函数的图象.2.课前热身给定一个函数，如何确定它的自变量的取值范围？取自变量(允许)的一个固定值­，如何求出对应的函数值？取函数的一个固定值，如何求出对应的自变量的值？[来源~&:中教^@%网]3.合作探究(1)整体感知通过前面知识的学习，我们对函数的图象已经有了初步的感性认识，本节课我们­将着重系统研究函数图象的意义、函数图象的一般画法，进一步探讨通过观察图象­解答提出的问题.[中国^教&育*出@版~网](2)四边互动互动1师:利用多媒体演示.已知函数y=x，请按下列要求进行操作.(1)取自变量x的一个值，算出函数对应值y，分别以自变量的值和函数的对应值­作为点的横坐标和纵坐标，在坐标系中描出这个点；(2)重复上述操作过程，描出10个不同的点；[来源:zzs@te%p#&.co^m](3)结果你发现了什么？生:动手操作，交流发现的结论.明确通过观察发现:这些点在经过原点的同一条直线上，如果无限地描出符合­条件的点，这些点就构成了这条直线──这条直线就是y=x函数的图象.归纳可知:给定一个函数，取自变量的一个值，算出函数的对应值，分别以该自变­量的值和对应的函数值作为点的横坐标和纵坐标，在坐标系中描出这个点，那么所有­这样的点的集合构成的图形就是该函数的图象.互动2师:利用多媒体演示“画函数图象”课件(华东师大出版社教学光盘).例1 画出函数y=x2的图象.请认真观察画图过程，归纳画图步骤.(1)列表┌─┬──┬──┬──┬──┬─┬──┬─┬──┬─┐│x │…  │-3  │-2  │ -1 │0 │ 1  │2 │ 3  │…│├─┼──┼──┼──┼──┼─┼──┼─┼──┼─┤[中国*教育%出&版#网@]│y │…  │4.5 │2   │0.5 │0 │ 0.5│2 │4.5 │…│└─┴──┴──┴──┴──┴─┴──┴─┴──┴─┘[来#%源:中国教育&出版网^@](2)描点，如图17-2-6所示.(3)连结，如图所示.生:在观察的基础上，分小组讨论，举手回答问题，不断补充完善.明确画函数图象一般分为以下三个步骤:(1)列表:首先要考虑自变量的取值范围，再选择具有代表性的自变量的值和函数的对应值列成表格.(2)描点:要把自变量的值作为点的横坐标，对应的函数值作为点的纵坐标，在坐标系中描出表格中的各点.(3)连线:要按自变量由小到大的顺序依次连接各点，时刻注意函数图象的发展趋势.互动3[中国~教&^育出@*版网]师:请同学们解答第34页练习第1题和第2题.生:独立尝试，然后在小组间交流.明确  教师利用多媒体演示操作的结果，并说明第2题图象断裂的原因(自变量­的值不能为0).互动4师:利用多媒体演示幻灯片(问题1).例2 王教授和孙子小强经常一起进行早锻炼，主要活动是爬山.有一天，小强让爷爷­先上，然后追赶爷爷，两人都爬上了山顶.图17-2-8中两条线段分别表示小强和爷爷­离开山脚的距离(米)与爬山的时间(分)的关系(从小强开始爬山时计时)，看图回答下列问题:(1)小强让爷爷先上多少米？(2)山顶离山脚的距离有多少米？谁先爬上山顶？(3)谁的速度大？大多少？(精确到米)生:思考后，逐个举手回答，不断补充完善.明确由图象可知:小强出发0分钟时，爷爷已经爬山60米，因此小强让爷爷先上60米；山顶离山脚的距离是300米，小强先爬上山；小强爬山300米用了10分钟，速度为30米/分，爷爷爬山(300-60)米=240米，用了11分钟，速度约为22米/分，因此小强的速度大，大8米/分.互动5师:利用多媒体演示“高尔夫球里的数字”课件(问题2)(华东师范大学出版社­教学光盘).王强在电脑上进行高尔夫球的模拟练习，在某处按函数关系式y= 击球，球正好­进洞.其中，y(m)是球的飞行高度，x(m)是球飞出的水平距离.[中^%&国#教育@出版网](1)试画出高尔夫球飞行的路线；[ww@w.#zzstep.~^com*](2)从图象上看，高尔夫球的最大飞行高度是多少？球的起点与洞之间的距离是­多少？解:(1)列表如下:─┬─┬──┬─┬─┬─┬─┬─┬─┬──[来源:#中^@教网*&]x │0 │1   │2 │3 │4 │5 │6 │ 7│8[中~国%&*教育出^版网]─┼─┼──┼─┼─┼─┼─┼─┼─┼──y │0 │1.4 │  │  │  │  │  │  │[来源:中*~国教%@育出版网^]─┴─┴──┴─┴─┴─┴─┴─┴─┴──在如图17-2-9所示的直角坐标系中，描点、连线，便可得到这个函数的大致图象.       (2)从图象上看，高尔夫球的最大飞行高度是3.2m，球的起点与洞之间的距离是8m.[来~*@源:中国教育出^版#网]生:按课本的要求完成填表、画图、填空，相互交流操作的结果.明确利用课件验证同学们操作的结果.列表中取自变量的值时，应考虑使实际有意义(上述函数自变量取值不能小于0­，也不能大于9)；连线时，画出的图象不能超出自变量的限制的区域.4.学习小结[来源&~:*zzstep.co@m%](1)内容总结函数图象      意义──符合某种条件的所有点的集合构成的图形              画法──列表、描点、连线(2)方法归纳画函数图象应注意的几个问题:列表时应考虑自变量的取值范围，在自变量的允­许范围内选择具有代表性的自变量的几个值列成表格；在描点时不能把横、纵坐标­的位置颠倒；连线时应考虑图象的发展趋势和局限区域.(三)拓展延伸1.链接生活李丹家距学校m千米，一天她从家上学先以a千米/时的速度跑步锻炼前进，后以­匀速b千米/时步行到达学校，共用n小时.图17-2-12中能够反映李丹同学距学校的距­离s(千米)与上学的时间t(小时)之间的大致图象是(C)                            图17-2-122.实践探索(1)实践活动收集利用函数图象解决现实生活问题的实例.