初中第25章 投影与视图综合与测试课后复习题

沪科版九年级数学下册第25章投影与视图课时练习

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、如图所示的几何体，它的左视图是（    ）

A． B． C． D．

2、如图，小明在A时测得某树的影长为8m，B时又测得该树的影长为2m，若两次日照的光线互相垂直，则树的高度为（　　）m．

A．2 B．4 C．6 D．8

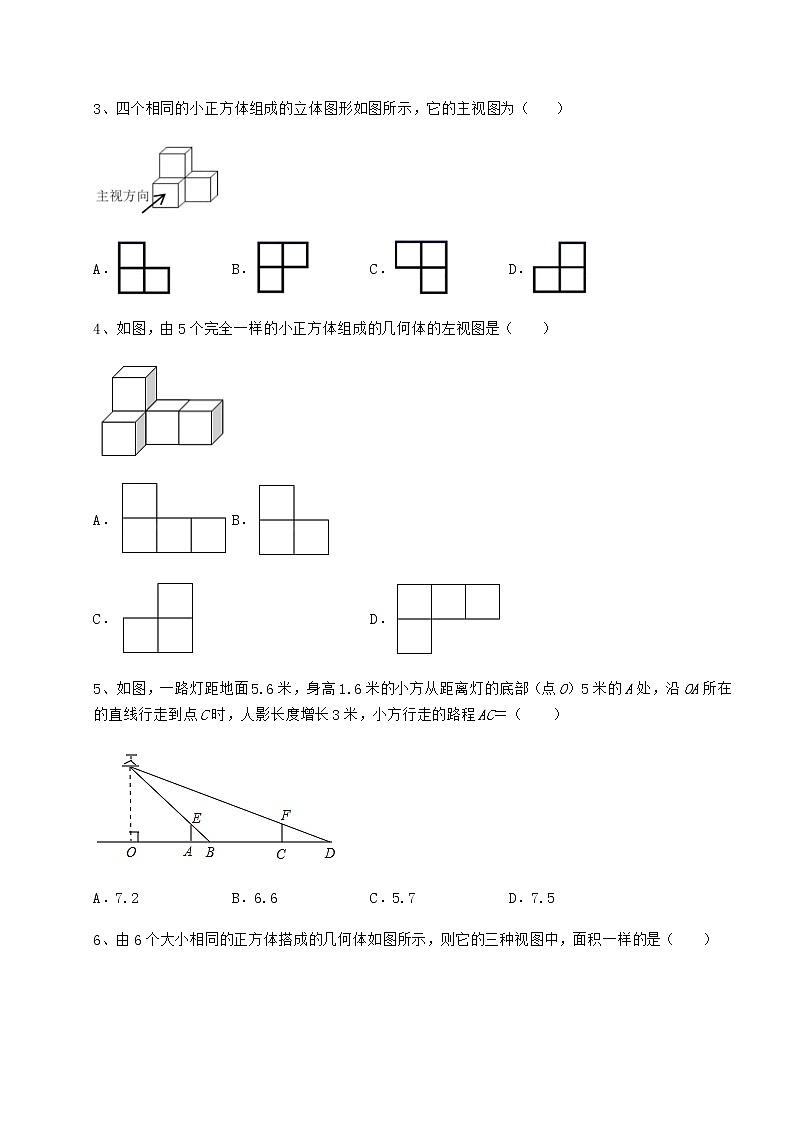
3、四个相同的小正方体组成的立体图形如图所示，它的主视图为（    ）

A． B． C． D．

4、如图，由5个完全一样的小正方体组成的几何体的左视图是（    ）

A． B． 

C．  D．

5、如图，一路灯距地面5.6米，身高1.6米的小方从距离灯的底部（点O）5米的A处，沿OA所在的直线行走到点C时，人影长度增长3米，小方行走的路程AC＝（　　）

A．7.2 B．6.6 C．5.7 D．7.5

6、由6个大小相同的正方体搭成的几何体如图所示，则它的三种视图中，面积一样的是（    ）

A．主视图与俯视图 B．主视图与左视图

C．俯视图与左视图 D．主视图、左视图和俯视图

7、中国有悠久的金石文化，印信是金石文化的代表之一．南北朝时期的官员独孤信的印信是迄今发现的中国古代唯一一枚楷书印．它的表面均由正方形和等边三角形组成（如图1），可以看成图2所示的几何体．从正面看该几何体得到的平面图形是（    ）

A． B． C． D．

8、如图是由5个小立方块搭成的几何体，则该几何体从左面看到的形状图是（    ）

A． B．

C． D．

9、如图所示的几何体的左视图为（　　）

A． B． C． D．

10、如图，该几何体的俯视图是（    ）

A．  B．

C．  D．

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、如图所示是某种型号的正六角螺母毛坯的三视图，则左视图的面积为_________．

2、如图是某圆柱体果罐，它的主视图是边长为的正方形，该果罐侧面积为_____．

3、如图是某物体的三视图，则此物体的体积为_____（结果保留π）．

4、用小立方块搭一几何体，它的主视图和俯视图如图所示，这个几何体最少要_____个立方块，最多要______个立方块．

5、根据三视图，这个几何体的侧面积是 ___．

三、解答题（5小题，每小题10分，共计50分）

1、如图是一个由几个小正方块所搭成的几何体从上面看到的形状图，每个小正方形边长为1，小正方形中的数字表示在该位置的小正方块的个数，请在右边的方格中画出这个几何体从正面和左面看到的形状图，并求出这个几何体的表面积．

2、一个几何体的三种视图如图所示．

（1）这个几何体的名称是____；

（2）求这个几何体的表面积；

（3）求这个几何体的体积．

3、请从正面、左面、上面观察， 画出该几何体的三视图

4、如图是由7个相同的小立方块搭成的几何体．请画出主视图、左视图和俯视图．

5、如图所示是一个用小立方体搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方体的个数，请你画出它的主视图与左视图．

-参考答案-

一、单选题

1、D

【分析】

左视图：从物体左面所看的平面图形，注意：看到的棱画实线，看不到的棱画虚线，据此进行判断即可．

【详解】

解：如图所示，几何体的左视图是：

故选：D．

【点睛】

本题考查简单组合体的三视图，正确掌握观察角度是解题关键．

2、B

【分析】

根据题意，画出示意图，易得：△EDC∽△FDC，进而可得，即DC2＝ED•FD，代入数据可得答案．

【详解】

解：根据题意，作△EFC，树高为CD，且∠ECF＝90°，ED＝2m，FD＝8m；

∵∠E+∠F＝90°，∠E+∠ECD＝90°，

∴∠ECD＝∠F，

∴△EDC∽△FDC，

∴，即DC2＝ED•FD＝2×8＝16，

解得CD＝4m．

故选：B．

【点睛】

本题主要考查了平行投影与相似三角形的应用，准确计算是解题的关键．

3、A

【分析】

根据几何体的三视图解答即可．

【详解】

根据立体图形得到：

主视图为：，

左视图为：，

俯视图为：，

故选：

【点睛】

本题考查了三视图的知识，主视图是从物体的正面看得到的视图．

4、B

【分析】

根据从左边看得到的图形是左视图，可得答案．

【详解】

解：从从左边看有2列两层，2列从左到右分别有2、1个小正方形，

故选：B．

【点睛】

本题考查了简单组合体的三视图，解题的关键是从左边看得到的图形是左视图．

5、D

【分析】

设出影长AB的长，利用相似三角形可以求得AB的长，然后在利用相似三角形求得AC的长即可．

【详解】

解：∵AE⊥OD，OG⊥OD，

∴AE//OG，

∴∠AEB=∠OGB，∠EAB=∠GOB，

∴△AEB∽△OGB，

∴，即 ，

解得：AB＝2m；

∵OA所在的直线行走到点C时，人影长度增长3米，

∴DC＝AB+3=5m，OD=OA+AC+CD=AC+10，

∵FC∥GO，

∴∠CFD=∠OGD，∠FCD=∠GOD，

△DFC∽△DGO，

∴，

即，

解得：AC＝7.5m．

所以小方行走的路程为7.5m．

故选择：D．

【点睛】

本题主要考查的是相似三角形在实际中的中心投影的应用，掌握相似三角形判断与性质，利用对应边成比例是解答本题的关键．

6、B

【分析】

根据简单几何体的三视图解答即可．

【详解】

解：该几何体的三视图如图所示：

，  ，

由三视图可知，面积一样的是主视图与左视图，

故选：B．

【点睛】

本题考查简单几何体的三视图，熟知三视图的特点是解答的关键．

7、D

【分析】

找到从正面看所得到的图形即可．

【详解】

解：从正面看是一个正六边形，里面有2个矩形，

故选D．

【点睛】

本题灵活考查了三种视图之间的关系以及视图和实物之间的关系，同时还考查了对图形的想象力，难度适中．

8、D

【分析】

左视图：从左边看立体图形，看到的平面图形是左视图，根据左视图的定义可得答案.

【详解】

解：该几何体从左面看到的形状图有2列，

第1列看到1个正方形，第2列看到2个正方形，

所以左视图是D，

故选D

【点睛】

本题考查的是三视图，值得注意的是能看到的立体图形中的线条都要画成实线，看不到的画成虚线，掌握“左视图的含义”是解题的关键.

9、C

【分析】

找到从左边看所得到的图形即可，注意所有看得到的棱用实线表示，看不到的部分用虚线表示

【详解】

解：从左边看到的图形是：

故选C

【点睛】

本题考查了简单组合体的三视图，理解看不到的且存在的是虚线解题的关键．

10、A

【分析】

俯视图，从上面看到的平面图形，根据定义可得答案.

【详解】

解：从上面看这个几何体看到的是三个长方形，

所以俯视图是：

故选A

【点睛】

本题考查的是三视图，注意能看到的棱都要画成实线，掌握“三视图中的俯视图”是解本题的关键.

二、填空题

1、

【分析】

如图，连接过作于再求解 再确定左视图是长方形，两边分别为3cm，cm，从而可得答案.

【详解】

解：如图，连接过作于

由俯视图可得：

由主视图可得：正六角螺母毛坯的高为：3cm，

左视图的面积为

故答案为：

【点睛】

本题考查的是三视图，左视图的面积的计算，掌握“左视图是长方形”是解本题的关键.

2、

【分析】

根据圆柱体的主视图为边长为10cm的正方形，得到圆柱的底面直径和高，从而计算侧面积．

【详解】

解：∵果罐的主视图是边长为10cm的正方形，为圆柱体，

∴圆柱体的底面直径和高为10cm，

∴侧面积为=，

故答案为：．

【点睛】

本题考查了几何体的三视图，解题的关键是根据三视图得到几何体的相关数据．

3、π

【分析】

由已知中的三视图，可以判断出该物体是由下部分为底面直径为10、高10的圆柱，上部分是底面直径为10，高为5的圆锥组成的，代入圆柱、圆锥的体积公式，即可得到答案．

【详解】

解：由三视图知，该物体是由下部分为底面直径为10、高10的圆柱，上部分是底面直径为10，高为5的圆锥组成的．

∴体积＝V圆柱+V圆锥＝．

故答案为：π．

【点睛】

本题考查的知识点是由三视图还原实物图，圆柱和圆锥的体积，其中根据三视图准确分析出几何体的形状及底面半径、高等关键数据是解答本题的关键．

4、       

【分析】

依据主视图可得俯视图中各位置小正方体的个数，进而得到这个几何体中正方体最少和最多的个数．

【详解】

由主视图可得，这个几何体（第2列，第3列组合不唯一）最少要1+3+4=8个立方块；

由主视图可得，这个几何体最多要1+4+6=11个立方块；

故答案为：8，11．

【点睛】

本题主要考查三视图判断几何体，解题时应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．

5、200π

【分析】

根据三视图确定几何体为圆柱，侧面积为2πrh，结合主视图确定h，结合俯视图确定底面圆的直径，计算即可．

【详解】

∵，

∴几何体为圆柱，且圆柱的高为h=20，底面圆的直径为10，

∴侧面积为2πrh=10×20×π=200π．

故答案为：200π．

【点睛】

本题考查了几何体的三视图，结合体侧面积计算，熟练掌握常见几何体的三视图及其侧面积计算公式是解题的关键．

三、解答题

1、图见解析，28

【分析】

从正面看有三列，看到的正方形的个数分别为1，3，1，从左边看有两列，看到的正方形的个数分别为2，3，从而可画出主视图与左视图，再根据三种视图看到的正方形的数量乘以2，从而可计算表面积.

【详解】

解：从正面和左面看到的形状图如下图

表面积

【点睛】

本题考查的是根据俯视图还原几何体，同时考查画正视图与左视图，几何体的表面积，掌握三种视图的含义是解题的关键.

2、（1）圆柱体；（2）这个几何体的表面积为；（3）这个几何体的体积为．

【分析】

（1）根据这个几何体的三视图即可求解；

（2）根据三视图可得到圆柱的高为6，底面半径为2，然后根据圆柱的表面积等于侧面积加两个底面积求解即可；

（3）根据圆柱的体积等于底面积×高求解即可．

【详解】

解：（1）由图可得，主视图是长方形，左视图是长方形，俯视图是圆，

∴这个几何体是圆柱体，

故答案是：圆柱体；

（2）由三视图可得，圆柱的高为6，底面半径为2，

∴这个圆柱的表面积＝底面积×2+侧面积＝；

（3）这个圆柱的体积＝底面积×高＝．

【点睛】

此题考查了几何体的三视图，求圆柱的表面积和体积，解题的关键是熟练掌握三视图的表示方法以及圆柱的表面积和体积公式．

3、见解析

【分析】

根据主视图的定义画出从前面先后看得到的图形，根据左视图的定义画出从左向右看得到的图形，根据俯视图的定义画出从上向下看得到的图形即可．

【详解】

解：主视图是从前面先后看得到的图形，图形分三列，左边列有三层3个小正方形，中间列一层1个小正方形，右边列有两层2个小正方形，根据看到的图形可画出主视图，

左视图是从左向右看得到的图形，图形分三列，左边列左边列有三层3个小正方形，中间列两层2个小正方形，右边列有一层1个小正方形，根据看到的图形可画出左视图，

俯视图是从上向下看得到的图形，图形分三列，上对齐，左边列有3个小正方形，中间列2个小正方形，右边列有1个小正方形，根据看到的图形可画出俯视图．

【点睛】

本题考查简单组合体的三视图，掌握三视图的定义是解题关键．

4、见解析

【分析】

主视图有3列，每列小正方形数目分别为2，1，3；左视图有2列，每列小正方形数目分别为3，2；俯视图有3列，每列小正方形数目分别为2，1，1．

【详解】

解：如图所示，

【点睛】

本题考查作图—三视图，主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形．

5、见解析

【分析】

根据简单组合体的三视图的意义和画法画出相应的图形即可．

【详解】

这个组合体的三视图如下：

【点睛】

本题考查简单组合体的三视图，理解视图的定义，掌握简单组合体三视图的画法是正确解答的关键．