天津市实验中学滨海学校2020-2021学年高二下学期期中考试数学试题（黄南民族班）（含答案）

2020-2021年度第二学期高二年级期中质量调查（数学）试卷

 满分：150分  时长：100分钟

一、单选题（本题共12小题，每小题5分，共60分）

1．在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X表示这10个村庄中交通不方便的村庄数，则下列概率中等于的是（    ）

A．P(X＝2) B．P(X≤2)

C．P(X＝4) D．P(X≤4)

2．已知随机变量，且，则（    ）

A． B．8 C．12 D．24

3．设A，B为两个事件，已知P(B)=0.4，P(A)=0.5 ，P(B|A)=0.3 ，则P()=（    ）

A．0.3 B．0.4 C．0.5 D．0.6

4．蟋蟀鸣叫可以说是大自然优美、和谐的音乐，殊不知蟋蟀鸣叫的频率x（每分钟鸣叫的次数）与气温y（单位：℃）存在着较强的线性相关关系．某地观测人员根据下表的观测数据，建立了y关于x的线性回归方程，

则当蟋蟀每分钟鸣叫56次时，该地当时的气温预报值为（    ）

A．33℃ B．34℃ C．35℃ D．35.5℃

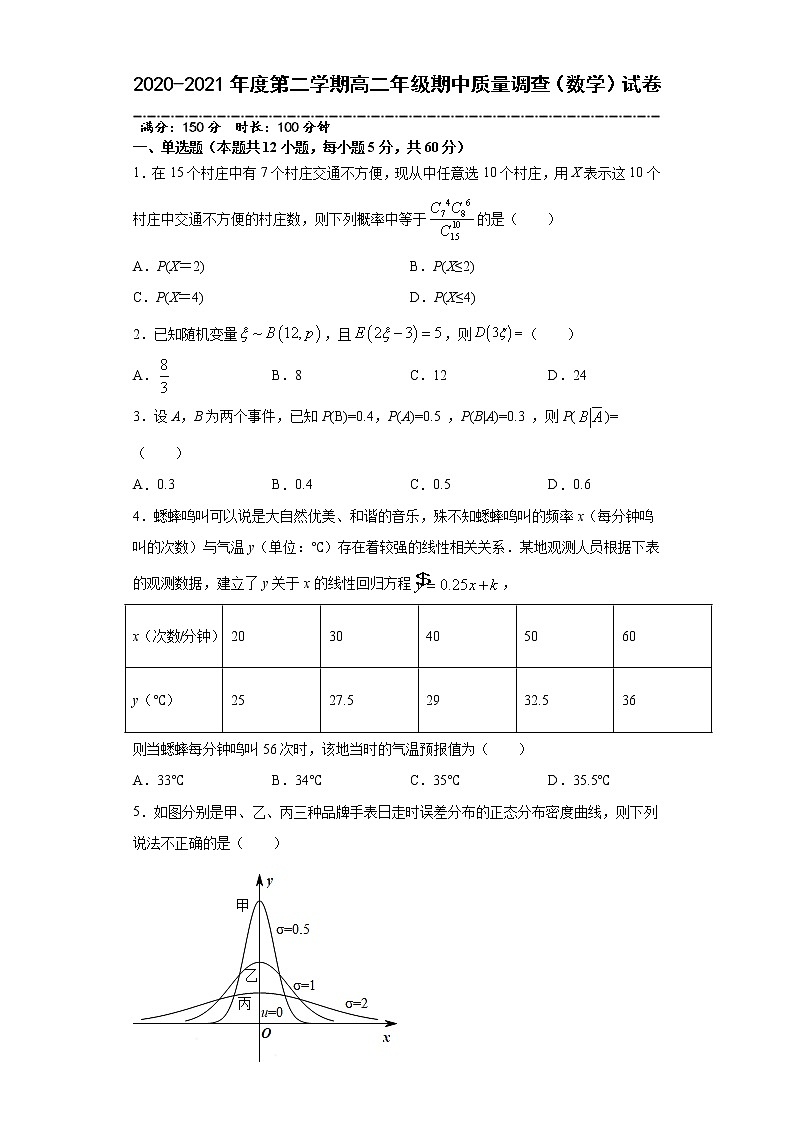
5．如图分别是甲、乙、丙三种品牌手表日走时误差分布的正态分布密度曲线，则下列说法不正确的是（    ）

A．三种品牌的手表日走时误差的均值相等

B．三种品牌的手表日走时误差的均值从大到小依次为甲、乙、丙

C．三种品牌的手表日走时误差的方差从小到大依次为甲、乙、丙

D．三种品牌手表中甲品牌的质量最好

6．我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“─”和阴爻“--”，如图就是一重卦.在所有重卦中随机取一重卦，记事件“取出的重卦中至少有2个阴爻”，事件“取出的重卦中恰有3个阳爻”.则（    ）

A． B． C． D．

7．下列说法正确的是（    ）

①独立性检验的基本思想是带有概率性质的反证法;②独立性检验就是选取一个假设H0条件下的一个小概率事件,若在一次试验中该事件发生了,这是与实际推断相抵触的"不合理"现象,则作出拒绝H0的推断;③独立性检验一定能给出明确的结论.

A．①②.

B．①③.

C．②③.

D．①②③.

8．已知函数，则其大致图象为（    ）

A． B．

C． D．

9．已知函数在处取得极大值10，则的值为（    ）

A． B．－2 C．－2或 D．2或

10．已知二项式，且，则

A． B． C． D．

11．已知关于x的方程在上有两解，则实数k的取值范围为（    ）

A． B． C． D．

12．若对任意的，，，恒成立，则a的最小值为（    ）

A． B． C． D．

二、填空题（本题共6小题，每小题5分，共30分）

13．计算：______．

14．辛丑牛年春晚现场请来了荣获“人民英雄”“时代楷模”“全国道德模范”称号的几位先进人物代表共度新春佳节，他们是“人民英雄”陈薇，“时代楷模”毛相林、张连刚，林占禧，“全国道德模范”张晓艳、周秀芳、张家丰，朱恒银，从中选出两位荣誉称号不同的代表先后给全国人民拜年，则不同的发言情况有__________种.

15．已知函数的导函数为，且满足，则___________.

16．一个袋中装有10个大小相同的黑球、白球和红球．已知从袋中任意摸出2个球，至少得到一个白球的概率是，则袋中的白球个数为_____，若从袋中任意摸出3个球，记得到白球的个数为ξ，则随机变量ξ的数学期望Eξ＝_____．

17．展开式中，的系数为______．

18．已知是定义域为R的奇函数，是的导函数，，当时，，则关于x的不等式解集为____________.

三、解答题（本题共4小题，17题14分，18题、19题15分，20题16分，共60分）

19．已知函数，其中，

（1）若曲线在点处的切线方程为，求函数的解析式

（2）讨论函数的单调性

20．设函数的导数满足，.

（1）求的单调区间；

（2）在区间上的最大值为20，求的值.

（3）若函数的图象与轴有三个交点，求的范围.

21．高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型，在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，前面挡有一块玻璃，让一个小球从高尔顿板上方的通道口落下，小球在下落的过程中与层层小木块碰撞，且等可能向左或向右滚下，最后掉入高尔顿板下方的某一球槽内.如图1所示的高尔顿板有7层小木块，小球从通道口落下，第一次与第2层中间的小木块碰撞，以的概率向左或向右滚下，依次经过6次与小木块碰撞，最后掉入编号为1，2，…，7的球槽内.例如小球要掉入3号球槽，则在6次碰撞中有2次向右4次向左滚下.

（1）如图1，进行一次高尔顿板试验，求小球落入5号球槽的概率；

（2）小红､小明同学在研究了高尔顿板后，利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图1所示的高尔顿板，付费6元可以玩一次游戏，小球掉入m号球槽得到的奖金为元，其中.小明改进了高尔顿板(如图2)，首先将小木块减少成5层，然后使小球在下落的过程中与小木块碰撞时，有的概率向左，的概率向右滚下，最后掉入编号为1，2，……，5的球槽内，改进高尔顿板后只需付费4元就可以玩一次游戏，小球掉入n号球槽得到的奖金为元，其中.两位同学的高尔顿板游戏火爆进行，很多同学参加了游戏，你觉得小红和小明同学谁的盈利多？请说明理由.

22．已知实数，函数．

（1）若函数在中有极值，求实数的取值范围；

（2）若函数有唯一的零点，求证：．

（参考数据，）

 2020-2021年度第二学期高二年级期中质量调查（数学）答题纸

二、填空题（本题共6小题，每小题5分，共30分）

13.                                 14.                                  

15.                                16.                              

17.                                18.                              

参考答案

1．C   2．D   3．C  4．B    5．B   6.D    7．A   8.D    9．A    10．D    11．B   12．A

【详解】

因为，所以，则可化为，

整理得，因为，所以，

令，则函数在上递减，

则在上恒成立，

所以在上恒成立，

令，则在上恒成立，

则在上递减，所以，

故只需满足：.

故选：A.

13．9    14．    15．    16．5        17．15    18．

19．（1）函数的解析式为；（2）在，上是增函数，在，上是减函数.

【解析】

（1），由导数的几何意义得，于是，由切点在直线上得，解得，所以函数的解析式为

（2）

当时，显然，这时在上是增函数

当时，，解得

所以在，上是增函数，在，上是减函数.

20．（1）递增区间为，递减区间为，；（2）；（3）

【详解】

（1）函数，

则导函数，

∵满足，，

∴，得，，

则，

，

令，解得，

由得，得，解得，

此时函数单调递增，即递增区间为，

由得，得，解得或，

此时函数单调递减，即递减区间为，；

综上所述，的递增区间为，的递减区间为，；

（2）由（1）知，当时，函数取得极小值，

，，

则在区间上的最大值为，

则.

（3）由（1）知当时，函数取得极小值，

当时，函数取得极大值，

若函数的图象与轴有三个交点，

则得，

得，

即的范围是.

21．（1）；（2）小明的盈利多，理由见解析.

【详解】

（1）设这个小球掉入5号球槽为事件，掉入5号球槽，需要向右4次向左2次，所以，

所以这个小球掉入5号球槽的概率为.

（2）小红的收益计算如下：每一次游戏中，的可能取值为0，4，8，12.

，

，

，

.

一次游戏付出的奖金，则小红的收益为.

小明的收益计算如下：每一次游戏中，的可能取值为0，1，4，9.

，

，

，

.

一次游戏付出的奖金，则小明的收益为.

显然，，所以小明的盈利多.

22．（1）；（2）证明见解析．

【详解】

（1），令得：，

由得：，在上单调递增，

当时，，

函数在中有极值，与在上有交点，

（2）在上单调递增，且当时，；当时，，

在有唯一零点，设零点为，则有…①，

在单调递减，在单调递增，

又函数有唯一的零点，且当时，；当时，，

，即，

将①式代入得：，

记，则为函数的零点，

，

则当时，；当时，；

在上单调递增，在上单调递减，

且当时，，，当时，，

有唯一零点，

又，，

.