2021学年最大公因数优质备课课件ppt

4　约　分

第1课时　最大公因数

备教材内容

1．本课时学习的是教材60～61页的内容及相关习题。

2．例1教学公因数和最大公因数的概念。教材直接提出：“8和12公有的因数是哪几个？公有的最大因数是多少？”并直接给予解答提示：“我先分别找出8和12的因数。”引导学生分别找出8和12的因数。在小精灵“还可以这样表示”的提示下，用集合圈直观呈现8和12各自的因数，从而引出公因数、最大公因数的概念。例2是以18和27为例，教学怎样求两个数的最大公因数。教材首先呈现了两种求最大公因数的方法。一种是根据定义，先分别写出18和27各自的因数，然后从中找出两个数的公因数、最大公因数；另一种是先写出18(两数中较小数)的因数，再从中圈出27的因数，再看哪个最大。

3．本课时的内容是在学生已经理解和掌握因数的含义，初步学会找一个数的因数，知道一个数因数的特点的基础上进行教学的。这部分内容既是“数与代数”领域基础知识的重要组成部分，又是接下来学习约分和分数四则运算的基础。对于学生后续的学习和发展，有着举足轻重的作用。

备已学知识

备教学目标

知识与技能

1．理解公因数和最大公因数的意义，知道因数、公因数和最大公因数的区别和联系。

2．掌握求两个数的最大公因数的方法，会选择合适的方法求两个数的最大公因数。

过程与方法

经历认识最大公因数和求最大公因数的过程，体验知识迁移、推理判断的学习方法。

情感、态度与价值观

在学习活动中体会数学知识之间的密切联系，激发求知欲望，培养合作意识与探索精神，养成善于观察、勤于思考的良好学习习惯。

备重点难点

重点：理解公因数和最大公因数的意义，能正确求出两个数的最大公因数。

难点：掌握求两个数的最大公因数的方法。

备知识讲解

知识点一 公因数和最大公因数的意义

问题导入　8和12公有的因数是哪几个？公有的最大因数是多少？(教材60页例1)

过程讲解　

1．读题，理解题意并确定解题方法

要找8和12公有的因数，可以先分别列出8和12各自的因数，然后找出哪些因数是8和12公有的，最后从中选出最大公因数。

2．列举出8和12的所有因数

3．解决问题

8和12公有的因数是1，2，4；8和12公有的最大因数是4。

4.明确公因数和最大公因数的意义

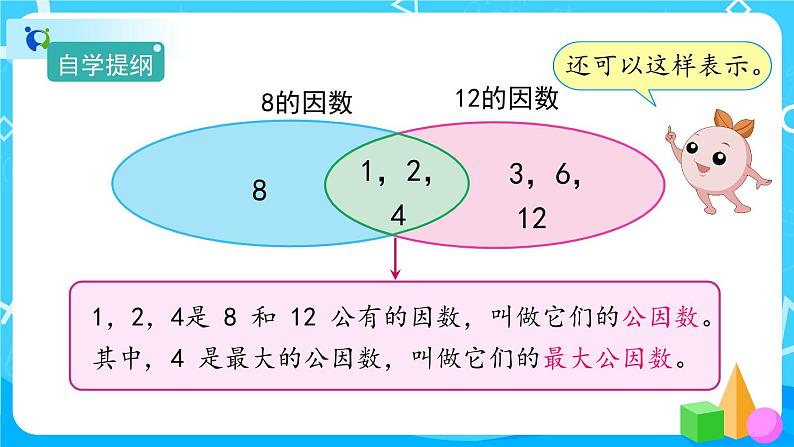
1，2，4是8和12公有的因数，叫做它们的公因数。其中，4是最大的公因数，叫做它们的最大公因数。

5．明确公因数的表示方法

方法一　列举法。

8和12的公因数有1，2，4；8和12的最大公因数是4。

方法二　集合法。

[思想方法解读：用集合法表示8和12的因数和公因数渗透了集合思想。集合思想就是运用集合的概念、逻辑语言、图形等来解决问题的思想方法。]

归纳总结

几个数公有的因数叫做这几个数的公因数。其中最大的一个叫做这几个数的最大公因数。

知识点二 求两个数最大公因数的方法

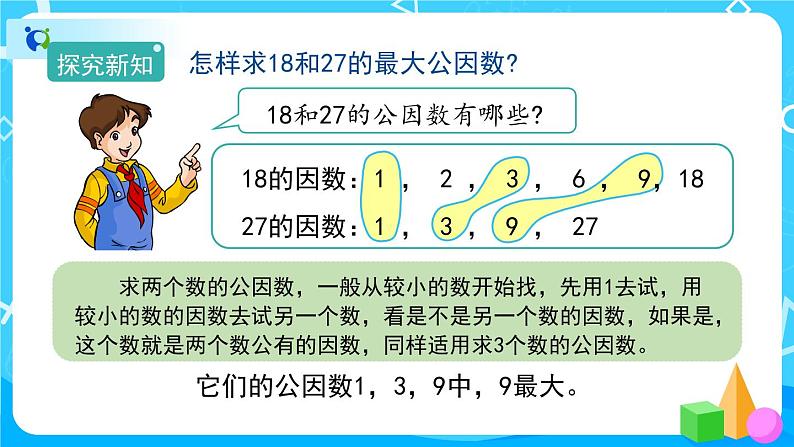
问题导入　怎样求18和27的最大公因数？(教材60页例2)

方法讲解

方法一　列举法。

(1)方法分析：先分别找出18和27各自的因数，再找出它们的公因数，最后从中找出最大的一个。

(2)解答过程。

18和27的公因数有1，3，9。

18和27的最大公因数是9。

方法二　筛选法。

(1)方法分析：先找出两个数中较小数18的因数，再看18的因数中，哪些是27的因数，并从中找出最大的一个。

(2)解答过程。

18的因数：①，2，③ ，6，⑨ ，18

在18的因数中，1，3，9是27的因数。

18和27的最大公因数是9。

(3)方法改进。

写出18的因数：1，2，3，6，9，18。从大到小依次看18的因数是不是27的因数，18不是27的因数，9是27的因数，所以9是18和27的最大公因数，这样找最大公因数更快捷。

方法三　分解质因数法。

(1)方法分析：把18和27分别分解质因数，18＝2×3×3，27＝3×3×3。18和27的公因数一定包含18和27公有的质因数。最大公因数就是公因数中最大的一个，所以它一定包含18和27公有的质因数3和3，3乘3的积就是18和27的最大公因数。

(2)解答过程：

18和27的最大公因数是3×3＝9。

方法四　短除法。

(1)方法分析：用18和27公有的最小质因数3去除这两个数，一直除到两个商只有公因数1为止，然后把所有的除数相乘，所得的积就是18和27的最大公因数。

(2)解答过程：　

18和27的最大公因数是3×3＝9。

[方法提示：用列举法和筛选法求两个数的最大公因数，一般适合较小的数，而分解质因数法和短除法适合任意的数。]

归纳总结

求两个数的最大公因数的方法：(1)列举法：先分别找出两个数的因数，从中找出公因数，再找出公因数中最大的一个。(2)筛选法：先找出两个数中较小数的因数，从中圈出较大数的因数，再看哪一个因数最大。(3)分解质因数法：先将这两个数分别分解质因数，再从分解的质因数中找出这两个数公有的质因数，公有的质因数相乘所得的积就是这两个数的最大公因数。(4)短除法：先把两个数公有的质因数按从小到大的顺序依次作为除数，连续去除这两个数，直到得出的两个商只有公因数1为止，再把所有的除数相乘，所得的积就是这两个数的最大公因数。

拓展提高

1．两个数的公因数是它们最大公因数的因数，最大公因数是公因数的倍数。如18和27的公因数有1，3和9，9是18和27的最大公因数，1和3是9的因数，9是1和3的倍数。

2．若干个连续自然数的公因数只有1，则它们的最大公因数也是1。

知识点三 求两个数最大公因数的特殊情况

问题导入　找出下列每组数的最大公因数。你发现了什么？(教材61页“做一做”3题)

4和8　　12和36　　1和7　　8和9　　12和35

过程讲解　

1．找出每组数的最大公因数

4和8的最大公       12和36的最大

因数是4。　　　　   公因数是12。

1和7的最大公　　　 　8和9的最大

因数是1。             公因数是1。

       12和35的最大公因数是1。

2．观察每组中两个数的特点

 最大公因数是较小数。

 最大公因数是1。

归纳总结

1．当两个数成倍数关系时，较小数就是它们的最大公因数。

2．当两个数的公因数只有1时，它们的最大公因数就是1。

知识点四 互质数的意义和判断方法

问题导入　找出下列每组数的公因数，你发现了什么？

5和7　　　7和9　　　　14和15

过程讲解　

1．找出每组数的公因数，并说一说你发现了什么

发现：每组数中的两个数的公因数只有1。

2．明确互质数的概念

公因数只有1的两个数叫做互质数。例如：5和7，7和9，14和15都是互质数。

3．明确互质数的判断方法

互质数有很多种情况，不是只有两个质数才是互质数，合数和合数也可能成为互质数，如15和16就是一对互质数。判断两个数是不是互质数，要看它们是不是只有公因数1。

4．互质数的特殊情况

(1)1和任意非0的自然数都是互质数。(2)2和任意奇数都是互质数。(3)相邻的两个非0自然数是互质数。(4)相邻的两个奇数是互质数。(5)不相同的两个质数是互质数。(6)一个合数与一个质数是互质数(合数是质数的倍数除外)。

5．互质数和质数的区别

质数是一类数，是只有1和它本身两个因数的数；互质数是对于两个数的关系而言的，公因数只有1的两个数是互质数。

归纳总结

公因数只有1的两个数叫做互质数。

备易错易混

误区一 判断：两个合数的最大公因数不可能是1。(√)

错解分析　此题错在忽略了两个合数是互质数的情况，如14和15，27和32，它们的最大公因数都是1。

错解改正　×

温馨提示

如果两个数是互质数，那么它们的最大公因数就是1。

误区二 判断：两个数的最大公因数一定比这两个数都小。(√)

错解分析　此题错在忽略了当两个数是倍数关系时，较小数就是它们的最大公因数。

错解改正　×

温馨提示

在求两个数的最大公因数时，若两个数存在倍数关系，则这两个数的最大公因数就是较小数。

备综合能力

方法运用 运用辗转相除法解决求两个数的最大公因数问题

典型例题　求9021和9991的最大公因数。

思路分析　9021和9991这两个数比较大，它们的公因数很难找，可以用辗转相除法求它们的最大公因数。第一步：用较大数除以较小数，即9991÷9021＝1……970；第二步：用上一步中的除数除以余数，即9021÷970＝9……291；第三步：同上一步，即970÷291＝3……97；第四步：同上一步，即291÷97＝3。直到整除为止，最后一个除数97就是9021和9991的最大公因数。

正确解答　9021和9991的最大公因数是97。

方法总结 用辗转相除法求两个数的最大公因数时，先用较大数除以较小数，除得的余数作为下一次相除的除数，上一次相除的除数作为下一次相除的被除数，除到商是整数为止，此时的除数就是这两个数的最大公因数。

方法运用 运用分类法解决数字分组问题

典型例题　将14，30，33，35，39，75，143，169这八个数平均分成两组，使这两组数的乘积相等。你知道怎样分组吗？请写出分组方法。

思路分析　根据“含有的质因数完全相同，乘积相等”解答此题，如下：

(1)分解质因数：14＝2×7　30＝2×3×5

33＝3×11　35＝5×7　39＝3×13

75＝3×5×5　143＝11×13　169＝13×13

(2)统计每个质因数的个数：2个2，2个7，4个3，4个5，4个13，2个11。

(3)因为题中要求将这八个数平均分成两组，使这两组数的乘积相等，所以每组数中要有1个2，1个7，2个3，2个5，2个13，1个11，可以得出：

第一组数：14，39，75，143

第二组数：30，33，35，169

或第一组数：14，33，75，169

第二组数：30，35，39，143

正确解答　方法一　第一组数：14，39，75，143；第二组数：30，33，35，169。

方法二　第一组数：14，33，75，169；第二组数：30，35，39，143。

方法总结 解决此类问题，需将每个数分解质因数，然后根据质因数将数分组。

备教学资料

求最大公因数的方法

求几个数的最大公因数，开始用观察比较的方法，即先把每个数的因数找出来，再找出公因数，最后在公因数中找出最大公因数。后来用分解质因数的方法求两个数的因数，再进行计算。之后又演变为短除法，用质因数去除两个数，最后进行整理。短除法也可以用来求最小公倍数。

短除符号就是把除号倒过来。其方法是在除法中写除数的地方写两个数公有的质因数，然后落下两个数被公有的质因数整除的商，之后再除，以此类推，直到结果是互质数为止。