必修 第一册3 函数的单调性和最值背景图ppt课件

这是一份必修 第一册3 函数的单调性和最值背景图ppt课件，共52页。

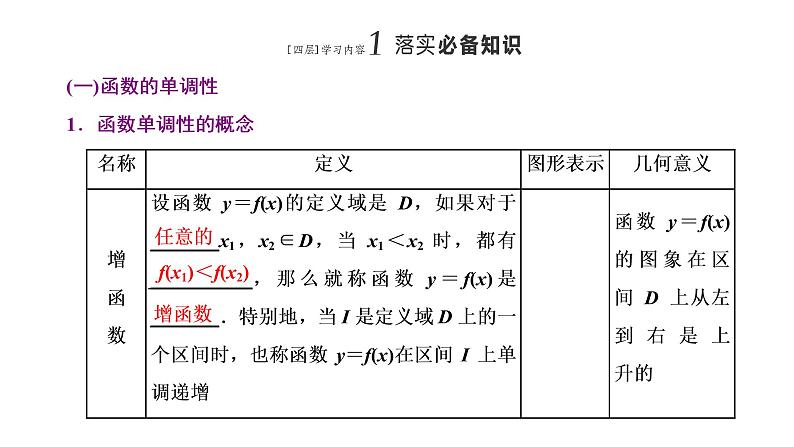
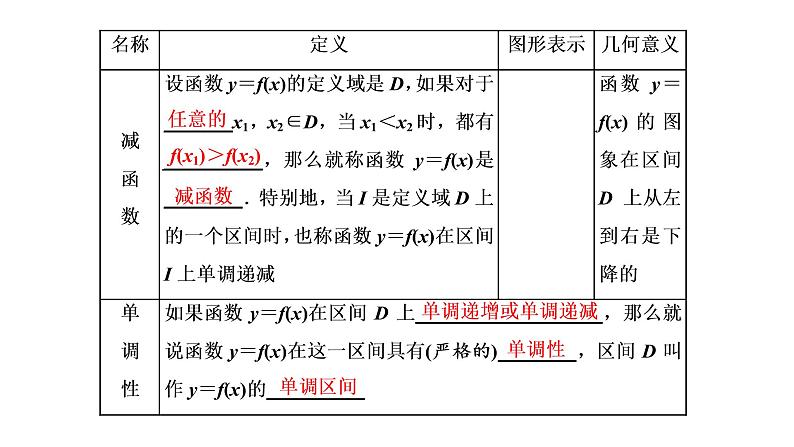
1．对增函数与减函数定义的理解(1)定义中x1，x2有三个特征：一是x1，x2同属于一个单调区间；二是x1，x2是任意的两个实数，证明单调性时不可随意用两个特殊值代替；三是x1与x2有大小，通常规定x1＜x2，但也可规定x2＜x1.(2)函数的递增(或递减)是针对定义域I内的某个区间D而言的，显然D⊆I.(3)当函数值的改变量与其对应的自变量的改变量符号相同时，函数单调递增；符号相反时，函数单调递减．
2．对函数单调区间的理解(1)函数的单调区间是其定义域内的某一个区间，如函数y＝x2＋2x－1的单调减区间(－∞，－1]⊆(－∞，＋∞)，故在讨论函数的单调性时，必须先确定函数的定义域．(2)若函数y＝f(x)在其定义域内的两个区间A，B上都是单调递增(递减)的，一般不认为y＝f(x)在区间A∪B上一定是单调递增(递减)的．如：函数f(x)＝在区间(－∞，0)上是单调递减的，在区间(0，＋∞)上也是单调递减的，但不能说它在整个定义域(－∞，0)∪(0，＋∞)上是单调递减的．(3)对于单独的一点，由于它的函数值是唯一确定的常数，没有增减变化，所以不存在单调性，因此在写单调区间时，可以包括端点，也可以不包括端点．———————————————————————————————————
[即时小练]1．判断正误(1)因为f(－1)f(1)． (　　)(3)若函数f(x)在区间(1,2]和(2,3)上均单调递增，则函数f(x)在区间(1,3)上单调递增． (　　)(4)若函数y＝f(x)在区间D上单调递增，则函数y＝－f(x)在区间D上单调递减． (　　)答案：(1)×　(2)√　(3)×　(4)√
2．(多选)下列函数在区间(0，＋∞)上单调递增的是 (　　)A．y＝2x＋1　　　　　　B．y＝x2＋1C．y＝3－x D．y＝x2＋2x＋1答案：ABD
函数的最值和值域的区别和联系联系：函数的最值和值域反映的都是函数的整体性质，针对的是整个定义域．区别：(1)函数的值域一定存在，而函数的最大(小)值不一定存在；(2)若函数的最值存在，则最值一定是值域中的元素．例如，函数f(x)＝x2对任意的x∈R，都有f(x)≥－1，但是f(x)的最小值不是－1，因为－1不在f(x)的值域内；(3)若函数的值域是开区间(两端点都取不到)，则函数无最值；若函数的值域是闭区间，则闭区间的端点值就是函数的最值．————————————————————————————————
[方法技巧]1．求单调区间的注意点由函数的图象得出单调区间是常用的一种方法，但一定要注意画图的准确性及端点处的处理．若函数的定义域内不含区间端点，则要写成开区间；若区间端点在其定义域内，则写成开区间或闭区间均可，但最好加上区间端点．
(2)由(1)可知，当x∈[－4，－1]和[1,2]时函数单调递增，x∈[－1,1]时函数单调递减，∴f(x)max＝f(－1)＝1，f(x)min＝f(－4)＝－8，∴f(x)的最大值为1，最小值为－8.
2．作差变形的常用技巧(1)因式分解．当原函数是多项式函数时，作差后的变形通常进行因式分解．如f(x)＝x2－2x－3＝(x－3)(x＋1)．(2)通分．当原函数是分式函数时，作差后往往进行通分，然后对分子进行因式分解．(3)配方．当所得的差式是含有x1，x2的二次三项式时，可以考虑配方，便于判断符号．(4)分子有理化．当原函数是根式函数时，作差后往往考虑分子有理化．　　
[拓展]1．在本例(1)中，若函数f(x)＝－x2－2(a＋1)x＋3的单调递增区间是(－∞，3]，则实数a的值为________．解析：f(x)＝－x2－2(a＋1)x＋3＝－(x＋a＋1)2＋(a＋1)2＋3.因此函数的单调递增区间为(－∞，－a－1]，由题意得－a－1＝3，a＝－4.答案：－4
(2)解不等式当函数f(x)的解析式未知时，欲求解不等式，可以依据函数单调性的定义和性质，将符号“f”去掉，列出关于自变量的不等式(组)，然后求解，此时注意函数的定义域．(3)比较大小利用函数的单调性可以比较函数值或自变量的大小，在解决比较函数值大小的问题时，需要自变量在同一个单调区间上，然后利用单调性比较大小．　　
2．已知函数y＝f(x)在R上单调递增，且f(m2＋1)＜f(－m＋1)，则实数m的取值范围是 (　　)A．(－1,0) B．(－2,1)C．(0,1) D．(－∞，－1)∪(0，＋∞)解析：因为函数y＝f(x)在R上单调递增，且f(m2＋1)＜f(－m＋1)，所以m2＋1＜－m＋1，解得－1＜m＜0，故选A.答案： A　
一、在典题训练中内化学科素养函数单调性是函数的重要性质之一，高考一般不单独考查，常与最值或其他内容综合考查，在此过程中体现数学运算与逻辑推理的核心素养．
强化拓广探索3．是否存在函数f(x)，其在定义域上既不是增函数，也不是减函数？如果不存在，说明理由；如果存在，举出实例．提示：存在，如：f(x)＝c(c为常数)，f(x)＝x2在定义域R上既不是增函数，也不是减函数．(答案不唯一)
4．如果函数y＝f(x)(x∈D，D为此函数的定义域)同时满足下列两个条件：①函数f(x)在D上单调递增或单调递减；②存在区间[a，b]⊆D，使函数f(x)在区间[a，b]上的取值范围为[a，b]．那么称y＝f(x)，x∈D为闭函数．请回答以下问题：(1)判断函数f(x)＝1＋x－x2(x>0)是否为闭函数，并说明理由；(2)若y＝k＋(k＜0)是闭函数，求实数k的取值范围．
““四翼”检测评价”见““四翼”检测评价(十七)” (单击进入电子文档)