人教版高中数学高考一轮复习训练--　空间直线、平面的平行

这是一份人教版高中数学高考一轮复习训练--　空间直线、平面的平行，共8页。试卷主要包含了基础巩固，综合应用，探究创新等内容，欢迎下载使用。

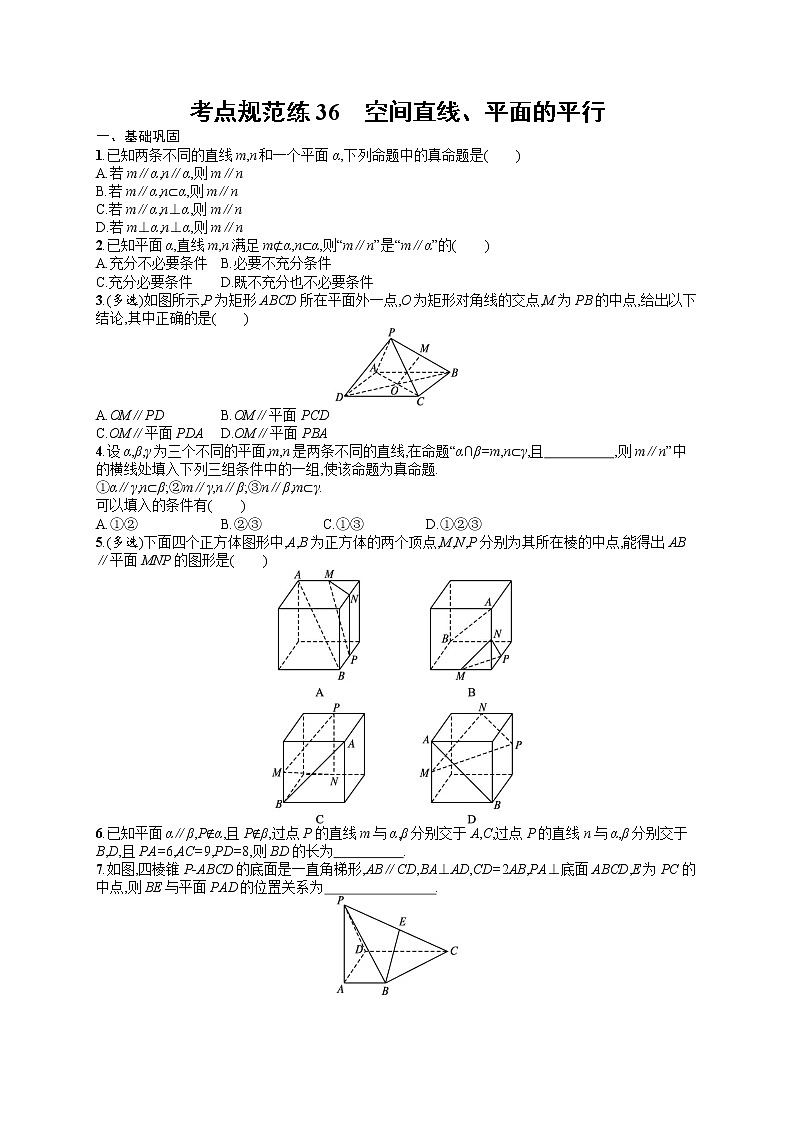
1.已知两条不同的直线m,n和一个平面α,下列命题中的真命题是( )
A.若m∥α,n∥α,则m∥n
B.若m∥α,n⊂α,则m∥n
C.若m∥α,n⊥α,则m∥n
D.若m⊥α,n⊥α,则m∥n
2.已知平面α,直线m,n满足m⊄α,n⊂α,则“m∥n”是“m∥α”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
3.(多选)如图所示,P为矩形ABCD所在平面外一点,O为矩形对角线的交点,M为PB的中点,给出以下结论,其中正确的是( )
A.OM∥PDB.OM∥平面PCD
C.OM∥平面PDAD.OM∥平面PBA
4.设α,β,γ为三个不同的平面,m,n是两条不同的直线,在命题“α∩β=m,n⊂γ,且 ,则m∥n”中的横线处填入下列三组条件中的一组,使该命题为真命题.
①α∥γ,n⊂β;②m∥γ,n∥β;③n∥β,m⊂γ.
可以填入的条件有( )
A.①②B.②③C.①③D.①②③
5.(多选)下面四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是( )
6.已知平面α∥β,P∉α,且P∉β,过点P的直线m与α,β分别交于A,C,过点P的直线n与α,β分别交于B,D,且PA=6,AC=9,PD=8,则BD的长为 .
7.如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为 .
8.在正四棱柱ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,则点Q满足条件 时,有平面D1BQ∥平面PAO.
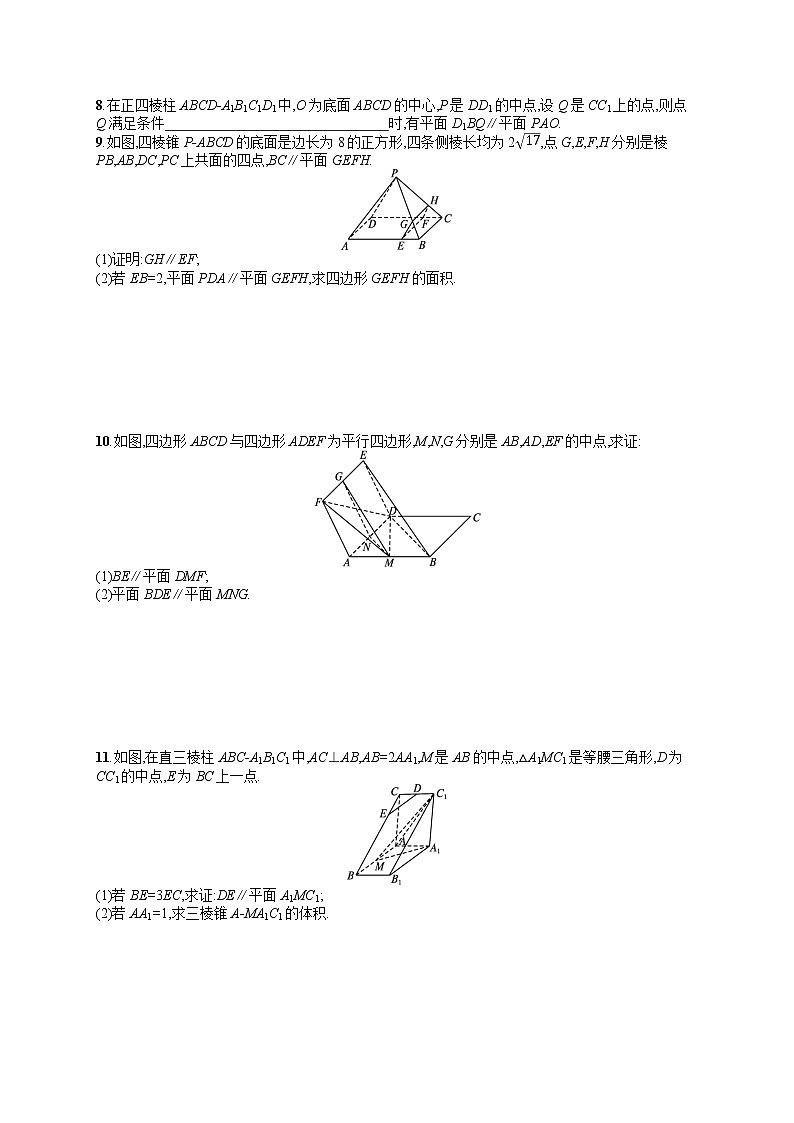
9.如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为217,点G,E,F,H分别是棱PB,AB,DC,PC上共面的四点,BC∥平面GEFH.
(1)证明:GH∥EF;
(2)若EB=2,平面PDA∥平面GEFH,求四边形GEFH的面积.
10.如图,四边形ABCD与四边形ADEF为平行四边形,M,N,G分别是AB,AD,EF的中点,求证:
(1)BE∥平面DMF;
(2)平面BDE∥平面MNG.
11.如图,在直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
(1)若BE=3EC,求证:DE∥平面A1MC1;
(2)若AA1=1,求三棱锥A-MA1C1的体积.
二、综合应用
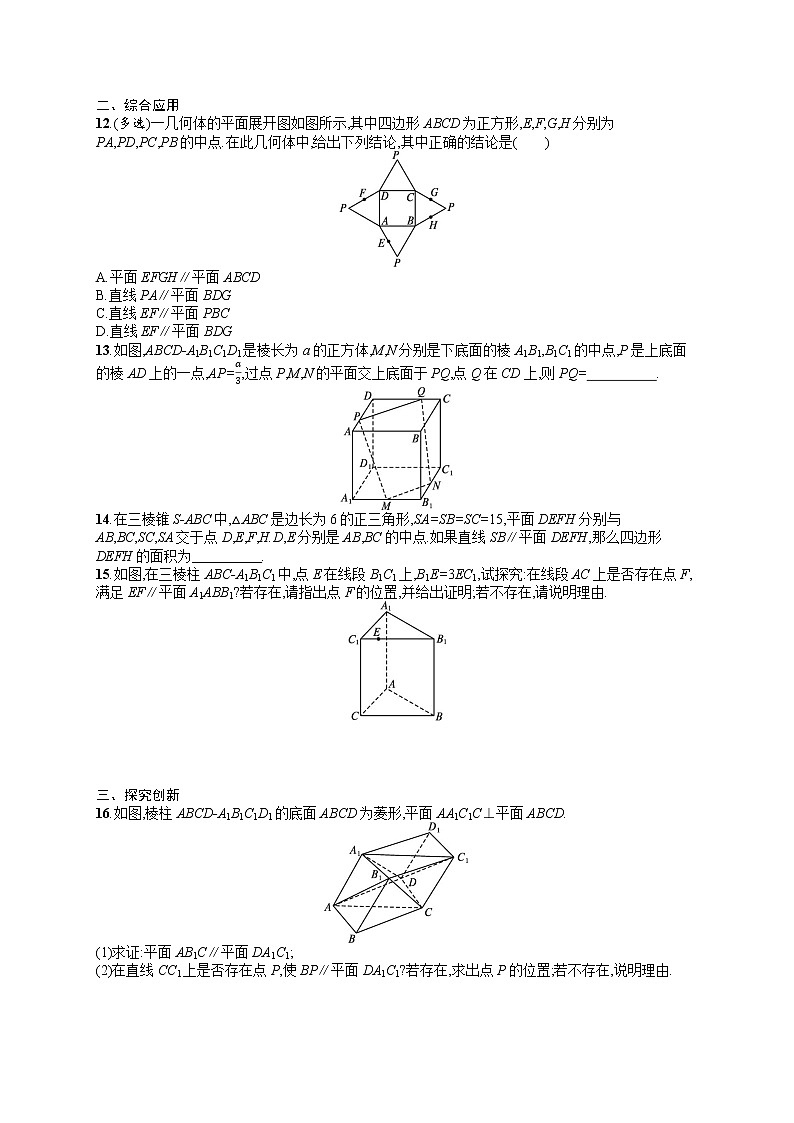
12.(多选)一几何体的平面展开图如图所示,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点.在此几何体中,给出下列结论,其中正确的结论是( )
A.平面EFGH∥平面ABCD
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
13.如图,ABCD-A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=a3,过点P,M,N的平面交上底面于PQ,点Q在CD上,则PQ= .
14.在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB,BC,SC,SA交于点D,E,F,H.D,E分别是AB,BC的中点.如果直线SB∥平面DEFH,那么四边形DEFH的面积为 .
15.如图,在三棱柱ABC-A1B1C1中,点E在线段B1C1上,B1E=3EC1,试探究:在线段AC上是否存在点F,满足EF∥平面A1ABB1?若存在,请指出点F的位置,并给出证明;若不存在,请说明理由.
三、探究创新
16.如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.
(1)求证:平面AB1C∥平面DA1C1;
(2)在直线CC1上是否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
考点规范练36 空间直线、平面的平行
1.D 对于A,直线m,n可能平行、异面或相交,故A错误;对于B,直线m与n可能平行,也可能异面,故B错误;对于C,m与n垂直而非平行,故C错误;对于D,垂直于同一平面的两直线平行,故D正确.
2.A 当m⊄α,n⊂α时,由线面平行的判定定理可知,m∥n⇒m∥α;反之m∥α不一定有m∥n,m与n还可能异面.故选A.
3.ABC 由题意知,OM是△BPD的中位线,所以OM∥PD,故A正确;
因为PD⊂平面PCD,OM⊄平面PCD,所以OM∥平面PCD,故B正确;
同理,可得OM∥平面PDA,故C正确;
OM与平面PBA相交,故D不正确.
4.C 由面面平行的性质定理可知,①正确;当n∥β,m⊂γ时,n和m在同一平面内,且没有公共点,所以平行,③正确.故选C.
5.AD A中,如图①,连接BC,由已知得AC∥NP,BC∥MN,从而得AC∥平面MNP,BC∥平面MNP,于是有平面ABC∥平面MNP,所以AB∥平面MNP.
B中,如图②,连接BC,交MP于点O,连接ON,易知在底面正方形中O不是BC中点(实际上是靠近C的四等分点),而N是AC中点,因此AB与ON不平行,在平面ABC内,AB与ON必相交,此交点也是直线AB与平面MNP的公共点,直线AB与平面MNP相交而不平行.
C中,如图③,连接BN,正方体中有PN∥BM,因此点B在平面MNP内,直线AB与平面MNP相交而不平行.
D中,如图④,连接CD,可得AB∥CD,CD∥NP,即AB∥NP,从而直线AB与平面MNP平行.
6.245或24 如图(1),∵AC∩BD=P,
图(1)
∴经过直线AC与BD可确定平面PCD.
∵α∥β,α∩平面PAB=AB,β∩平面PCD=CD,
∴AB∥CD.∴PAAC=PBBD,
即69=8-BDBD.
解得BD=245.
如图(2),同理可证AB∥CD.
图(2)
∴PAPC=PBPD,即63=BD-88.
解得BD=24.
综上所述,BD=245或24.
7.平行 取PD的中点F,连接EF,AF,在△PCD中,EF12CD.
∵AB∥CD,且CD=2AB,
∴EFAB,
∴四边形ABEF是平行四边形,
∴BE∥AF.
又BE⊄平面PAD,AF⊂平面PAD,
∴BE∥平面PAD.
8.Q为CC1的中点 如图,设Q为CC1的中点,因为P为DD1的中点,
所以QB∥PA.
连接DB,因为P,O分别是DD1,DB的中点,所以D1B∥PO.
又D1B⊄平面PAO,QB⊄平面PAO,
所以D1B∥平面PAO,QB∥平面PAO.
又D1B∩QB=B,所以平面D1BQ∥平面PAO.
故当Q满足条件Q为CC1的中点时,有平面D1BQ∥平面PAO.
9.(1)证明 ∵BC∥平面GEFH,
又BC⊂平面PBC,且平面PBC∩平面GEFH=GH,
∴BC∥GH.
又BC∥平面GEFH,BC⊂平面ABCD,
且平面ABCD∩平面GEFH=EF,
∴BC∥EF,∴EF∥GH.
(2)解 ∵平面PDA∥平面GEFH,平面PAB∩平面PAD=PA,平面PAB∩平面GEFH=GE,
∴GE∥PA.
∵BE=14AB,∴GE=14PA=172,
同理HF=14PD=172,
又由(1)知,BC∥GH,∴GH=34BC=6.
在四边形GEFH中,GE=HF=172,GH=6,EF=8,且EF∥GH,
四边形GEFH为等腰梯形,
如图,过点G作GM垂直于EF于点M,过点H作HN垂直于EF于点N,
在Rt△GEM中,GM=GE2-EM2=132,
∴S梯形GEFH=12(GH+EF)·GM=7132.
10.证明 (1)如图,连接AE,设DF与GN的交点为O,
则AE必过DF与GN的交点O.
连接MO,则MO为△ABE的中位线,所以BE∥MO.
又BE⊄平面DMF,MO⊂平面DMF,
所以BE∥平面DMF.
(2)因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以DE∥GN.
又DE⊄平面MNG,GN⊂平面MNG,所以DE∥平面MNG.
又M为AB的中点,所以MN为△ABD的中位线,
所以BD∥MN.又BD⊄平面MNG,MN⊂平面MNG,所以BD∥平面MNG.
又DE⊂平面BDE,BD⊂平面BDE,DE∩BD=D,
所以平面BDE∥平面MNG.
11.(1)证明 如图①,取BC的中点N,连接MN,C1N,
①
∵M是AB的中点,∴MN∥AC∥A1C1,
∴M,N,C1,A1共面.
∵BE=3EC,∴E是NC的中点.
又D是CC1的中点,∴DE∥NC1.
∵DE⊄平面MNC1A1,NC1⊂平面MNC1A1,
∴DE∥平面A1MC1.
(2)解 如图②,当AA1=1时,有AM=1,A1M=2,A1C1=2.
∴三棱锥A-MA1C1的体积VA-MA1C1=VC1-A1AM=13×12AM·AA1·A1C1=26.
②
12.ABC 作出立体图形,如图所示.连接E,F,G,H四点构成平面EFGH.
对于A,因为E,F分别是PA,PD的中点,所以EF∥AD.
又EF⊄平面ABCD,AD⊂平面ABCD,所以EF∥平面ABCD.同理,EH∥平面ABCD.又EF∩EH=E,EF⊂平面EFGH,EH⊂平面EFGH,
所以平面EFGH∥平面ABCD,故A正确;对于B,连接AC,BD,DG,BG,设AC的中点为M,则M也是BD的中点,所以MG∥PA,又MG⊂平面BDG,PA⊄平面BDG,所以PA∥平面BDG,故B正确;对于C,由A中的分析知EF∥AD,AD∥BC,所以EF∥BC,因为EF⊄平面PBC,BC⊂平面PBC,所以直线EF∥平面PBC,故C正确;对于D,根据C中的分析可知EF∥BC,再结合图形可得BC∩BD=B,则直线EF与平面BDG不平行,故D错误.
13.22a3 如图所示,连接AC.
∵平面PQNM交正方体的上、下底面分别于PQ,MN,
∴MN∥PQ.又MN∥AC,
∴PQ∥AC.
∵AP=a3,∴PDAD=DQCD=PQAC=23,∴PQ=23AC=22a3.
14.452 取AC的中点G,连接SG,BG.易知SG⊥AC,BG⊥AC,故AC⊥平面SGB,所以AC⊥SB.因为SB∥平面DEFH,SB⊂平面SAB,平面SAB∩平面DEFH=HD,所以SB∥HD.同理SB∥FE.又D,E分别为AB,BC的中点,所以H,F分别为AS,SC的中点,从而得HF12ACDE,所以四边形DEFH为平行四边形.又AC⊥SB,SB∥HD,DE∥AC,所以DE⊥HD,所以四边形DEFH为矩形,其面积S=HF·HD=12AC·12SB=452.
15.解法一 当AF=3FC时,FE∥平面A1ABB1.
证明如下:如图,在平面A1B1C1内过点E作EG∥A1C1交A1B1于点G,连接AG.
因为B1E=3EC1,所以EG=34A1C1.
又因为AF∥A1C1,且AF=34A1C1,
所以AFEG,所以四边形AFEG为平行四边形,所以EF∥AG.又因为EF⊄平面A1ABB1,AG⊂平面A1ABB1,所以EF∥平面A1ABB1.
解法二 当AF=3FC时,EF∥平面A1ABB1.
证明如下:如图,在平面BCC1B1内过点E作EG∥BB1交BC于点G,
因为EG∥BB1,EG⊄平面A1ABB1,BB1⊂平面A1ABB1,
所以EG∥平面A1ABB1.
因为B1E=3EC1,所以BG=3GC,
所以FG∥AB.
又因为AB⊂平面A1ABB1,FG⊄平面A1ABB1,所以FG∥平面A1ABB1.
又因为EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,
所以平面EFG∥平面A1ABB1.
因为EF⊂平面EFG,所以EF∥平面A1ABB1.
16.(1)证明 由棱柱ABCD-A1B1C1D1的底面ABCD为菱形,可得AB1∥DC1,A1D∥B1C.
∵AB1∩B1C=B1,A1D∩DC1=D,
∴平面AB1C∥平面DA1C1.
(2)解 存在满足题意的点P.
如图,在C1C的延长线上取点P,使C1C=CP,连接BP,
∵B1BCC1,∴BB1CP,∴四边形BB1CP为平行四边形,∴BP∥B1C.
∵A1D∥B1C,
∴BP∥A1D.
又A1D⊂平面DA1C1,BP⊄平面DA1C1,
∴BP∥平面DA1C1.