数学九年级下册26.1.1 反比例函数测试题

这是一份数学九年级下册26.1.1 反比例函数测试题，共10页。试卷主要包含了5 等内容，欢迎下载使用。
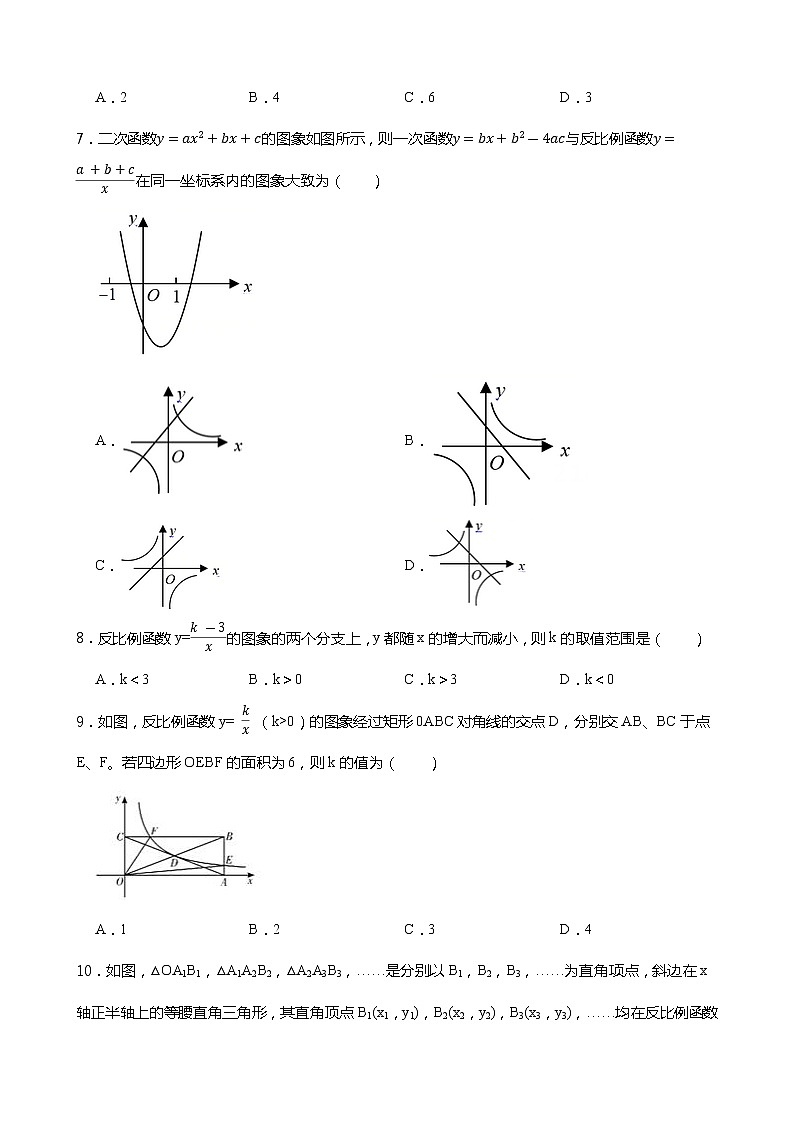
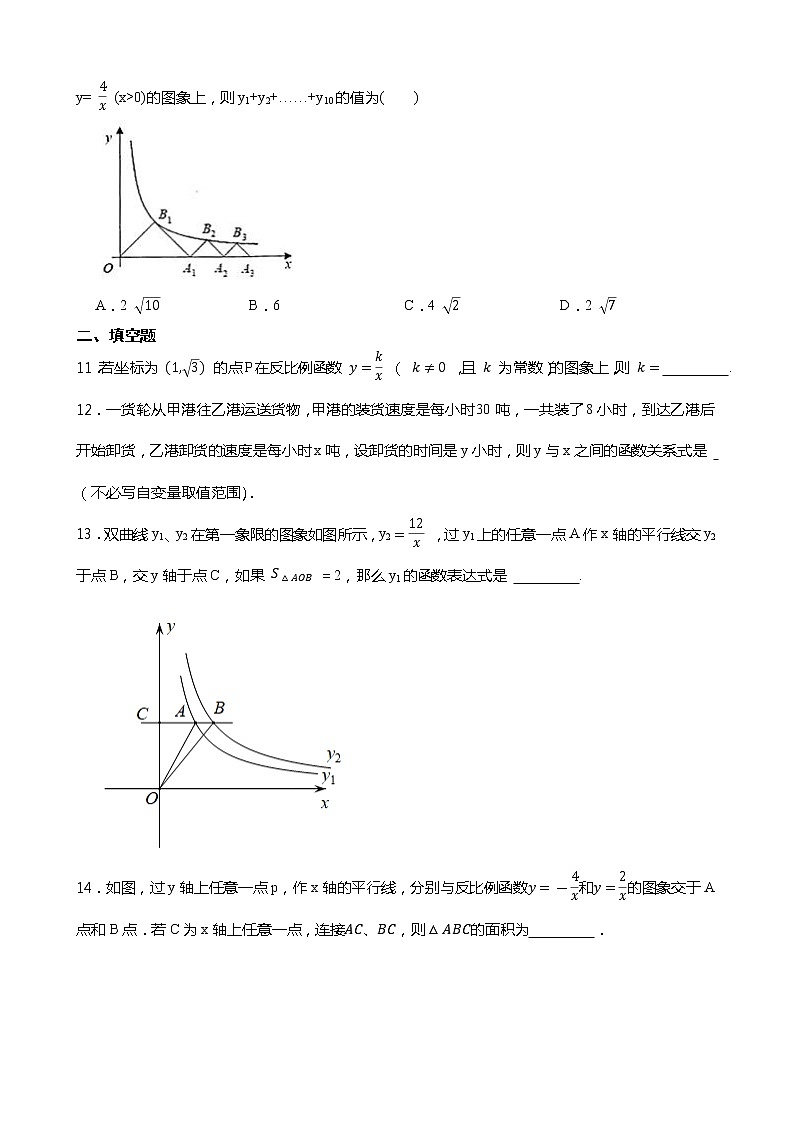
 26.1 反比例函数----人教版九年级下册同步练习一、单选题1．在下列函数中表示y关于x 的反比例函数的是（　　）  A．y=2x B． C． D．2．下列各问题中，两个变量之间的关系不是反比例函数的是         A．小明完成100m赛跑时，时间t（s）与跑步的平均速度v（m/s）之间的关系.B．菱形的面积为48cm2，它的两条对角线的长为y（cm）与x（cm）的关系.C．一个玻璃容器的体积为30L时，所盛液体的质量m与所盛液体的体积V之间的关系.D．压力为600N时，压强p与受力面积S之间的关系.3．函数 的图象经过点（－1，－2），则k的值为（　　）  A． B．－  C．2 D．－24．对于反比例函数y=（k＜0），下列说法正确的是（　　）．A．图象经过点（1，﹣k） B．图象位于第一、三象限C．图象是中心对称图形 D．当x＜0时，y随x的增大而减小5．已知：点，，都在反比例函数图象上（），则、、的关系是（　　）A． B． C． D．6．如图，Rt△AOC的直角边OC在x轴上，∠ACO=90°，反比例函数y=经过另一条直角边AC的中点D，S△AOC=3，则k=（　　）A．2 B．4 C．6 D．37．二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（　　）A． B．C． D．8．反比例函数y=的图象的两个分支上，y都随x的增大而减小，则k的取值范围是（　　）A．k＜3 B．k＞0 C．k＞3 D．k＜09．如图，反比例函数y= （k>0）的图象经过矩形0ABC对角线的交点D，分别交AB、BC于点E、F。若四边形OEBF的面积为6，则k的值为（　　）A．1 B．2 C．3 D．410．如图，△OA1B1，△A1A2B2，△A2A3B3，……是分别以B1，B2，B3，……为直角项点，斜边在x轴正半轴上的等腰直角三角形，其直角顶点B1(x1，y1)，B2(x2，y2)，B3(x3，y3)，……均在反比例函数y= (x>0)的图象上，则y1+y2+……+y10的值为(　　)  A．2  B．6 C．4  D．2 二、填空题11．若坐标为 的点P在反比例函数 （ ，且 为常数）的图象上，则 　     　.  12．一货轮从甲港往乙港运送货物，甲港的装货速度是每小时30吨，一共装了8小时，到达乙港后开始卸货，乙港卸货的速度是每小时x吨，设卸货的时间是y小时，则y与x之间的函数关系式是 　     　（不必写自变量取值范围）．13．双曲线y1、y2在第一象限的图象如图所示，y2 ，过y1上的任意一点A作x轴的平行线交y2于点B，交y轴于点C，如果 ＝2，那么y1的函数表达式是 　     　.14．如图，过y轴上任意一点p，作x轴的平行线，分别与反比例函数和的图象交于A点和B点．若C为x轴上任意一点，连接，则的面积为　     　．15．如图，已知菱形ABCD的对角线AC的中点与坐标原点重合，AF⊥AC交x轴于点F，反比例函数 的图象经过点A，与AF交于点E，且AE=EF，△ADF的面积为6，则k的值为　     　．三、作图题16．在函数的学习中，我们经历了“确定函数表达式——画函数图像——利用函数图像研究函数性质——利用图像解决问题”的学习过程.我们可以借鉴这种方法探究函数 的图像性质.  （1）补充表格，并画出函数的图像①列表：x…-3-10235…y…-1-2-44     　1…②描点并连线，画图.（2）观察图像，写出该函数图像的一个增减性特征：　                           　； （3）函数 的图像是由函数 的图像如何平移得到的？　                                                      　，其对称中心的坐标为　         　；   （4）根据上述经验，猜一猜函数 的图像大致位置，结合图像直接写出y≥3时，x的取值范围　     　.   四、解答题17．公司员工甲去距离单位6千米的社区医院接种新冠疫苗，去时骑自行车，在医院等候和接种疫苗花了2小时，回来时发现时间可能来不及了，改乘汽车返回公司，已知其骑自行车的速度不超过 ，汽车的速度是骑自行速度的1.5倍，并且公司规定在离开之时算起2.5小时内需返回公司.问甲能否规定时间内及时返回公司？    18．如图，一次函数y＝k1x+b与反比例函数y＝ 的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S△ABC＝5．  （1）求一次函数与反比例函数的解析式；（2）根据所给条件，请直接写出不等式k1x+b＞ 的解集；  （3）若P（p，y1），Q（﹣2，y2）是函数y＝ 图象上的两点，且y1≥y2，求实数p的取值范围． 
答案 1．B2．C3．C4．C5．C6．D7．D8．C9．B10．A11．12．13．14．315．-416．（1）解：补充表格，并画出函数的图像  ①列表：x…-3-10235…y…-1-2-4421…②描点并连线，画图.（2）当x＞1时，y随着x的增大减小（3）函数y= 的图象是由函数y= 的图象向右平移1个单位；（1，0）（4）1<x≤517．解：设员工甲骑自行车的速度为 ，则汽车的速度为 ，假如员工刚好在出发后2.5小时回到公司，则  解得 检验：当 ， ，∴ 是方程的解.又∵ 答：甲不能在规定时间内及时返回公司.解法二：设员工甲骑自行车的速度为 ，则汽车的速度为 ，则员工甲路上来回所花的时间 ∵ ∴当 时， 随 的增大而减小∵ .∴ ∴员工甲来回路上加等候打针时间 .∴甲不能在规定时间内及时返回公司.18．（1）把 ， 代入 得： ，  即 ，则 ，过 作 轴于 ，过 作 轴于 ，延长 、 交于 ， ， ， ， ， ， ，解得： ，即 ， ，把 代入 得： ，即反比例函数的解析式是 ；把 ， 代入 得： ，解得： ， ，即一次函数的解析式是 ；（2） ， ，  不等式 的解集是 或 ；（3）分为两种情况：当点 在第三象限时，要使 ，实数 的取值范围是 ，  当点 在第一象限时，要使 ，实数 的取值范围是 ，即 的取值范围是 或 ．