初中沪科版第24章 圆综合与测试课堂检测

这是一份初中沪科版第24章 圆综合与测试课堂检测，共28页。
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，四边形ABCD内接于⊙O，若∠ADC=130°，则∠AOC的度数为（ ）
A．25°B．80°C．130°D．100°
2、下列汽车标志中既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
3、下列四个图案中，是中心对称图形但不是轴对称图形的是（ ）
A．B．C．D．
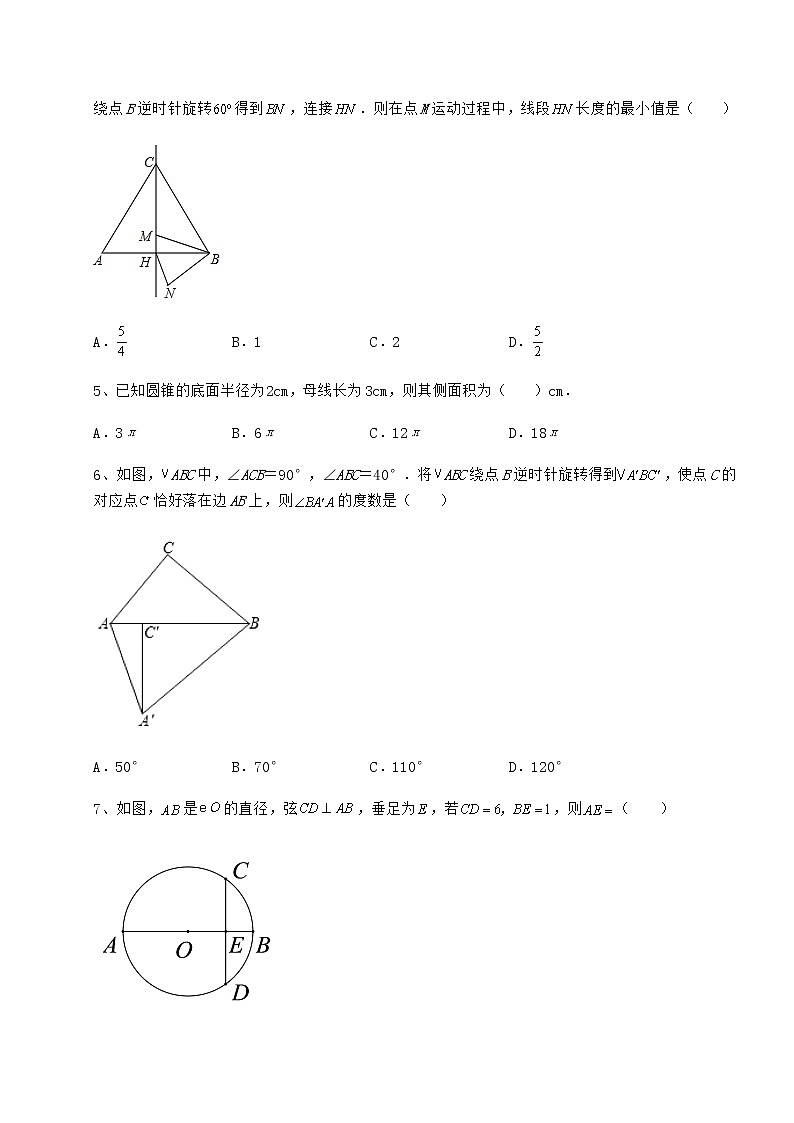
4、如图，边长为5的等边三角形中，M是高所在直线上的一个动点，连接，将线段绕点B逆时针旋转得到，连接．则在点M运动过程中，线段长度的最小值是（ ）
A．B．1C．2D．
5、已知圆锥的底面半径为2cm，母线长为3cm，则其侧面积为（ ）cm．
A．3πB．6πC．12πD．18π
6、如图，ABC中，∠ACB＝90°，∠ABC＝40°．将ABC绕点B逆时针旋转得到，使点C的对应点恰好落在边AB上，则的度数是（ ）
A．50°B．70°C．110°D．120°
7、如图，是的直径，弦，垂足为，若，则（ ）
A．5B．8C．9D．10
8、如图，点P是等边三角形ABC内一点，且PA＝3，PB＝4，PC＝5，则∠APB的度数是（ ）．
A．90°B．100°C．120°D．150°
9、如图，是△ABC的外接圆，已知，则的大小为（ ）
A．55°B．60°C．65°D．75°
10、平面直角坐标系中点关于原点对称的点的坐标是（ ）
A．B．C．D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，将半径为的圆形纸片沿一条弦折叠，折叠后弧的中点与圆心重叠，则弦的长度为________．
2、如图，一次函数的图象与x轴交于点A，与y轴交于点B，作的外接圆，则图中阴影部分的面积为______．（结果保留π）
3、已知O、I分别是△ABC的外心和内心，∠BIC＝125°，则∠BOC的大小是 ___度．
4、平面直角坐标系中，，，A为x轴上一动点，连接AC，将AC绕A点顺时针旋转90°得到AB，当BK取最小值时，点B的坐标为_________．
5、半径为6cm的扇形的圆心角所对的弧长为cm，这个圆心角______度．
三、解答题（5小题，每小题10分，共计50分）
1、如图，点A是外一点，过点A作出的一条切线．（使用尺规作图，作出一条即可，不要求写出作法，不要求证明，但要保留作图痕迹）
2、已知：如图，A为上的一点．
求作：过点A且与相切的一条直线．
作法：①连接OA；
②以点A为圆心，OA长为半径画弧，与的一个交点为B，作射线OB；
③以点B为圆心，OA长为半径画弧，交射线OB于点P（不与点O重合）；
④作直线PA．
直线PA即为所求．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：连接BA．
由作法可知．
∴点A在以OP为直径的圆上．
∴（ ）（填推理的依据）．
∵OA是的半径，
∴直线PA与相切（ ）（填推理的依据）．
3、如图，是的直径，四边形内接于，是的中点，交的延长线于点．
（1）求证：是的切线；
（2）若，，求的长．
4、已知，P是直线AB上一动点（不与A，B重合），以P为直角顶点作等腰直角三角形PBD，点E是直线AD与△PBD的外接圆除点D以外的另一个交点，直线BE与直线PD相交于点F．
（1）如图，当点P在线段AB上运动时，若∠DBE＝30°，PB＝2，求DE的长；
（2）当点P在射线AB上运动时，试探求线段AB，PB，PF之间的数量关系，并给出证明．
5、如图，已知等边内接于⊙O，D为的中点，连接DB，DC，过点C作AB的平行线，交BD的延长线于点E．
（1）求证：CE是⊙O的切线；
（2）若AB的长为6，求CE的长．
-参考答案-
一、单选题
1、D
【分析】
根据圆内接四边形的性质求出∠B的度数，根据圆周角定理计算即可．
【详解】
解：∵四边形ABCD内接于⊙O，
∴∠B+∠ADC=180°，
∵∠ADC=130°，
∴∠B=50°，
由圆周角定理得，∠AOC=2∠B=100°，
故选：D．
【点睛】
本题考查的是圆内接四边形的性质和圆周角定理，掌握圆内接四边形的对角互补是解题的关键．
2、C
【分析】
根据轴对称图形与中心对称图形的概念求解．
【详解】
解：A、是轴对称图形，不是中心对称图形，故此选项不符合题意；
B、是轴对称图形，不是中心对称图形，故此选项不符合题意；
C、是轴对称图形，是中心对称图形，故此选项符合题意；
D、不是轴对称图形，是中心对称图形，故此选项不符合题意；
故选：C．
【点睛】
此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
3、D
【分析】
根据轴对称图形与中心对称图形的概念求解．
【详解】
解：A、不是轴对称图形，不是中心对称图形，故此选项不符合题意；
B、是轴对称图形，不是中心对称图形，故此选项不符合题意；
C、是轴对称图形，是中心对称图形，故此选项不符合题意；
D、不是轴对称图形，是中心对称图形，故此选项符合题意；
故选：D．
【点睛】
此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
4、A
【分析】
取CB的中点G，连接MG，根据等边三角形的性质可得BH=BG，再求出∠HBN=∠MBG，根据旋转的性质可得MB=NB，然后利用“边角边”证明△MBG≌△NBH，再根据全等三角形对应边相等可得HN=MG，然后根据垂线段最短可得MG⊥CH时最短，再根据∠BCH=30°求解即可．
【详解】
解：如图，取BC的中点G，连接MG，
∵旋转角为60°，
∴∠MBH+∠HBN=60°，
又∵∠MBH+∠MBC=∠ABC=60°，
∴∠HBN=∠GBM，
∵CH是等边△ABC的对称轴，
∴HB=AB，
∴HB=BG，
又∵MB旋转到BN，
∴BM=BN，
在△MBG和△NBH中，
，
∴△MBG≌△NBH（SAS），
∴MG=NH，
根据垂线段最短，MG⊥CH时，MG最短，即HN最短，
此时∵∠BCH=×60°=30°，CG=AB=×5=2.5，
∴MG=CG=，
∴HN=，
故选A．
【点睛】
本题考查了旋转的性质，等边三角形的性质，全等三角形的判定与性质，垂线段最短的性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．
5、B
【分析】
利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算．
【详解】
解：它的侧面展开图的面积＝×2×2×3＝6（cm2）．
故选：B．
【点睛】
本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
6、B
【分析】
根据旋转可得，，得．
【详解】
解：，，
，
将绕点逆时针旋转得到△，使点的对应点恰好落在边上，
，，
．
故选：B．
【点睛】
本题考查了旋转的性质，等腰三角形的性质，三角形内角和定理，解决本题的关键是掌握旋转的性质．
7、C
【分析】
连接，根据垂径定理可得，设的半径为，则,进而勾股定理列出方程求得半径，进而求得
【详解】
解：如图，连接，
∵是的直径，弦，
∴
设的半径为，则
在中，，
即
解得
即
故选C
【点睛】
本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
8、D
【分析】
将绕点逆时针旋转得，根据旋转的性质得，，，则为等边三角形，得到，，在中，，，，根据勾股定理的逆定理可得到为直角三角形，且，即可得到的度数．
【详解】
解：为等边三角形，
，
可将绕点逆时针旋转得，
如图，连接，
，，，
为等边三角形，
，，
在中，，，，
，
为直角三角形，且，
．
故选：D．
【点睛】
本题考查了旋转的性质、等边三角形，解题的关键是掌握旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．
9、C
【分析】
由OA=OB，，求出∠AOB=130°，根据圆周角定理求出的度数．
【详解】
解：∵OA=OB，，
∴∠BAO=．
∴∠AOB=130°．
∴=∠AOB=65°．
故选：C．
【点睛】
此题考查了同圆中半径相等的性质，圆周角定理：同弧所对的圆周角等于圆心角的一半．
10、B
【分析】
根据关于原点对称的两个点，横坐标、纵坐标分别互为相反数，即可求解．
【详解】
解：平面直角坐标系中点关于原点对称的点的坐标是
故选B
【点睛】
本题考查了关于原点对称的点的特征，掌握关于原点对称的两个点，横坐标、纵坐标分别互为相反数是解题的关键．
二、填空题
1、
【分析】
连接OC交AB于点D，再连接OA．根据轴对称的性质确定，OD=CD；再根据垂径定理确定AD=BD；再根据勾股定理求出AD的长度，进而即可求出AB的长度．
【详解】
解：如下图所示，连接OC交AB于点D，再连接OA．
∵折叠后弧的中点与圆心重叠，
∴，OD=CD．
∴AD=BD．
∵圆形纸片的半径为10cm，
∴OA=OC=10cm．
∴OD=5cm．
∴cm．
∴BD=cm．
∴cm．
故答案为：．
【点睛】
本题考查轴对称的性质，垂径定理，勾股定理，综合应用这些知识点是解题关键．
2、
【分析】
先求出A、B、C坐标，再证明三角形BOC是等边三角形，最后根据扇形面积公式计算即可．
【详解】
过C作CD⊥OA于D
∵一次函数的图象与x轴交于点A，与y轴交于点B，
∴当时，，B点坐标为（0,1）
当时，，A点坐标为
∴
∵作的外接圆，
∴线段AB中点C的坐标为,
∴三角形BOC是等边三角形
∴
∵C的坐标为
∴
∴
故答案为：
【点睛】
本题主要考查了一次函数的综合运用，求扇形面积．用已知点的坐标表示相应的线段是解题的关键．
3、140
【分析】
作的外接圆，根据三角形内心的性质可得：，，再由三角形内角和定理得出：，最后根据三角形外心的性质及圆周角定理即可得．
【详解】
解：如图所示，作的外接圆，
∵点I是的内心，
∴BI，CI分别平分和，
∴，，
∵，
∴，
∴，
∴，
∵点O是的外心，
∴，
故答案为：140．
【点睛】
题目主要考查三角形内心与外心的性质，三角形内角和定理等，理解题意，熟练掌握三角形内心与外心的性质是解题关键．
4、
【分析】
如图，作BH⊥x轴于H．由△ACO≌△BAH（AAS），推出BH＝OA＝m，AH＝OC＝4，可得B（m+4，m），令x＝m+4，y＝m，推出y＝x﹣4，推出点B在直线y＝x﹣4上运动，设直线y＝x﹣4交x轴于E，交y轴于F，作KM⊥EF于M，根据垂线段最短可知，当点B与点M重合时，BK的值最小，利用等腰直角三角形的性质可得M的坐标，从而可得答案．
【详解】
解：如图，作BH⊥x轴于H．
∵C（0，4），K（2，0），
∴OC＝4，OK＝2，
∵AC＝AB，∵∠AOC＝∠CAB＝∠AHB＝90°，
∴∠CAO+∠OCA＝90°，∠BAH+∠CAO＝90°，
∴∠ACO＝∠BAH，
∴△ACO≌△BAH（AAS），
∴BH＝OA＝m，AH＝OC＝4，
∴B（m+4，m），
令x＝m+4，y＝m，
∴y＝x﹣4，
∴点B在直线y＝x﹣4上运动，设直线y＝x﹣4交x轴于E，交y轴于F，
则

作KM⊥EF于M，过作于 则
根据垂线段最短可知，当点B与点M重合时，BK的值最小，此时B（3，﹣1），
故答案为：（3，﹣1）
【点睛】
本题考查坐标与图形的变化﹣旋转，全等三角形的判定和性质，一次函数的应用，垂线段最短等知识，解题的关键是正确寻找点B的运动轨迹，学会利用垂线段最短解决最短问题．
5、60
【分析】
根据弧长公式求解即可．
【详解】
解：，
解得，，
故答案为：60．
【点睛】
本题考查了弧长公式，灵活应用弧长公式是解题的关键.
三、解答题
1、见解析
【分析】
先作线段的垂直平分线．确定的中点，再以中点为圆心，一半为半径作圆交于点，然后作直线，则根据圆周角定理可得为所求．
【详解】
如图，直线AB就是所求作的，
（作法不唯一，作出一条即可，需要有作图痕迹）
【点睛】
本题考查了作图复杂作图，解题的关键是掌握复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
2、（1）图见解析；（2）直径所对的圆周角是直角，切线的判定定理
【分析】
（1）根据所给的几何语言作出对应的图形即可；
（2）根据圆周角定理和切线的判定定理解答即可．
【详解】
解：（1）补全图形如图所示，直线AP即为所求作；
（2）证明：连接BA，
由作法可知，
∴点A在以OP为直径的圆上，
∴（直径所对的圆周角是直角），
∵OA是的半径，
∴直线PA与相切（切线的判定定理），
故答案为：直径所对的圆周角是直角，切线的判定定理．
【点睛】
本题考查基本作图-画圆、圆周角定理、切线的判定定理，熟知复杂作图是在基本作图的基础上进行作图，一般是结合几何图形的性质，因此熟练掌握基本图形的性质和切线的判定是解答的关键．
3、（1）见详解；（2）
【分析】
（1）连接OD，由圆周角定理可得∠AOD=∠ABC，从而得OD∥BC，进而即可得到结论；
（2）连接AC，交OD于点F，利用勾股定理可得AC，，再证明四边形DFCE是矩形，进而即可求解．
【详解】
（1）证明：连接OD，
∵是的中点，
∴∠ABC=2∠ABD，
∵∠AOD=2∠ABD，
∴∠AOD=∠ABC，
∴OD∥BC，
∵，
∴，
∴是的切线；
（2）连接AC，交OD于点F，
∵AB是直径，
∴∠ACB=90°，
∴AC=，
∵是的中点，
∴OD⊥AC，AF=CF=3，
∴，
∴DF=5-4=1，
∵∠E=∠EDF=∠DFC=90°，
∴四边形DFCE是矩形，
∴DE=CF=3，CE=DF=1，
∴，
∴AD=CD=，
∵∠ADB=90°，
∴
【点睛】
本题主要考查切线的判定定理，圆周角定理以及勾股定理，添加辅助线构造直角三角形和矩形，是解题的关键．
4、（1） （2）PF=AB-PB或PF=AB+PB，理由见解析
【分析】
（1）根据△PBD等腰直角三角形，PB＝2，求出DB的长，由⊙O是△PBD的外接圆，∠DBE＝30°，可得答案；
（2）根据同弧所对的圆周角，可得∠ADP=∠FBP，由△PBD等腰直角三角形，得∠DPB=∠APD=90°，DP=BP，可证△APD≌△FPB，可得答案．
【详解】
解：（1）由题意画以下图，连接EP，
∵△PBD等腰直角三角形，⊙O是△PBD的外接圆，
∴∠DPB=∠DEB=90°，
∵PB＝2，
∴ ，
∵∠DBE＝30°，
∴
（2）①点P在点A、B之间，
由（1）的图根据同弧所对的圆周角相等，可得：
∠ADP=∠FBP，
又∵△PBD等腰直角三角形，
∴∠DPB=∠APD=90°，DP=BP，
在△APD和△FPB中
∴△APD≌△FPB
∴AP=FP，
∵AP+PB=AB
∴FP+PB=AB，
∴FP=AB-PB，
②点P在点B的右侧，如下图：
∵△PBD等腰直角三角形，
∴∠DPB=∠APF=90°，DP=BP，
∵∠PBF+∠EBP=180°，∠PDA+∠EBP=180°，
∴∠PBF=∠PDA，
在△APD和△FPB中
∴△APD≌△FPB
∴AP=FP，
∴AB+PB=AP，
∴AB+PB=PF，
∴PF= AB+PB．
综上所述，FP=AB-PB或PF= AB+PB．
【点睛】
本题考查了圆的性质，等腰直角三角形，三角形全等的判定，做题的关键是注意（2）的两种情况．
5、（1）见解析；（2）3
【分析】
（1）由题意连接OC，OB，由等边三角形的性质可得∠ABC=∠BCE=60°，求出∠OCB=30°，则∠OCE=90°，结论得证；
（2）根据题意由条件可得∠DBC=30°，∠BEC=90°，进而即可求出CE=BC＝3．
【详解】
解：（1）证明：如图连接OC、OB．
∵是等边三角形
∴
∵
∴
又 ∵
∴
∴
∴
∴与⊙O相切；
（2）∵四边形ABCD是⊙O的内接四边形，
∴
∴
∵D为的中点，
∴
∴
∵
∴
∴
【点睛】
本题主要考查等边三角形的性质、圆周角定理、圆内接四边形的性质、切线的判定以及直角三角形的性质等知识．解题的关键是正确作出辅助线，利用圆的性质进行求解．