沪科版九年级下册第26章 概率初步综合与测试同步训练题

这是一份沪科版九年级下册第26章 概率初步综合与测试同步训练题，共21页。
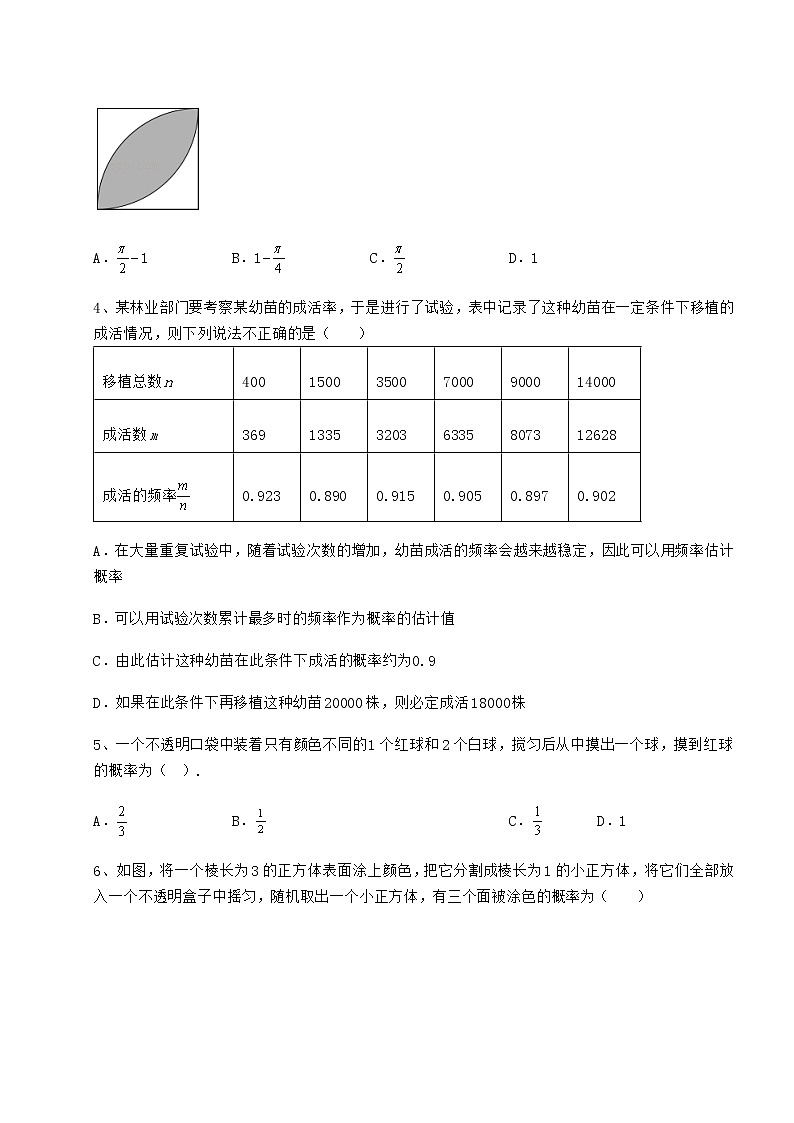
沪科版九年级数学下册第26章概率初步专项训练 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、下列说法中，正确的是（    ）A．“射击运动员射击一次，命中靶心”是必然事件B．事件发生的可能性越大，它的概率越接近1C．某种彩票中奖的概率是1%，因此买100张该种彩票就一定会中奖D．抛掷一枚图钉，“针尖朝上”的概率可以用列举法求得2、某学校九年级为庆祝建党一百周年举办“歌唱祖国”合唱比赛，用抽签的方式确定出场顺序．现有8根形状、大小完全相同的纸签，上面分别标有序号1、2、3、4、5、6、7、8．下列事件中是必然事件的是（    ）A．一班抽到的序号小于6 B．一班抽到的序号为9C．一班抽到的序号大于0 D．一班抽到的序号为73、若随意向如图所示的正方形内抛一粒石子，则石子落在阴影部分的概率是（　　）A．1 B．1 C． D．14、某林业部门要考察某幼苗的成活率，于是进行了试验，表中记录了这种幼苗在一定条件下移植的成活情况，则下列说法不正确的是（　　）移植总数n400150035007000900014000成活数m369133532036335807312628成活的频率0.9230.8900.9150.9050.8970.902A．在大量重复试验中，随着试验次数的增加，幼苗成活的频率会越来越稳定，因此可以用频率估计概率B．可以用试验次数累计最多时的频率作为概率的估计值C．由此估计这种幼苗在此条件下成活的概率约为0.9D．如果在此条件下再移植这种幼苗20000株，则必定成活18000株5、一个不透明口袋中装着只有颜色不同的1个红球和2个白球，搅匀后从中摸出一个球，摸到红球的概率为（　）.A．      B．             C．    D．16、如图，将一个棱长为3的正方体表面涂上颜色，把它分割成棱长为1的小正方体，将它们全部放入一个不透明盒子中摇匀，随机取出一个小正方体，有三个面被涂色的概率为（    ）A． B． C． D．7、任意掷一枚质地均匀的骰子，偶数点朝上的可能性是（    ）A． B． C． D．8、在一个不透明的口袋中装有3张完全相同的卡片，卡片上面分别写有数字，0，2，从中随机抽出两张不同卡片，则下列判断正确的是（      ）A．数字之和是0的概率为0 B．数字之和是正数的概率为C．卡片上面的数字之和是负数的概率为 D．数字之和分别是负数、0、正数的概率相同9、中国象棋文化历史久远．在图中所示的部分棋盘中，“馬”的位置在“”（图中虚线）的下方，“馬”移动一次能够到达的所有位置已用“●”标记，则“馬”随机移动一次，到达的位置在“”上方的概率是（   ）A． B． C． D．10、下列说法正确的是（   ）A．“买中奖率为的奖券10张，中奖”是必然事件B．“汽车累积行驶，出现一次故障”是随机事件C．襄阳气象局预报说“明天的降水概率为70%”，意味着襄阳明天一定下雨D．若两组数据的平均数相同，则方差大的更稳定第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、学校决定从甲、乙、丙三名学生中随机抽取两名介绍学习经验，则同时抽到乙、丙两名同学的概率为_____．2、某射击运动员在同一条件下的射击成绩记录如下：射击次数20401002004001000“射中9环以上”的次数153378158321801“射中9环以下”的频率      通过计算频率，估计这名运动员射击一次时“射中9环以上”的概率是______（结果保留小数点后一位）．3、从3，0，，，这五个数中，随机抽取一个数作为m的值，则使函数的图象经过一、三象限，且使关于x的方程有实数根的概率是__________．4、已如一个口袋中装有7个只有颜色不同的球，其中3个白球，4个黑球．若往口袋中再放入2个白球，求从口袋中随机取出一个白球的概率________5、现有四张分别标有数字﹣2，﹣1，0，2的卡片，它们除数字外完全相同．把卡片背面朝上洗匀，从中随机抽取一张，记下数字不放回，然后背面朝上洗匀，再随机抽取一张，则两次抽出的卡片上所标数字之和为正数的概率是 _____．三、解答题（5小题，每小题10分，共计50分）1、一个不透明的口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4随机摸取一个小球后，不放回，再随机摸出一个小球，分别求下列事件的概率：（1）两次取出的小球标号和为奇数；（2）两次取出的小球标号和为偶数．2、盲盒为消费市场注入了活力．某商家将1副单价为60元的蓝牙耳机、2个单价为40元的多接口优盘、1个单价为30元的迷你音箱分别放入4个外观相同的盲盒中．（1）如果随机抽一个盲盒，直接写出抽中多接口优盘的概率；（2）如果随机抽两个盲盒，求抽中总价值不低于80元商品的概率．3、在一个不透明的口袋中装有4个依次写有数字1，2，3，4的小球，它们除数字外都相同，每次摸球前都将小球摇匀．（1）从中随机摸出一个小球，上面的数字不小于2的概率为 　　．（2）从中随机摸出一球不放回，再随机摸出一球，请用列表或画树状图的方法，求两次摸出小球上的数字和恰好是奇数的概率．4、新年即将来临，利群商场为了吸引顾客，特别设计了一种促销活动：在一个不透明的箱子里放有4个除数字外完全相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）．商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费，某顾客刚好消费200元．（1）该顾客至少可得到     元购物券；（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于40元的概率．5、某水果公司以9元/千克的成本从果园购进10000千克特级柑橘，在运输过程中，有部分柑橘损坏，该公司对刚运到的特级柑橘进行随机抽查，并得到如下的“柑橘损坏率”统计图．由于市场调节，特级柑橘的售价与日销售量之间有一定的变化规律，如下表是近一段时间该水果公司的销售记录 特级柑橘的售价（元/千克）1415161718特级柑橘的日销售量（千克）1000950900850800 （1）估计购进的10000千克特级柑橘中完好的柑橘的总重量为_____千克；（2）按此市场调节的观律，①若特级柑橘的售价定为16.5元/千克，估计日销售量，并说明理由②考虑到该水果公司的储存条件，该公司打算12天内售完这批特级柑橘（只售完好的柑橘），且售价保持不变求该公司每日销售该特级柑橘可能达到的最大利润，并说明理由． -参考答案-一、单选题1、B【分析】根据随机事件，必然事件，不可能事件的定义可判断A，根据随机事件发生的机会大小，估计概率的大小可判断B，可判断C，不规则物体的概率只能通过大数次的实验，使频率达到稳定时用频率估计概率可判断D．【详解】解：“射击运动员射击一次，命中靶心”可能会发生，也可都能不会发生是随机事件不是必然事件，故选项A不正确；事件发生的可能性越大，说明发生的机会越大，它的概率越接近1，故选项B正确；某种彩票中奖的概率是1%，因此买100张该种彩票每一张彩票中奖的概率都是1%，可能会中奖，但一定会中奖机会很小，故选项C不正确；图钉是不规则的物体，抛掷一枚图钉，“针尖朝上”的概率只能通过实验，大数次的实验，使频率稳定时，可用频率估计概率，不可以用列举法求得，故选项D不正确．故选择B．【点睛】本题考查事件，事件发生的可能性，概率，实验概率，掌握事件，事件发生的可能性，概率，实验概率知识是解题关键．2、C【分析】必然事件，是指在一定条件下一定会发生的事件；根据必然事件的定义对几个选项进行判断，得出答案．【详解】解：A中一班抽到的序号小于是随机事件，故不符合要求；B中一班抽到的序号为是不可能事件，故不符合要求；C中一班抽到的序号大于是必然事件，故符合要求；D中一班抽到的序号为是随机事件，故不符合要求；故选C．【点睛】本题考察了必然事件．解题的关键在于区分必然、随机与不可能事件的含义．3、A【分析】设正方形ABCD的边长为a，然后根据石子落在阴影部分的概率即为阴影部分面积与正方形面积的比，由此进行求解即可．【详解】解：如图所示，设正方形ABCD的边长为a，∵四边形ABCD是正方形，∴∠C=90°，∴ ，∴，∴石子落在阴影部分的概率是，故选A．【点睛】本题主要考查了几何概率，正方形的性质，扇形面积公式，解题的关键在于能够根据题意得到石子落在阴影部分的概率即为阴影部分面积与正方形面积的比．4、D【分析】根据频率估计概率逐项判断即可得．【详解】解：A．在大量重复试验中，随着试验次数的增加，幼苗成活的频率会越来越稳定，因此可以用频率估计概率，则此选项说法正确；B．可以用试验次数累计最多时的频率作为概率的估计值，则此选项说法正确；C．由此估计这种幼苗在此条件下成活的概率约为0.9，则此选项说法正确；D．如果在此条件下再移植这种幼苗20000株，则大约成活18000株，则此选项说法错误；故选：D．【点睛】本题考查了频率估计概率，掌握理解利用频率估计概率是解题关键．5、C【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．本题球的总数为1+2=3，红球的数目为1．【详解】解：根据题意可得：一个不透明口袋中装着只有颜色不同的1个红球和2个白球，共3个，任意摸出1个，摸到红球的概率是：1÷3=．故选：C．【点睛】本题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．6、B【分析】直接根据题意得出恰有三个面被涂色的有8个，再利用概率公式求出答案．【详解】解：由题意可得：小立方体一共有27个，恰有三个面被涂色的为棱长为3的正方体顶点处的8个小正方体；故取得的小正方体恰有三个面被涂色．的概率为．故选：B．【点睛】此题主要考查了概率公式的应用，正确得出三个面被涂色．小立方体的个数是解题关键．7、A【分析】如果一个事件的发生有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率 利用概率公式直接计算即可得到答案．【详解】解：抛掷一枚分别标有1，2，3，4，5，6的正方体骰子，骰子落地时朝上的数为偶数的可能性有种，而所有的等可能的结果数有种，所以骰子落地时朝上的数为偶数的概率是  故选A【点睛】本题考查了简单随机事件的概率，掌握概率公式是解本题的关键.8、A【分析】列树状图，得到共有6种等可能的情况，和为正数的有4种情况，和为负数的有2种情况，依次判断即可．【详解】解：列树状图如下：共有6种等可能的情况，和为正数的有4种情况，和为负数的有2种情况，A. 数字之和是0的概率为0，故该项符合题意；    B. 数字之和是正数的概率为，故该项不符合题意； C. 卡片上面的数字之和是负数的概率为，故该项不符合题意； D. 数字之和分别是负数、0、正数的概率不相同，故该项不符合题意； 故选：A．【点睛】此题考查了列树状图求事件的概率，概率的计算公式，正确列出树状图解答是解题的关键．9、C【分析】用“---”（图中虚线）的上方的黑点个数除以所有黑点的个数即可求得答案．【详解】解：观察“馬”移动一次能够到达的所有位置，即用“●”标记的有8处，位于“---”（图中虚线）的上方的有2处，所以“馬”随机移动一次，到达的位置在“---”上方的概率是，故选：C．【点睛】本题考查概率的求法与运用，一般方法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．10、B【分析】根据随机事件的概念、概率的意义和方差的意义分别对每一项进行分析，即可得出答案．【详解】解：A、“买中奖率为的奖券10张，中奖”是随机事件，故本选项错误；B、汽车累积行驶10000km，出现一次故障”是随机事件，故本选项正确；C、襄阳气象局预报说“明天的降水概率为70%”，意味着明天可能下雨，故本选项错误；D、若两组数据的平均数相同，则方差小的更稳定，故本选项错误；故选：B．【点睛】此题考查了随机事件、概率的意义和方差的意义，正确理解概率的意义是解题的关键．二、填空题1、【分析】画树状图，共有6种等可能的结果，同时抽到乙、丙两名同学的结果有2个，再由概率公式解题．【详解】解：画树状图如图：共有6个等可能的结果，同时抽到乙、丙两名同学的结果有2个，∴同时抽到乙、丙两名同学的概率为，故答案为：．【点睛】本题考查列树状图表示概率，是重要考点，掌握相关知识是解题关键．2、0.8【分析】重复试验次数越多，其频率越能估计概率，求出射击1000次时的频率即可．【详解】解：由题意可知射击1000次时，运动员射击一次时“射中9环以上”的频率为∴用频率估计概率为0.801，保留小数点后一位可知概率值为0.8故答案为：0.8．【点睛】本题考查了概率．解题的关键在于明确频率估计概率时要在重复试验次数尽可能多的情况下．3、【分析】由正比例函数的图象及其性质可判断3，0，，，五个数均符合，由一元二次方程根的判别式可判断出只有，，三个数符合题意，故概率为．【详解】∵的图象经过一、三象限∴即3，0，，，这五个数均符合关于x的方程其中则令解得时关于x的方程有实数根故，，三个数符合题意则P=．故答案为：．【点睛】本题考查了正比例函数图象及其性质和一元二次方程根的判别式．当时正比例函数图象过第一、三象限，时正比例函数图象过第二、四象限；使用一元二次方程根的判别式，应先将方程整理成一般形式，再确定a，b，c的值．注意利用判别式可以判断方程的根的情况，反之，当方程有两个不相等的实数根时，；有两个相等的实数根时，；没有实数根时，．当时，方程有两个相等的实数根，不能说方程只有一个根．4、【分析】先确定口袋中的球数，任意取出一个，求出等可能的所有情况，再从中找出满足条件的白球的可能情况，让后利用概率公式计算即可．【详解】解：往口袋中再放入2个白球，此时口袋中一共有球9个，任取一个球出现等可能情况一共有9中可能，其中有白球5个，任取一个球是白球的共有5中情况，∴从口袋中随机取出一个白球的概率P=，故答案为：．【点睛】本题考查列举法求简单概率，掌握列举法求简单概率，抓住列举所有等可能情况，与满足条件的情况，记住概率公式是解题关键．5、【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次抽出的卡片所标数字之和为正数的情况，再利用概率公式即可求得答案．【详解】解：画树状图如下所示：由树状图可知，一共有16中等可能性的结果数，其中两次抽出的卡片上所标数字之和为正数的结果数有（-1,2），（0，2），（2，-1），（2，0）四种情况，∴P两次抽出的卡片上所标数字之和为正数，故答案为：．【点睛】本题主要考查了列表法或树状图法求概率．解题的关键在于能够熟练掌握：概率=所求情况数与总情况数之比．三、解答题1、（1）；（2）．【分析】（1）列出表格展示所有可能的结果，根据表格即可知共有12种可能的情况，再找到两次取出的小球标号和为奇数的情况数，利用概率公式，即可求解；（2）找出两次取出的小球标号和为偶数的情况数，再利用概率公式，即可求解．（1）解：根据题意列出表格，如下表：根据表格可知：共有12种可能的情况，其中两次取出的小球标号和为奇数的情况有8种，故两次取出的小球标号和为奇数的概率为；（2）根据表格可知：两次取出的小球标号和为偶数的情况有4种．故两次取出的小球标号和为偶数的概率为． 12341 1+2=3，奇数1+3=4，偶数1+4=5，奇数22+1=3，奇数 2+3=5，奇数2+4=6，偶数33+1=4，偶数3+2=5，奇数 3+4=7，奇数44+1=5，奇数4+2=6，偶数4+3=7，奇数 【点睛】2、（1）抽中多接口优盘的概率为；（2）P（抽中商品总价值不低于80元）．【分析】（1）利用列举法求解即可；（2）先用列表法或树状图法得出所有的等可能的结果数，然后找到总价值不低于80元商品的结果数，最后根据概率公式求解即可．【详解】解：（1）∵随机抽取一个盲盒可以抽到蓝牙耳机，多接口优盘1，多接口优盘2，迷你音箱，一共4种等可能性的结果，其中抽到多接口优盘的结果数有2种，∴抽到多接口优盘；（2）将蓝牙耳机记为A，多接口U盘记为、，迷你音箱记作C．则从4个盲盒中随机抽取2个的树状图如下：由上图可知，随机抽两个盲盒，所获商品可能出现的结果有12种，它们出现的可能性相等，其中抽中商品总价值不低于80元的结果有8种．∴P（抽中商品总价值不低于80元）．【点睛】本题主要考查了列举法求解概率，树状图或列表法求解概率，解题的关键在于能够熟练掌握相关知识进行求解．3、（1）；（2）【分析】（1）列表确定出所有等可能的情况数，找出小球上写的数字不小于2的情况数，即可求出所求概率；（2）列表确定出所有等可能的情况数，找出两次摸出小球上的数字和恰好是奇数的情况数，即可求出所求概率．【详解】解：（1）从中随机摸出一个小球，小球上写的数字所有等可能情况有：1，2，3，4，共4种，其中数字不小于2的情况有：2，3，4，共3种，则P（小球上写的数字不小于2）＝；故答案为：；（2）根据题意列表得： 12341﹣﹣﹣（1，2）（1，3）（1，4）2（2，1）﹣﹣﹣（2，3）（2，4）3（3，1）（3，2）﹣﹣﹣（3，4）4（4，1）（4，2）（4，3）﹣﹣﹣所有等可能的数有12种，两次摸出小球上的数字和恰好是奇数的情况有8种，则P（两次摸出小球上的数字和恰好是奇数）＝＝．故答案为：【点睛】本题考查了概率公式，学会利用列表法与树状图法求随机事件的概率是解本题的关键．4、（1）10；（2）列表见解析，【分析】（1）根据小球上标的金额数找出最小的两个数，然后相加即可得出答案；（2）根据题意列出图表得出所有等可能的情况数和该顾客所获得购物券的金额高于40元的情况数，然后根据概率公式即可得出答案．【详解】解：（1）根据题意知，该顾客可能摸出金额最小的两个球是“0元”、“10元”，故至少可得到10元购物券，故答案为：10；（2）根据题意列表如下： 01020300\（0，10）（0，20）（0，30）10（10，0）\（10，20）（10，30）20（20，0）（20，10）\（20，30）30（30，0）（30，10）（30，20）\从上表可以看出，共有12种等可能结果，其中该顾客所获得购物券的金额不低于40元的结果有4种结果，所以该顾客所获得购物券的金额不低于40元的概率为＝．【点睛】本题考查了树状图法或列表法求概率，解题的关键是正确画出树状图或表格，然后用符合条件的情况数m除以所有等可能发生的情况数n即可，即．5、（1）9000千克；（2）①当售价定为16.5元/千克，日销售量为875千克，理由见解析；②最大利润售价为19元/千克，每日的最大利润为7500元，理由见解析【分析】（1）根据图形即可得出柑橘损坏的概率，再用整体1减去柑橘损坏的概率即可得出柑橘完好的概率，根据所得出柑橘完好的概率乘以这批柑橘的总质量即可．（2）①根据表格求出销售量y与售价x的函数关系式，代入x=16.5计算即可；②12天内售完9000千克完好的柑橘，求出日最大销售量即可求出售价的范围，再根据利润=（售价-进价）×销售量求出利润与售价的函数关系式即可；【详解】（1）由图可知损坏率在0.1上下波动，并趋于稳定故所求为千克（2）①设销售量y与售价x的函数关系式为由题意可得函数图像过及两点得∴与的函数关系式为把代入，∴当售价定为16.5元/千克，日销售量为875千克②依题意得：12天内售完9000千克柑橘故日销售量至少为：（千克）∴解得设利润为w元，则∴对称轴为∴当时w随x的增大而增大∴当时销售利润最大，最大利润为（元）【点睛】此题考查了利用频率估计概率，以及二次函数销售利润问题．解题的关键是在图中得到必要的信息，求出柑橘损坏的概率；并利用等量关系：利润=（售价-进价）×销售量求出利润与售价的函数关系式．