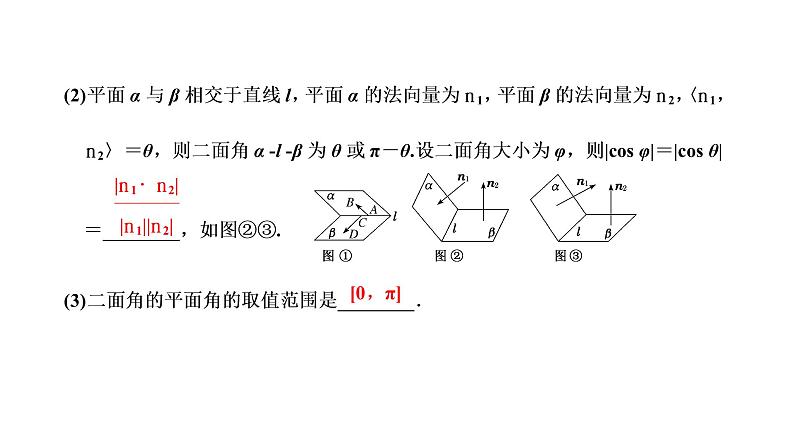
第七章 第七节 利用空间向量求空间角课件PPT

课时跟踪检测（四十五）  利用空间向量求空间角

[素养落实练]

1．把边长为2的正方形ABCD沿对角线BD折起，使得平面ABD⊥平面CBD，则异面直线AD，BC所成的角为(　　)

A．120°　　　　　　　　 B．30°

C．90°  D．60°

解析：选D　建立如图所示的空间直角坐标系，

则A(，0,0)，B(0，，0)，C(0，0，)，D(0，－，0)，

∴＝(－，－，0)，＝(0，－，)．

∴||＝2，||＝2，·＝2.

∴cos〈，〉＝＝＝.

∴异面直线AD，BC所成的角为60°.故选D.

2．在正方体ABCD ­A1B1C1D1中，点E为BB1的中点，则平面A1ED与平面ABCD所成的锐二面角的余弦值为(　　)

A.   B.

C.   D.

解析：选B　以A为坐标原点建立如图所示的空间直角坐标系A­xyz，

设棱长为1，

则A1(0,0,1)，E，D(0,1,0)，

∴＝(0,1，－1)，

＝，

设平面A1ED的一个法向量为n1＝(x，y，z)，

则即令x＝1，

∴∴n1＝(1,2,2)．

又平面ABCD的一个法向量为n2＝(0,0,1)，

∴cos〈n1，n2〉＝＝.

即平面A1ED与平面ABCD所成的锐二面角的余弦值为.

3．(2021·福州质检)已知四边形ABCD为正方形GD⊥平面ABCD，四边形DGEA与四边形DGFC也都为正方形，连接EF，FB，BE，H为BF的中点，有下述四个结论：

①DE⊥BF；②EF与CH所成角为；③EC⊥平面DBF；④BF与平面ACFE所成角为.

其中所有正确结论的编号是(　　)

A．①②  B．①②③

C．①③④  D．①②③④

解析：选B由题意得，所得几何体可以补形成一个正方体，如图所示．

以D为原点，DA，DC，DG所在直线分别为x，y，z轴，建立空间直角坐标系．

设AD＝DC＝DG＝2，

则D(0,0,0)，C(0,2,0)，E(2,0,2)，

F(0,2,2)，B(2,2,0)，H(1，2,1)．

①＝(2,0,2)，＝(－2,0,2)，

∴·＝－4＋0＋4＝0，

∴⊥，∴DE⊥BF，①是正确的．

②＝(－2,2,0)，＝(1,0,1)．

设EF与CH所成的角为θ，θ∈，

∴cos θ＝＝.

∵θ∈，∴θ＝，②是正确的．

③＝(－2,2，－2)，＝(2,2,0)，＝(0,2,2)．

设n＝(x，y，z)是平面DBF的一个法向量，

∴即取x＝1，∴n＝(1，－1,1)．

∵＝－2n，∴∥n，∴EC⊥平面DBF，③是正确的．

④＝(－2,0,2)，由图象易得m＝(1,1,0)是平面ACFE的一个法向量，

设BF与平面ACFE所成的角为θ，θ∈，

∴sin θ＝|cos〈，m〉|＝＝，∴θ＝，④是不正确的．

综上，①②③正确，故选B.

4．(多选)a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，则下列结论正确的是(　　)

A．当直线AB与a成60°角时，AB与b成30°角

B．当直线AB与a成60°角时，AB与b成60°角

C．直线AB与a所成角的最小值为45°

D．直线AB与a所成角的最小值为60°

解析：选BC　由题意知，a，b，AC三条直线两两相互垂直，设直线a，b的单位方向向量分别为a，b，将△ABC放入正方体中，画出图形如图所示．

不妨设图中所示正方体的棱长为1，则AC＝1，AB＝，

斜边AB以直线AC为旋转轴旋转，则A点保持不变，B点的运动轨迹是以C为圆心，1为半径的圆．以C为坐标原点，以CD所在直线为x轴，CB所在直线为y轴，CA所在直线为z轴，建立空间直角坐标系，

则D(1,0,0)，A(0,0,1)，直线a的单位方向向量a＝(0,1,0)，|a|＝1，直线b的单位方向向量b＝(1,0,0)，|b|＝1.

设B点在运动过程中的坐标为B′(cos θ，sin θ，0)，其中θ∈[0,2π)，

则＝(cos θ，sin θ，－1)，||＝.

设直线AB′与a所成的角为α，α∈，

则cos α＝＝|sin θ|∈，

所以α∈，所以C正确，D错误．

设直线AB′与b所成的角为β，β∈，

则cos β＝＝＝|cos θ|，

当直线AB′与a的夹角为60°时，α＝，|sin θ|＝cos α＝cos＝，

因为cos2θ＋sin2θ＝1，所以cos β＝|cos θ|＝.

因为β∈，所以β＝，即此时直线AB′与b的夹角为60°，所以B正确，A错误．

5．在直三棱柱ABC­A1B1C1中，AA1＝2，二面角B­AA1­C1的大小为60°，点B到平面ACC1A1的距离为，点C到平面ABB1A1的距离为2，则直线BC1与直线AB1所成角的正切值为________．

解析：由题意可知，∠BAC＝60°，点B到平面ACC1A1的距离为，点C到平面ABB1A1的距离为2，所以在三角形ABC中，AB＝2，AC＝4，BC＝2，∠ABC＝90°，

则·＝(－)·(＋)＝4，

||＝2，||＝4，

cos〈，〉＝＝，

故tan〈，〉＝.

答案：

6.如图，菱形ABCD中，∠ABC＝60°，AC与BD相交于点O，AE⊥平面ABCD，CF∥AE，AB＝2，CF＝3.若直线OF与平面BED所成的角为45°，则AE＝________.

解析：如图，以O为坐标原点，以OA，OB所在直线分别为x轴，y轴，以过点O且平行于CF的直线为z轴建立空间直角坐标系．

设AE＝a，则B(0，，0)，D(0，－，0)，F(－1,0,3)，E(1,0，a)，

∴＝(－1,0,3)，＝(0,2，0)，＝(－1，，－a)．

设平面BED的法向量为n＝(x，y，z)，

则即

则y＝0，令z＝1，得x＝－a，∴n＝(－a,0,1)，

∴cos〈n，〉＝＝.

∵直线OF与平面BED所成角的大小为45°，

∴＝，

解得a＝2或a＝－(舍去)，∴AE＝2.

答案：2

7．(2019·全国卷Ⅰ)如图，直四棱柱ABCD ­A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，N分别是BC，BB1，A1D的中点．

(1)证明：MN∥平面C1DE；

(2)求二面角A­MA1­N的正弦值．

解：(1)证明：如图，连接B1C，ME.

因为M，E分别为BB1，BC的中点，

所以ME∥B1C，且ME＝B1C.

又因为N为A1D的中点，所以ND＝A1D.

由题设知A1B1綊DC，

可得B1C綊A1D，故ME綊ND，

因此四边形MNDE为平行四边形，

所以MN∥ED.

又MN⊄平面C1DE，

所以MN∥平面C1DE.

(2)由已知可得DE⊥DA，以D为坐标原点，的方向为x轴正方向，建立如图所示的空间直角坐标系D ­ xyz，则A(2,0,0)，A1(2,0,4)，M(1，，2)，N(1,0,2)，

＝(0,0，－4)，＝(－1，，－2)，＝(－1,0，－2)，＝(0，－，0)．

设m＝(x，y，z)为平面A1MA的法向量，

则所以

可取m＝(，1,0)．

设n＝(p，q，r)为平面A1MN的法向量，

则所以

可取n＝(2,0，－1)．

于是cos〈m，n〉＝＝＝，

所以二面角A­MA1­N的正弦值为.

8．(2021·河北五校联考)如图所示，四边形ABCD与BDEF均为菱形，FA＝FC，且∠DAB＝∠DBF＝60°.

(1)求证：AC⊥平面BDEF；

(2)求直线AD与平面ABF所成角的正弦值．

解：(1)证明：设AC与BD相交于点O，连接FO，

∵四边形ABCD为菱形，∴AC⊥BD，且O为AC的中点，

∵FA＝FC，∴AC⊥FO，

又FO∩BD＝O，∴AC⊥平面BDEF.

(2)连接DF，∵四边形BDEF为菱形，且∠DBF＝60°，

∴△DBF为等边三角形．

∵O为BD的中点，

∴FO⊥BD，

又AC⊥FO，AC∩BD＝O，

∴FO⊥平面ABCD.

∵OA，OB，OF两两垂直，

∴建立空间直角坐标系O­xyz，如图所示，

设AB＝2，∵四边形ABCD为菱形，∠DAB＝60°，

∴BD＝2，AO＝，则AC＝2.

∵△DBF为等边三角形，∴OF＝.

∴A(，0,0)，B(0,1,0)，D(0，－1,0)，F(0,0，)，

∴＝(－，－1,0)，＝(－，0, )，＝(－，1,0)．

设平面ABF的法向量为n＝(x，y，z)，

则

取x＝1，得n＝(1，，1)．

设直线AD与平面ABF所成角为θ，

则sin θ＝|cos〈，n〉|＝＝.

∴直线AD与平面ABF所成角的正弦值为.

[梯度拔高练]

1．(2020·天津高考)如图，在三棱柱ABC­A1B1C1中，CC1⊥平面ABC，AC⊥BC，AC＝BC＝2，CC1＝3，点D，E分别在棱AA1和棱CC1上，且AD＝1，CE＝2，M为棱A1B1的中点．

(1)求证：C1M⊥B1D；

(2)求二面角B­B1E­D的正弦值；

(3)求直线AB与平面DB1E所成角的正弦值．

解：依题意，以C为原点，分别以，，的方向为x轴，y轴，z轴的正方向建立空间直角坐标系(如图)，可得C(0,0,0)，A(2,0,0)，B(0,2,0)，C1(0,0,3)，A1(2,0,3)，B1(0,2,3)，D(2，0,1)，E(0,0,2)，M(1,1,3)．

(1)证明：依题意，＝(1,1,0)，

＝(2，－2，－2)，从而·＝2－2＋0＝0，所以C1M⊥B1D.

(2)依题意，＝(2,0,0)是平面BB1E的一个法向量，

＝(0,2,1)，＝(2,0，－1)．

设n＝(x，y，z)为平面DB1E的法向量，

则即

不妨设x＝1，可得n＝(1，－1,2)．

因此有cos〈，n〉＝＝，

于是sin〈，n〉＝.

所以二面角B­B1E­D的正弦值为.

(3)依题意，＝(－2,2,0)．

由(2)知n＝(1，－1,2)为平面DB1E的一个法向量，

于是cos〈，n〉＝＝－.

所以直线AB与平面DB1E所成角的正弦值为.

2.如图，四棱锥P­ABCD的底面为矩形，PA是该四棱锥的高，PB与平面PAD所成的角为45°，F是PB的中点，E是BC上的动点．

(1)证明：PE⊥AF；

(2)若BC＝2AB，PE与AB所成角的余弦值为，求二面角D­PE­B的余弦值．

解：(1)证明：由题可知AD，AB，AP两两垂直，且∠BPA＝45°，∴AP＝AB.以点A为坐标原点，AD，AB，AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系，如图．

设AP＝AB＝b，BE＝a，

则A(0,0,0)，B(0，b,0)，E(a，b,0)，P(0,0，b)，F，

∴＝(a，b，－b)，＝.

∴·＝0，∴PE⊥AF.

(2)设AP＝AB＝2，则BC＝4，

故D(4,0,0)，B(0,2,0)，E(a,2,0)，F(0,1,1)，P(0,0,2)，

∴＝(0,2,0)，＝(a,2，－2)，＝(0,1,1)．

由＝，得＝，

解得a＝3(负值舍去)，∴E(3,2,0)．

设平面PDE的一个法向量为n＝(x，y，z)，

又＝(4,0，－2)，＝(1，－2,0)，

∴得令y＝1，得n＝(2,1,4)．

∵·＝0，∴AF⊥PB.

又由(1)知AF⊥PE，PB∩PE＝P，

∴AF⊥平面PBC，即为平面PBC的一个法向量．

设二面角D­PE­B的平面角为θ，由图可知θ为钝角，

∴cos θ＝－＝－＝－.

∴二面角D­PE­B的余弦值为－.