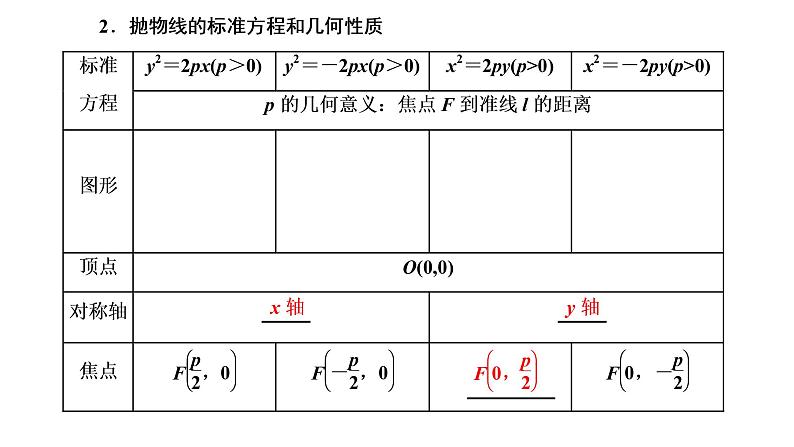
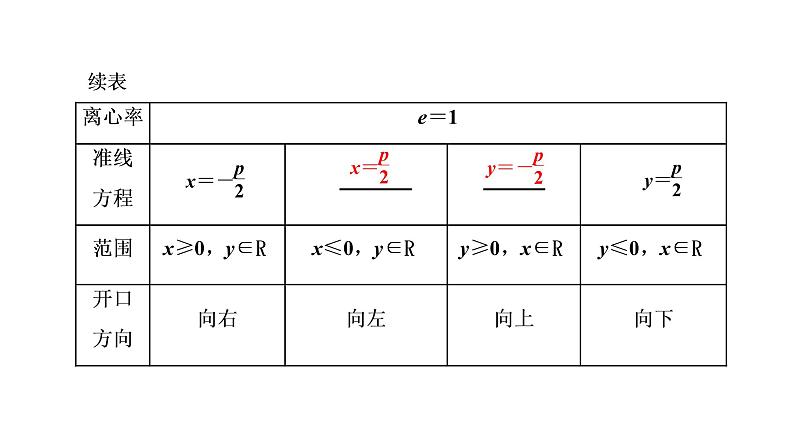
第八章 第七节 抛物线课件PPT

这是一份第八章 第七节 抛物线课件PPT，文件包含第七节抛物线ppt、课时跟踪检测五十四抛物线doc等2份课件配套教学资源，其中PPT共55页， 欢迎下载使用。
课时跟踪检测（五十四）  抛物线[素养落实练]1．若抛物线y2＝mx的焦点到顶点的距离为，则m＝(　　)A．2　　　　　　　　 　  B．4C．±2  D．±4解析：选C　由题意得＝1，m＝±2.2．若抛物线x2＝4y上的点P(m，n)到其焦点的距离为5，则n＝(　　)A.  B.C．3  D．4解析： 选D　抛物线x2＝4y的准线方程为y＝－1，根据抛物线的定义可知，5＝n＋1，得n＝4，故选D.3．(多选)已知F是抛物线C：y2＝16x的焦点，M是C上一点，FM的延长线交y轴于点N.若M为FN的中点，则(　　)A．C的准线方程为x＝－4B．F点的坐标为(0,4)C．|FN|＝12D．三角形ONF的面积为16(O为坐标原点)解析：选ACD　如图，不妨设点M位于第一象限，设抛物线的准线l与x轴交于点F′，作MB⊥l于点B，NA⊥l于点A.由抛物线的解析式可得准线方程为x＝－4，F点的坐标为(4,0)，则|AN|＝4，|FF′|＝8.在直角梯形ANFF′中，中位线|MB|＝＝6，由抛物线的定义有|MF|＝|MB|＝6，结合题意，有|MN|＝|MF|＝6，故|FN|＝|MF|＋|MN|＝6＋6＝12，|ON|＝＝8，S△ONF＝×8×4＝16.故选A、C、D.4．圆O：x2＋y2＝r2与抛物线Γ：y2＝4x交于A，B两点，与Γ的准线交于C，D两点，若四边形ABCD为矩形，则该矩形的面积为(　　)A．2  B．4C．8  D．16解析：选C　因为CD在准线上，根据矩形的对称性可得AB过焦点F，则|AF|＝|DA|且AF⊥x轴，所以A(1，±2)，故|AF|＝|DA|＝2，从而|AB|＝4，故矩形的面积为2×4＝8.5．(2020·全国卷Ⅲ)设O为坐标原点，直线x＝2与抛物线C：y2＝2px(p>0)交于D，E两点，若OD⊥OE，则C的焦点坐标为(　　)A.  B.C．(1,0)  D．(2,0)解析：选B　将直线方程与抛物线方程联立，可得y＝±2，不妨设D(2,2)，E(2，－2)．由OD⊥OE，可得·＝4－4p＝0，解得p＝1，所以抛物线C的方程为y2＝2x，其焦点坐标为.6．已知抛物线C：y2＝2px(p>0)，过焦点F且斜率为 的直线与C相交于P，Q两点，且P，Q两点在准线上的射影分别为M，N两点，则S△MFN等于(　　)A.p2  B.p2C.p2   D.p2解析：选B　不妨设P在第一象限，过Q作QR⊥PM，垂足为R，设准线与x轴的交点为E，如图．∵直线PQ的斜率为，∴直线PQ的倾斜角为60°.由抛物线焦点弦的性质可得|PQ|＝|PF|＋|QF|＝＋＝＝p.在Rt△PRQ中，sin∠RPQ＝，∴|QR|＝|PQ|·sin∠RPQ＝p×＝p，由题意可知|MN|＝|QR|＝p，∴S△MFN＝|MN|·|FE|＝×p×p＝p2.故选B.7．已知抛物线C的方程为y2＝2px(p>0)，圆M的方程为x2＋y2＋8x＋12＝0，如果抛物线C的准线与圆M相切，那么p的值为________．解析：将圆M的方程化为标准方程：(x＋4)2＋y2＝4，圆心坐标为(－4,0)，半径r＝2，因为抛物线的准线方程为x＝－，所以＝2，解得p＝12或4.答案：12或48．已知点A(0,1)，抛物线C：y2＝ax(a＞0)的焦点为F，连接FA，与抛物线C相交于点M，延长FA，与抛物线C的准线相交于点N，若|FM|∶|MN|＝1∶2，则实数a的值为______．解析：依题意得抛物线的焦点F的坐标为，过M作抛物线的准线的垂线，垂足为K，由抛物线的定义知|MF|＝|MK|.因为|FM|∶|MN|＝1∶2，所以|KN|∶|KM|＝∶1，又kFN＝＝－，kFN＝－＝－，所以－＝－，解得a＝.答案：9．(2021·成都测试)已知抛物线C：y2＝2px(p>0)的焦点为F，准线为l，过点F作倾斜角为120°的直线与准线l相交于点A，线段AF与抛物线C相交于点B，且|AB|＝，则抛物线C的标准方程为________．解析：如图，设直线l与x轴交于点D，过点B作BE⊥l于点E，则|DF|＝p.因为直线AF的倾斜角为120°，所以∠AFD＝∠ABE＝60°，所以∠EAB＝30°.因为|AB|＝，所以|BE|＝|AB|＝.由抛物线的定义知|BE|＝|BF|，所以|AF|＝|AB|＋|BF|＝|AB|＋|BE|＝2，所以|DF|＝|AF|＝1，即p＝1，所以抛物线C的标准方程为y2＝2x.答案：y2＝2x10．设抛物线y2＝4x的焦点为F，过点M(，0)的直线与抛物线相交于A，B两点，与抛物线的准线相交于C点，|BF|＝3，则△BCF与△ACF的面积之比＝________.解析：设点A在第一象限，B在第四象限，A(x1，y1)，B(x2，y2)，直线AB的方程为x＝my＋.由y2＝4x，得p＝2，因为|BF|＝3＝x2＋＝x2＋1，所以x2＝2，则y＝4x2＝4×2＝8，所以y2＝－2，由得y2－4my－4＝0，则y1y2＝－4，所以y1＝，由y＝4x1，得x1＝.过点A作AA′垂直于准线x＝－1，垂足为A′，过点B作BB′垂直于准线x＝－1，垂足为B′，易知△CBB′∽△CAA′，所以＝＝.又|BB′|＝|BF|＝3，|AA′|＝x1＋＝＋1＝，所以＝＝.答案：11．(2021·昆明模拟)设抛物线C：x2＝2py(p＞0)的焦点为F，M(p，p－1)是C上的点．(1)求C的方程；(2)若直线l：y＝kx＋2与C交于A，B两点，且|AF|·|BF|＝13，求k的值．解：(1)因为M(p，p－1)是抛物线C上的点，所以p2＝2p(p－1)，因为p＞0，所以p＝2，因此抛物线C的方程为x2＝4y.(2)设点A(x1，y1)，B(x2，y2)，由得x2－4kx－8＝0，Δ＝16k2＋32＞0，则x1＋x2＝4k，x1x2＝－8.由抛物线的定义知，|AF|＝y1＋1＝kx1＋3，|BF|＝y2＋1＝kx2＋3，则|AF|·|BF|＝(kx1＋3)(kx2＋3)＝k2x1x2＋3k(x1＋x2)＋9＝4k2＋9＝13，解得k＝±1.12．已知抛物线C：y2＝3x的焦点为F，斜率为的直线l与C的交点为A，B，与x轴的交点为P.(1)若|AF|＋|BF|＝4，求l的方程；(2)若＝3，求|AB|.解：设直线l：y＝x＋t，A(x1，y1)，B(x2，y2)．(1)由题设得F，故|AF|＋|BF|＝x1＋x2＋.又|AF|＋|BF|＝4，所以x1＋x2＝.由可得9x2＋12(t－1)x＋4t2＝0，则x1＋x2＝－.从而－＝，得t＝－.所以l的方程为y＝x－.(2)由＝3可得y1＝－3y2.由可得y2－2y＋2t＝0，所以y1＋y2＝2，从而－3y2＋y2＝2，故y2＝－1，y1＝3.代入C的方程得x1＝3，x2＝.故|AB|＝. [梯度拔高练]1. (多选)如图，过点P(2,0)作两条直线x＝2和l：x＝my＋2(m>0)分别交抛物线y2＝2x于A，B和C，D(其中A，C位于x轴上方)，直线AC，BD交于点Q.则下列说法正确的是(　　)A．C，D两点的纵坐标之积为－4B．点Q在定直线x＝－2上C．点P与抛物线上各点的连线中，PA最短D．无论CD旋转到什么位置，始终有∠CQP＝∠BQP解析：选AB　设点C(x1，y1)，D(x2，y2)，将直线l的方程x＝my＋2代入抛物线方程y2＝2x得：y2－2my－4＝0.则y1y2＝－4，故A正确；由题得A(2,2)，B(2，－2)，直线AC的方程为y－2＝(x－2)，直线BD的方程为y＋2＝(x－2)，消去y得x＝，将y1y2＝－4代入上式得x＝－2，故点Q在直线x＝－2上，故B正确；设抛物线y2＝2x的任一点M的坐标为，则MP＝ ＝ .当a2＝2时，MP取得最小值，又PA＝2>，故C错误；因为PA＝PB，但QA≠QB，所以D错误．2．(2020·衡水质检)已知曲线C由抛物线y2＝2x及抛物线y2＝－2x组成，A(1,2)，B(－1,2)，M，N是曲线C上关于y轴对称的两点(A，B，M，N四点不共线，且点M在第一象限)，则四边形ABNM周长的最小值为(　　)A．2＋  B．1＋C．3  D．4解析：选B　设抛物线y2＝2x的焦点为F，则四边形ABNM的周长：l＝|AB|＋2|AM|＋2xM＝2＋2|AM|＋2|MF|－1≥1＋2|AF|＝1＋，当A，M，F共线时取等号． 3.如图，正方形ABCD和正方形DEFG的边长分别为a，b(a＜b)，原点O为AD的中点，抛物线y2＝2px(p＞0)经过C，F两点，则＝________.解析：依题知C，F，因为点C，F在抛物线上，所以两式相除得2－2－1＝0，解得＝1＋或＝1－(舍去)．答案：1＋4．已知直线y＝a交抛物线y＝x2于A，B两点．若该抛物线上存在点C，使得∠ACB为直角，则实数a的取值范围为________．解析：如图，设C(x0，x)(x≠a)，A(－，a)，B(，a)，则＝(－－x0，a－x)，＝(－x0，a－x)．∵CA⊥CB，∴·＝0，即－(a－x)＋(a－x)2＝0，(a－x)(－1＋a－x)＝0.∴x＝a－1≥0，∴a≥1.答案：[1，＋∞)5．(2020·全国卷Ⅱ)已知椭圆C1：＋＝1(a＞b＞0)的右焦点F与抛物线C2的焦点重合，C1的中心与C2的顶点重合．过F且与x轴垂直的直线交C1于A，B两点，交C2于C，D两点，且|CD|＝|AB|.(1)求C1的离心率；(2)设M是C1与C2的公共点．若|MF|＝5，求C1与C2的标准方程．解：(1)由已知可设C2的方程为y2＝4cx，其中c＝ .不妨设A，C在第一象限，由题设得A，B的纵坐标分别为，－；C，D的纵坐标分别为2c，－2c，所以|AB|＝，|CD|＝4c.由|CD|＝|AB|得4c＝，即3×＝2－22.解得＝或＝－2(舍去)．所以C1的离心率为.(2)由(1)知a＝2c，b＝c，故C1：＋＝1.设M(x0，y0)，则＋＝1，y＝4cx0，所以＋＝1. ①由于C2的准线为x＝－c，所以|MF|＝x0＋c，而|MF|＝5，所以x0＝5－c.将上式代入①得＋＝1，即c2－2c－3＝0，解得c＝3或c＝－1(舍去)．所以C1的标准方程为＋＝1，C2的标准方程为y2＝12x.