





- 第八章 第六节 双曲线课件PPT 课件 29 次下载
- 第八章 第七节 抛物线课件PPT 课件 29 次下载
- 第八章 第八节第二课时 最值与范围、证明问题课件PPT 课件 27 次下载
- 第八章 第八节第三课时 定点、定值、存在性问题课件PPT 课件 27 次下载
- 第八章 第八节第四课时 圆锥曲线与圆、向量的综合课件PPT 课件 27 次下载
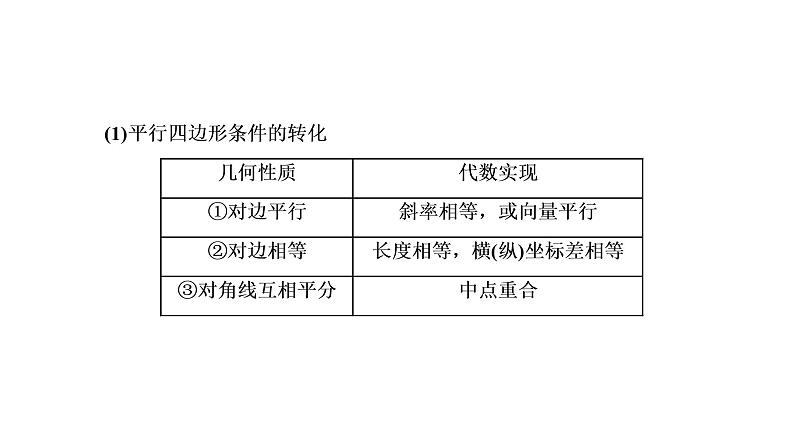
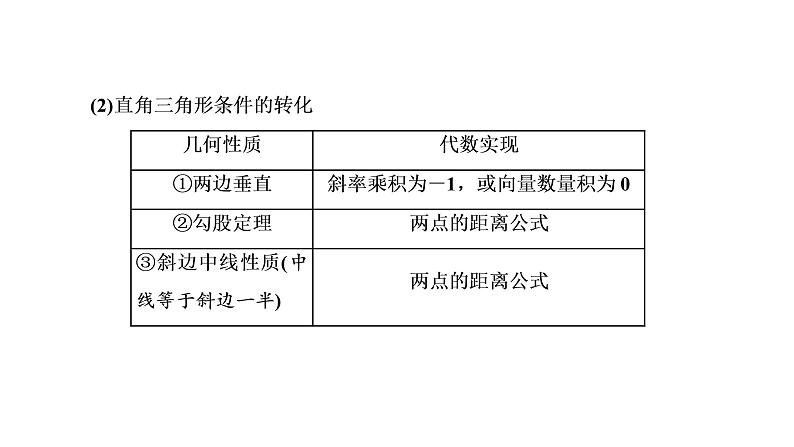
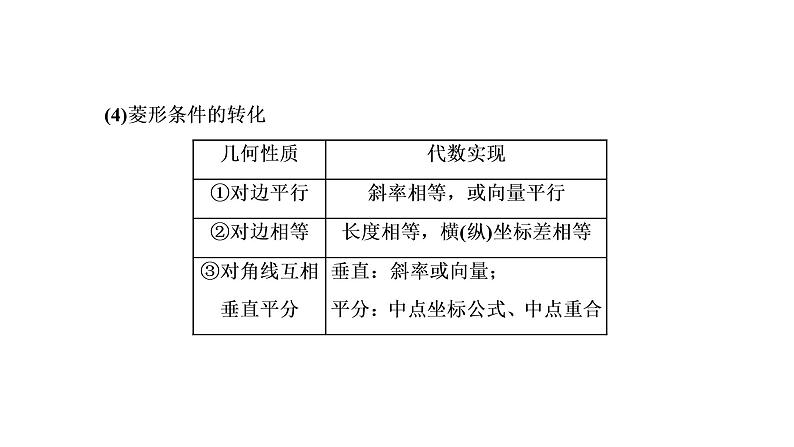
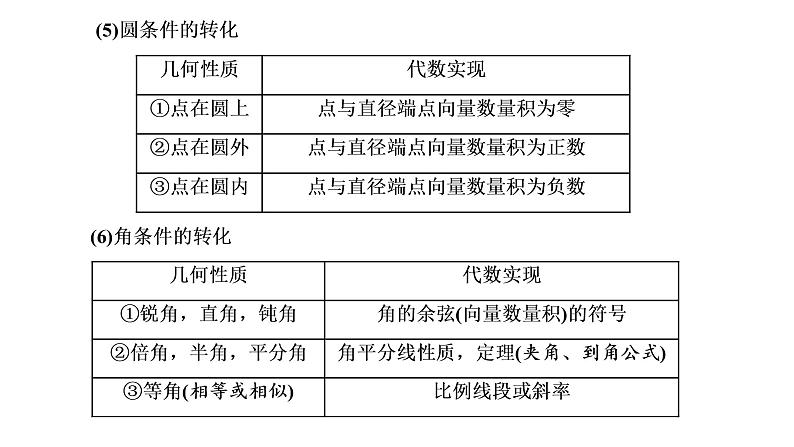
第八章 第八节第一课时 圆锥曲线几何特征的转化课件PPT
展开课时跟踪检测(五十五) 圆锥曲线几何特征的转化
1.已知椭圆M:+=1,点F1,C分别是椭圆M的左焦点、左顶点,过点F1的直线l(不与x轴重合)交椭圆M于A,B两点.
(1)求椭圆M的离心率及短轴长.
(2)问:是否存在直线l,使得点B在以线段AC为直径的圆上?若存在,求出直线l的方程;若不存在,请说明理由.
解:(1)由题意知,椭圆M的离心率e==,短轴长2b=2.
(2)设点B(x0,y0),由题意知点F1(-1,0),C(-2,0).
假设存在满足题意的直线l,则BC⊥BF1,
即BC·BF1=0,得(-2-x0,-y0)·(-1-x0,-y0)=0,即(x0+2)(x0+1)+y=0.①
又知点B(x0,y0)满足+=1. ②
联立①②,解得x0=-2或x0=-10.
由椭圆方程知,x0=-2或x0=-10均不满足题意,故舍去.
因此,不存在直线l,使得点B在以线段AC为直径的圆上.
2.已知动点P到直线l:x=4的距离是到点F(1,0)距离的2倍,记点P的轨迹为 曲线C.
(1)求曲线C的方程;
(2)记曲线C与x轴交于A,B两点,Q(4,0),设M是直线x=1上任意一点,直线MA,MB与曲线C的另一交点分别为D,E.求证:Q,D,E三点共线.
解:(1)动点P到直线l:x=4的距离是到点F(1,0)距离的2倍,设点P(x,y).
则=2,化简得+=1.
故曲线C的方程为+=1.
(2)证明:由(1)可得A(-2,0),B(2,0).设M(1,m).
直线MA的方程为y=(x+2),与椭圆方程+=1联立化简得(4m2+27)x2+16m2x+16m2-108=0.
则-2xD=,可得xD=,yD=.
同理可得:xE=,yE=.
∴kQD==-,kQE==-,
∴kQD=kQE.∴Q,D,E三点共线.
3.(2021·福州一模)已知椭圆C:+=1(a>b>0)的左焦点为F(-1,0),过F且垂直于x轴的直线被椭圆截得的弦长为3.
(1)求椭圆C的方程;
(2)已知点M(-4,0),过F作直线l交椭圆于A,B两点,证明:∠FMA=∠FMB.
解:(1)由题意可知c=1,把x=-1代入椭圆方程可得+=1,解得y=±,
∴=,又a2=b2+1,可得a=2,b=,
∴椭圆C的方程为+=1.
(2)证明:当直线l的斜率不存在时,由对称性可知:∠FMA=∠FMB.
当直线l的斜率存在时,设直线l的方程为y=k(x+1),
代入椭圆方程可得(3+4k2)x2+8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),
则x1+x2=,x1x2=,
∴kAM+kBM=+
=
=.
∵2x1x2+5(x1+x2)+8=-+8=0,
∴kAM+kBM=0,∴∠FMA=∠FMB.
综上,∠FMA=∠FMB.
4.(2021·北京西城区高三模拟)已知椭圆E:+=1(a>b>0)经过点C(0,1),离心率为.O为坐标原点.
(1)求椭圆E的方程;
(2)设A,B分别为椭圆E的左、右顶点,D为椭圆E上一点(不在坐标轴上),直线CD交x轴于点P,Q为直线AD上一点,且·=4,求证:C,B,Q三点共线.
解:(1)由题意,得b=1,=.
又a2=b2+c2,
所以a=2,c=.
故椭圆E的方程为+y2=1.
(2)证明:A(-2,0),B(2,0).
设D(x0,y0)(x0y0≠0),则+y=1.
因为C(0,1),所以直线CD的方程为y=x+1,
令y=0,得x=,故点P的坐标为.
设Q(xQ,yQ),由·=4,得xQ=(显然xQ≠±2).
直线AD的方程为y=(x+2),
将xQ代入直线AD的方程,得yQ=,
即Q.
显然直线BQ的斜率存在,
且kBQ==
===-.
又直线BC的斜率kBC=-,
所以kBC=kBQ,即C,B,Q三点共线.
5.已知抛物线C:y2=4x的焦点为F,直线l与抛物线C交于A,B两点,O是坐标原点.
(1)若直线l过点F且|AB|=8,求直线l的方程;
(2)已知点E(-2,0),若直线l不与坐标轴垂直,且∠AEO=∠BEO,证明:直线l过 定点.
解:(1)焦点F(1,0),显然直线l不垂直于x轴,设直线l的方程为x=my+1,
与y2=4x联立得y2-4my-4=0,
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4,
所以|AB|=
= =4(1+m2),
由|AB|=8,解得m=±1,
所以直线l的方程为y=x-1或y=-x+1.
(2)证明:设A(x1,y1),B(x2,y2),直线l的方程为x=my+b(m≠0),与y2=4x联立得y2-4my-4b=0,
可得y1+y2=4m,y1y2=-4b.
由∠AEO=∠BEO得kEA=-kEB,即=-,
整理得y1x2+2y1+x1y2+2y2=0,
即y1(my2+b)+2y1+(my1+b)y2+2y2=0,
整理得2my1y2+(b+2)(y1+y2)=0,
即-8bm+4(b+2)m=0,即b=2.
故直线l的方程为x=my+2,过定点(2,0).
备战2024高考一轮复习数学(理) 第九章 解析几何 第八节 直线与圆锥曲线的位置关系课件PPT: 这是一份备战2024高考一轮复习数学(理) 第九章 解析几何 第八节 直线与圆锥曲线的位置关系课件PPT,共30页。PPT课件主要包含了平行或重合,答案A,答案B,答案C等内容,欢迎下载使用。
第八章 第八节第四课时 圆锥曲线与圆、向量的综合课件PPT: 这是一份第八章 第八节第四课时 圆锥曲线与圆、向量的综合课件PPT,文件包含第八节第四课时圆锥曲线与圆向量的综合ppt、课时跟踪检测五十八圆锥曲线与圆向量的综合doc等2份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
第八章 第八节第二课时 最值与范围、证明问题课件PPT: 这是一份第八章 第八节第二课时 最值与范围、证明问题课件PPT,文件包含第八节第二课时最值与范围证明问题ppt、课时跟踪检测五十六最值与范围证明问题doc等2份课件配套教学资源,其中PPT共34页, 欢迎下载使用。












