广东省深圳市罗湖区2021-2022学年高三上学期期末考试数学试卷

这是一份广东省深圳市罗湖区2021-2022学年高三上学期期末考试数学试卷，文件包含高三数学第一学期期末试卷答案docx、高三数学第一学期期末试卷答案pdf、深圳市罗湖区高三数学第一学期期末试卷pdf等3份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
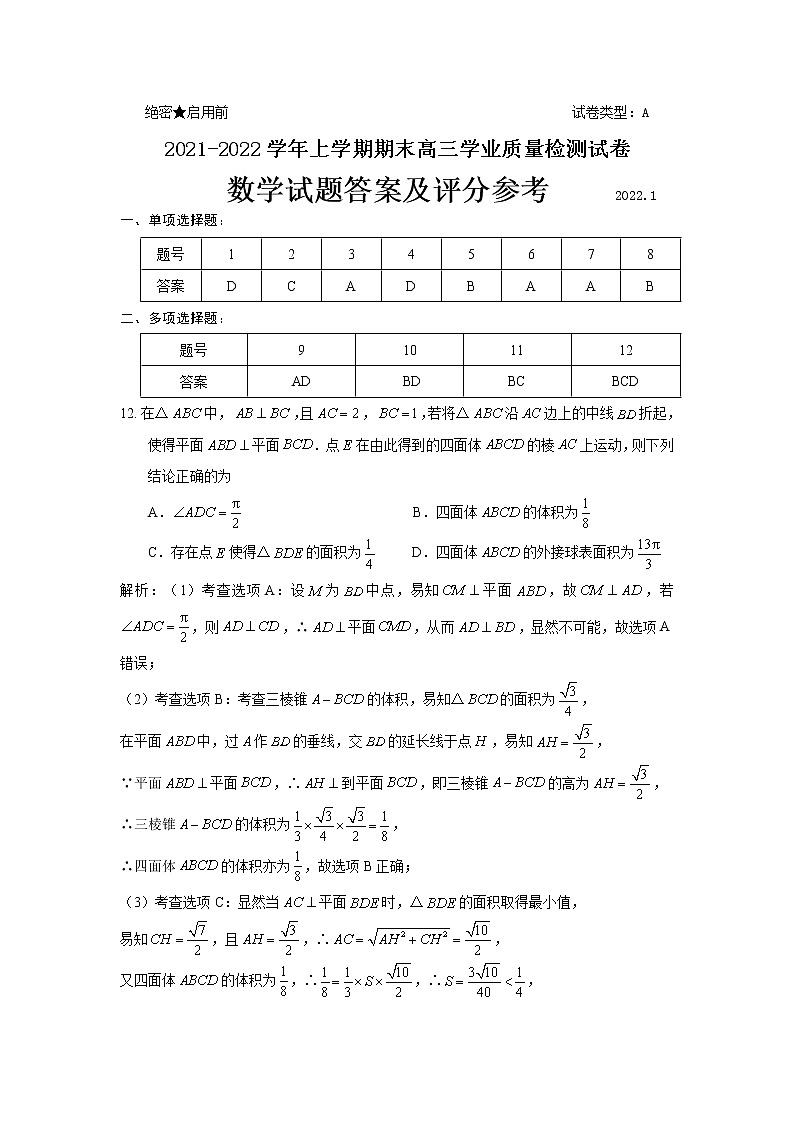
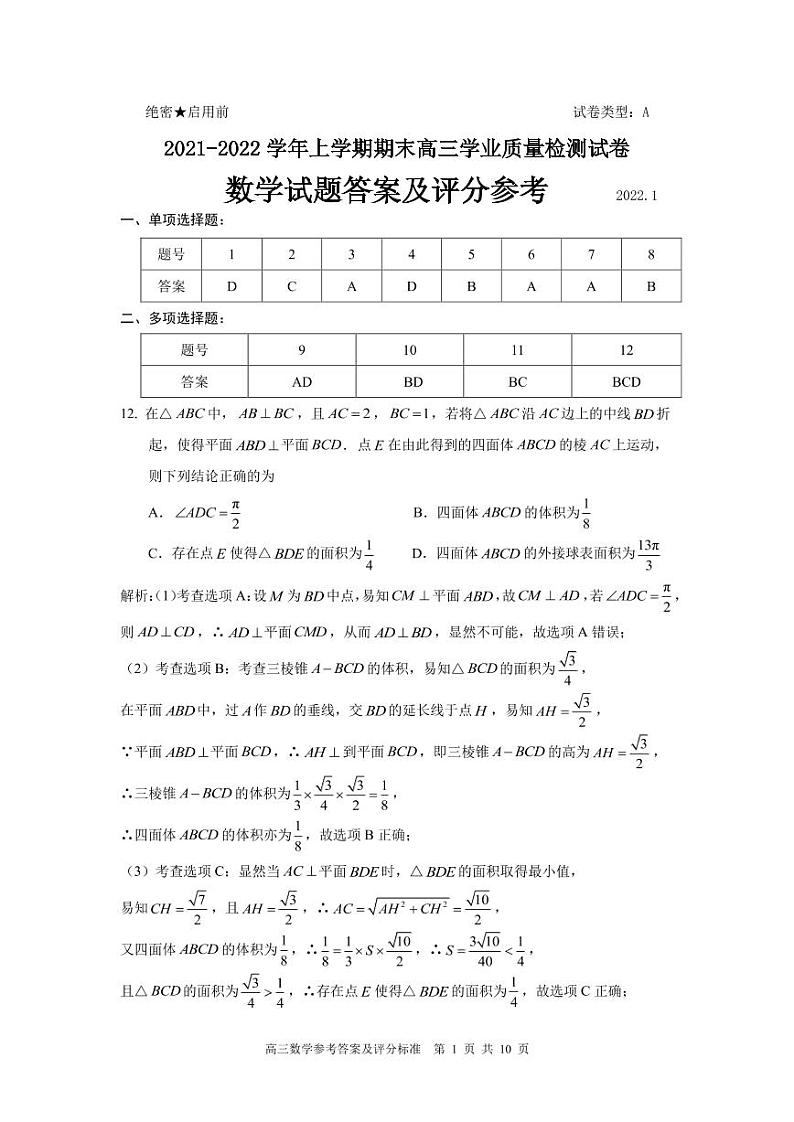
绝密★启用前                                                 试卷类型：A2021-2022学年上学期期末高三学业质量检测试卷      数学试题答案及评分参考     2022.1一、单项选择题： 题号12345678答案DCADBAAB二、多项选择题：题号9101112答案AD BDBCBCD12. 在△中，，且，，若将△沿边上的中线折起，使得平面平面. 点在由此得到的四面体的棱上运动，则下列结论正确的为A． B．四面体的体积为  C．存在点使得△的面积为     D．四面体的外接球表面积为解析：（1）考查选项A：设为中点，易知平面，故，若，则，∴平面，从而，显然不可能，故选项A错误；（2）考查选项B：考查三棱锥的体积，易知△的面积为，在平面中，过作的垂线，交的延长线于点，易知，∵平面平面，∴到平面，即三棱锥的高为，∴三棱锥的体积为，∴四面体的体积亦为，故选项B正确；（3）考查选项C：显然当平面时，△的面积取得最小值，易知，且，∴，又四面体的体积为，∴，∴，且△的面积为，∴存在点使得△的面积为，故选项C正确；（4）考查选项D：设△与△的外心依次为，，过作平面的垂线，过作平面的垂线，则四面体的外接球球心为直线与的交点，易知四边形为矩形，且，，∴四面体的外接球半径， ∴外接球表面积为，故选项D正确；综上所述，应选BCD.三、填空题：13. （或者，均可）；    14. ；     15. ；     16. .16. 已知存在实数，使得不等式成立，则实数的取值范围为          . 解析：∵，显然可取等号，∴的最小值为，∴只需存在实数，使得成立即可，即，易知当时，，∴，∴，∴实数的取值范围为，故应填.三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．（10分）设△的内角，，的对边分别为，，，且．(1)  求角的大小；(2) 若边上的高为，求.解：(1) （解法一）由余弦定理，得，…………………………1分∴， ∴，…………………………………………………………………3分又∵，∴，∴， ………………………………………………………………4分∵为△的内角，∴，∴.  …………………………………………5分（解法二）由正弦定理，得，……………………………………1分∴， ∵，，为△的内角，∴，∴，∴， …………………………………………………………………3分∵，，∴，， ………………………………………4分∴. ………………………………………………………………………………………5分 (2)∵△的面积，∴， …………………………………7分由余弦定理，得，∴， …………………………………………………………………………………9分∴.  ……………………………………………10分或者亦可.   …………………………10分    18．（12分）已知数列满足，，且 ().(1) 证明：数列是等比数列；(2) 记的前项和为，且任意，均有，求实数的最小值.解：(1)∵，∴，…………………………………2分又∵，     …………………………………………………………………………3分∴是以为首项，为公比的等比数列，     …………………………………4分(2)（解法一）由(1)易知，  …………………………………………………5分∴，，…，（），    …………………6分∴（），∴（），  ………………………………………………………………………8分经检验当时，，亦满足，∴()，    ……………………………………………………………………9分∴，      …………………………………………………………10分∵任意，均有，∴()     …………………………………………………11分显然()，∴,即实数的最小值为.    ………………………12分（解法二）由()得，()，…………6分又，∴数列为常数列，即()，………………7分∴()，即数列是以为首项，为公比的等比数列，∴()，    ……………………………………………………………………9分∴，      …………………………………………………………10分∵任意，均有，∴()     …………………………………………………11分显然()，∴,即实数的最小值为.    ………………………12分19．（12分）已知甲、乙、丙三个研究项目的成员人数分别为，，. 现采用分层抽样的方法从中抽取人，进行睡眠时间的调查.(1) 应从甲、乙、丙三个研究项目的成员中分别抽取多少人？(2) 若抽出的人中有人睡眠不足，人睡眠充足，现从这人中随机抽取人做进一步的访谈调研. 若用随机变量表示抽取的人中睡眠充足的成员人数，求的分布列与数学期望.解：(1)由已知，甲、乙、丙三个研究项目的成员人数之比为， ……2分∴应从甲、乙、丙三个研究项目的成员中分别抽取的人数为，，，∴，解得，∴应从甲、乙、丙三个研究项目的成员中分别抽取人，人，人.  …………………4分(2)随机变量的所有可能取值为， …………………………………………………5分则，，，， …………………………9分∴随机变量的分布列为………………………………………………………………………11分随机变量的数学期望.  …………………12分20．（12分）如图，在三棱锥中，△为等腰直角三角形，，△为等边三角形.(1) 证明：；(2) 若直线与平面所成的角为，点在棱上，且，求二面角的大小.    解：(1) 证明：如图，取的中点，连接，，  ………………………………1分∵，∴，  ………………………………………………………………2分∵△为等边三角形，∴，  …………………………3分又∵，平面，∴平面，     ……………………………………4分又∵平面，∴.  …………………………………………………………………5分(2)（解法一）由(1)不难知道，在平面内，若过作直线的垂线，则该垂线亦为平面的垂线，故直线在平面内的射影为直线，∴为直线与平面所成的角，即，……………………………6分不放设，∵，为的中点，∴，∵△为等边三角形，∴，在△中，由正弦定理得，∴，∴，即，由(1)知，，且，…………………………………………………………7分以为坐标原点，，，所在的直线分别为轴，建立如图所示的空间直角坐标系，易得，，，，      则有，，………………………………………………………8分易知为平面的一个法向量，…………………………………………………9分设为平面的一个法向量，则 即∴   则平面的一个法向量为，…10分，…………11分由图可知，二面角为锐角，∴二面角的余弦值为，∴二面角的大小为. ……………12分（解法二）过作，垂足为，过作，垂足为，连接，由(1)不难知道，在平面内，若过作直线的垂线，则该垂线亦为平面的垂线，故直线在平面内的射影为直线，∴为直线与平面所成的角，即，……………………………6分不放设，∵，为的中点，∴，∵△为等边三角形，∴，在△中，由正弦定理得，∴，∴，即.结合(1)可知，二面角为直二面角，…………7分∴平面，又平面，∴,又，平面，∴平面，又平面，∴，∴为二面角的平面角.   ………………………………8分∵，，∴，，， ……………………9分取的中点，连接，则，，∴，…………………………………………………………………10分∴， …………………………………………………………………11分∴二面角的余弦值为，∴二面角的大小为. ……………12分21．（12分）在平面直角坐标系中，点在椭圆上，过点的直线与交于异于点的，两点，记直线，的斜率分别为，，当时，.(1) 求椭圆的方程； (2) 证明：为定值.解：(1) ∵在上，∴，………………………………………………………1分当时，直线的方程为：，将代入，并整理得，解得，或，………………2分∴，解得，∴椭圆的方程为：.  ………………………………………………………4分 (2)由题意知，直线的斜率存在，不妨设直线的方程为，，，  ………………………5分联立得， ………………………7分∴，且， …………………………………………………8分∴， ……………11分∴，即为定值. ………………………………………………………12分22．（12分）已知定义在上的函数().(1) 求的单调递增区间；(2) ，若不等式恒成立，求实数的取值范围. 解：(1) ，   ………………………………………………………………1分①当时，，∴在上单调递减，即无单调递增区间；………………………………………2分②当时，令，则，∴在上单调递增， ……………………………………………………………………3分令，解得，∴当时，；当时，，………………4分∴在上单调递减；在上单调递增，∴的单调递增区间为，综上所述，当时，的单调递增区间为；当时，无单调递增区间.     ……………………………………………………………………………………5分(2)由(1)可知，当时，有最小值，且最小值为， 即，，当且仅当时等号成立，  ………………………………………6分易知不等式等价于，∴当时，须有成立， ………………………………………………………7分令，则，∴在上单调递增，又，∴等价于，    …………………………………………………………………8分下证当时，，有不等式恒成立.（证法一）一方面，∵，，∴，，即， …………………………………………9分∴，，∴，， ……………………………………………………10分∴只需证当时，，有不等式恒成立即可，另一方面，由，，可得，∴，又当时，，显然有， …………………………………………11分∴当时，，显然有不等式恒成立，∴当时，，显然不等式恒成立，综上所述，实数的取值范围为.    ………………………………………………12分（证法二）令，，则，∴为单调递增函数，∴的最小值为， ………………………………………………9分下证，∵，，∴只需证，∴只需证，即证，…………………………………………10分令，则，易知的最小值为，∴，即，∴当时，，显然有不等式恒成立，∴当时，，显然不等式恒成立，综上所述，实数的取值范围为.    ………………………………………………12分