




- 17.1.2勾股定理的应用课件PPT 课件 5 次下载
- 17.1.3勾股定理的作图与计算课件PPT 课件 4 次下载
- 17.2.2勾股定理及其逆定理的综合运用课件PPT 课件 3 次下载
- 第17章勾股定理的单元复习课件PPT 课件 0 次下载
- 18.1.1平行四边形的性质(1)课件PPT 课件 3 次下载
数学八年级下册第十七章 勾股定理17.2 勾股定理的逆定理教案配套ppt课件
展开理解勾股定理的逆定理,经历“实验——猜想——论证”的探究过程,体会构造法证明数学命题的基本思想方法。
理解原命题、逆命题、逆定理的概念及关系。
设直角三角形的两条直角边长分别为a和b,斜边长为c。(1)已知a=3,b =4, 求c(2)已知a=3,c =4, 求b
古埃及人把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角变式直角。
这个问题意味着,如果围城的三角形的三边长分别为3,4,5,它们满足关系“32+42=52”,那么围成的三角形是直角三角形。你认为正确吗?
2.动手画一画分别以下面两组数画三角形(单位是厘米):a=2.5,b=6, c=6.5;a=4,b=7.5, c=8.5。
这两组数都满足a2+b2=c2 它们都是直角三角形。
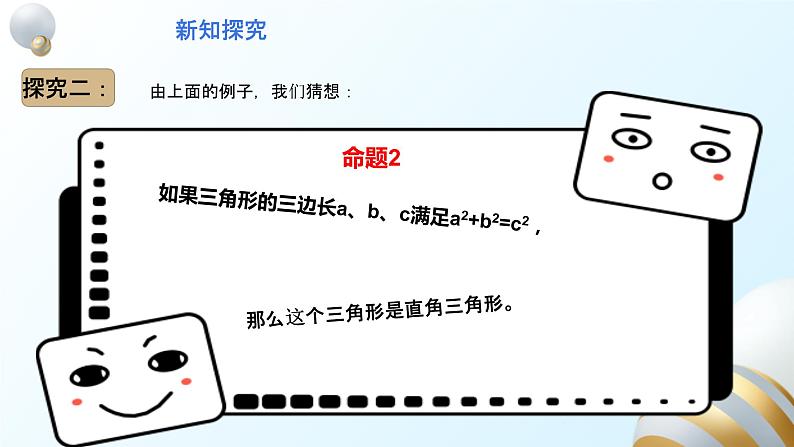
由上面的例子,我们猜想:
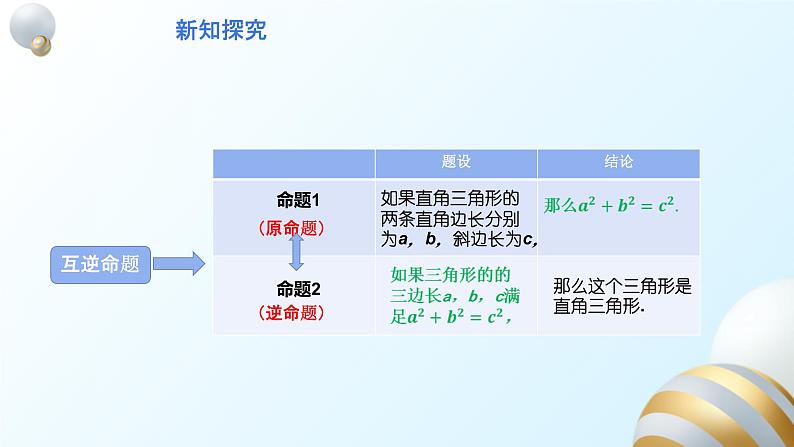
如果三角形的三边长a、b、c满足a2+b2=c2,
那么这个三角形是直角三角形。
如果直角三角形的两条直角边长分别为a,b,斜边长为c,
那么这个三角形是直角三角形.
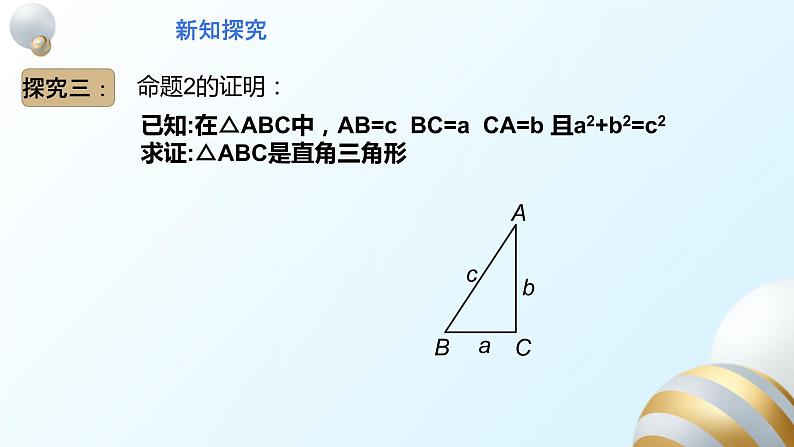
已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ABC是直角三角形
证明:画一个△A′B′C′,使∠ C′=900,B′C′=a, C′A′=b
由勾股定理可得 a2+b2=A′B′2
在△ ABC和△ A′B′C′中
BC=a=B′C′CA=b=C′A′AB=c=A′B′
∴ △ ABC ≌△ A′B′C′(SSS)
∴ ∠ C= ∠ C′=900
∴ △ ABC是直角三角形
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2
勾股定理的逆定理 如果三角形的三边长a、b、c满足那么这个三角形是直角三角形.
a2 + b2 = c2
能够成为直角三角形三条边长的三个正整数,称为勾股数 .
(1)a=15 , b =8 , c=17;
例1 判断由线段a、b、c组成的三角形是不是直角三角形:
根据勾股定理的逆定理,一个三角形中两条较小边长的平方和等于最大边长的平方,那么这个三角形是直角三角形.
(2)a=13 , b =14 , c=15;
解:(1)∵a2+b2=152+82=225+64=289 c2=172=289 ∵a2+b2=c2 ∴根据勾股定理的逆定理, 这个三角形是直角三角形。
(2) ∵ 132+142=169+196=365 152=225, ∴132+142≠152 ∴根据勾股定理的逆定理,这个三角形不是直角三角形.
两条较小边长的平方和=最大边长的平方
(1)a=15 , b =8 , c=17;
例1: 判断由线段a、b、c组成的三角形是不是直角三角形:
步骤: ①排序; ②计算; ③判断.
例2:下列定理中,哪些有逆定理?如果有逆定理,请写出逆定理。(1)同旁内角互补,两直线平行,(2)三边对应相等的两个三角形全等。
解:(1)逆定理:两直线平行,同旁内角互补。 (2)逆定理:如果两个三角形全等,那么这两个三角形的三边对应相等。
①排序; ②计算; ③判断.
勾股定理的逆定理(判定直角三角形的依据)
∵△ABC是直角三角形∴a2+b2=c2
∵在△ABC是a2+b2=c2△ABC是直角三角形
初中人教版17.2 勾股定理的逆定理一等奖教学课件ppt: 这是一份初中人教版<a href="/sx/tb_c10262_t3/?tag_id=26" target="_blank">17.2 勾股定理的逆定理一等奖教学课件ppt</a>,文件包含人教版数学八年级下册1721《勾股定理的逆定理》课件pptx、人教版数学八年级下册1721《勾股定理的逆定理》教学设计docx、人教版数学八年级下册1721《勾股定理的逆定理》导学案docx等3份课件配套教学资源,其中PPT共33页, 欢迎下载使用。
初中数学人教版八年级下册17.2 勾股定理的逆定理背景图课件ppt: 这是一份初中数学人教版八年级下册17.2 勾股定理的逆定理背景图课件ppt,文件包含第1课时勾股定理的逆定理pptx、互逆命题mp4、勾股定理逆定理导入mp4等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
人教版八年级下册17.2 勾股定理的逆定理教案配套课件ppt: 这是一份人教版八年级下册17.2 勾股定理的逆定理教案配套课件ppt,共26页。PPT课件主要包含了课堂导入,结论能成立吗,探究新知,画一画,证一证,最长边,判断等量关系,典例分析,练一练,知识点2勾股数等内容,欢迎下载使用。














