初中数学人教版八年级下册18.1.1 平行四边形的性质评课课件ppt

这是一份初中数学人教版八年级下册18.1.1 平行四边形的性质评课课件ppt，共20页。PPT课件主要包含了教学目标，验证猜想等内容，欢迎下载使用。
理解并掌握平行四边形的概念及性质：对边相等、对角相等。
会用平行四边形的性质进行简单的计算及有关论证。
培养学生发现问题、解决问题的能力及逻辑推理能力．
观察下列图片，是我们生活中常见的什么图形？
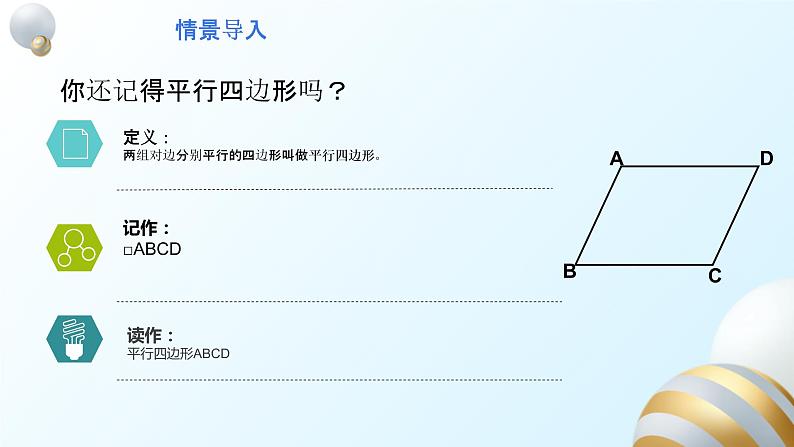
你还记得平行四边形吗？
定义：两组对边分别平行的四边形叫做平行四边形。
读作：平行四边形ABCD
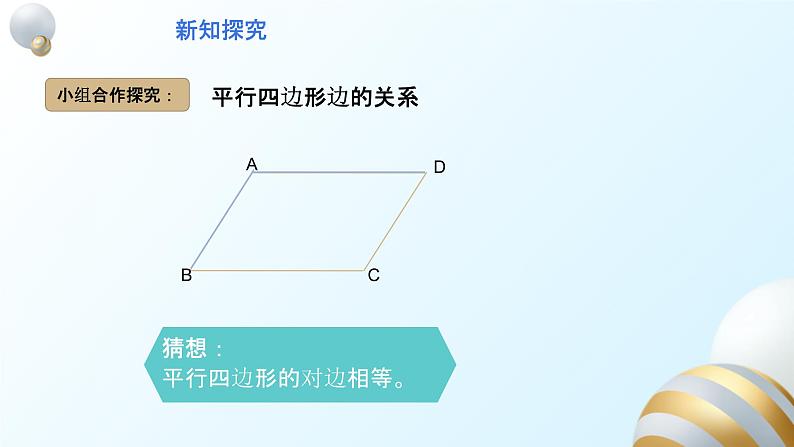
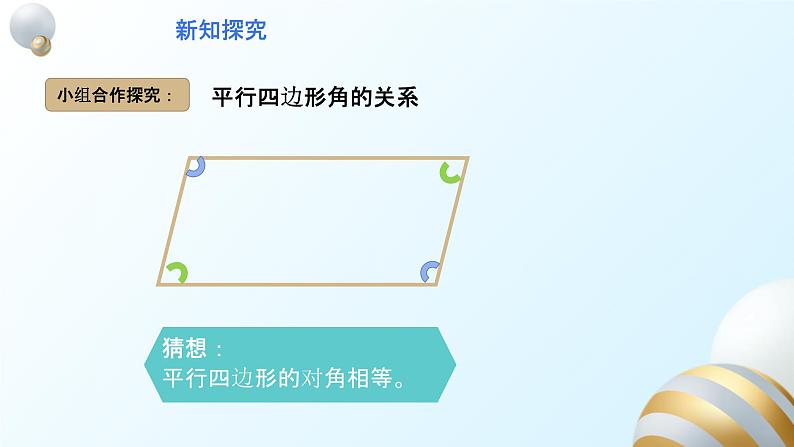
根据定义画一个平行四边形，观察它，除了“两组对边分别平行”外，它的边之间还有什么关系？它的角之间有什么关系？度量一下，和你的猜想一样吗？
平行四边形的对边相等。
平行四边形的对角相等。
已知：四边形ABCD是平行四边形.求证：AB=CD,AD=BC ，∠A=∠C,∠B=∠D.
∵AD∥BC,AB∥CD
∴∠1=∠2，∠3=∠4
又∵AC是△ABC和△CDA的公共边
∴AD=CB，AB=CD
已知： ABCD求证：AB=CD，AD=BC；∠B=∠D，∠BAD=∠DCB
即∠BAD＝∠DCB.
证明：连接AC. ∵四边形ABCD为平行四边形，
∴AB∥CD，AD∥BC.
∴∠1＝∠2，∠3＝∠4
∵∠1＝∠2，AC＝CA，∠4＝∠3
∴ △ABC≌△CDA（ASA）
∴AB＝CD，BC＝DA，∠B＝∠D
又∵∠1＝∠2，∠3＝∠4
∴∠1＋∠3＝∠2＋∠4
平行四边形的性质：1.平行四边形对边相等。2.平行四边形对角相等。
例1： 如图，在□ ABCD中，DE⊥AB，BF⊥CD，垂足分别为E、F.求证：AE=CF.
证明：∵四边形ABCD是平行四边形，
∴∠A=∠C，AD=CB.
又∠AED=∠CFB=90°,
∴△ADE≌△CBF.
例2：如图，四边形ABCD是平行四边形，E，F是对角线AC的三等分点，连接BE，DF．证明BE=DF．
∴AB=CD，AB∥CD，
∴∠BAE=∠DCF，
∵E，F是对角线AC的三等分点，
在△ABE和△CDF中，
∴△ABE≌△CDF（SAS），
例3：如图，A，B两点被大山阻隔，为了改善山区的交通，现拟开凿一个贯穿A，B的隧道，修建一条高速公路．请你设计出一个方案，利用平移的有关知识测量出A，B之间的距离和隧道开凿的方向．
解：可以设法将线段“平移”出来，便于测量．如图，分别沿A，B两点向同一个方向行走相同距离得到点，测量线段即可，这是其中一种方法．
平行四边形的对边平行且相等.
平行四边形的对角相等.
定义：有两组对边分别平行的四边形是平行四边形.
1 在四边形ABCD中，∠A=∠C，∠1=∠2，求证：四边形ABCD是平行四边形．
证明：∵∠1=∠2, ∴AD∥BC.
∵AD∥BC,∴四边形ABCD是平行四边形.
2.如图, 在□ABCD中，E，F分别是AB，CD的中点.求证：四边形EBFD是平行四边形.
证明：∵四边形ABCD是平行四边形, ∴AB=CD，EB∥FD.
又∵EB∥FD，∴四边形EBFD是平行四边形.
3.如图, □ABCD的对角线AC，BD相交于点O，E，F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形, ∴OA=OC，OB=OD.
∵AE=CF,∴OA-AE=OC-CF，即OE=OF.
又∵OB=OD,∴四边形BFDE是平行四边形.
4.如图: □ ABCD的对角线AC，BD相交于点O，E，F分别是OA，OC的中点，求证：BE=DF．
证明：连接DE，BF.
∵四边形ABCD是平行四边形,∴OD=OB，OA=OC.
∵E，F分别是OA，OC的中点,
∴OE=OF,又∵OD=OB∴四边形DEBF是平行四边形,∴BE=DF.
5.如图,E,F是▱ABCD的对角线AC上的两点,AE＝CF.求证:(1)△ADF≌△CBE;(2)EB∥DF.
证明:(1)∵AE＝CF,∴AE＋EF＝CF＋EF,即AF＝CE.∵四边形ABCD是平行四边形,∴AD＝CB,AD∥CB.∴∠DAF＝∠BCE.∴△ADF≌△CBE(SAS).(2)∵△ADF≌△CBE,∴∠DFA＝∠BEC.∴EB∥DF.