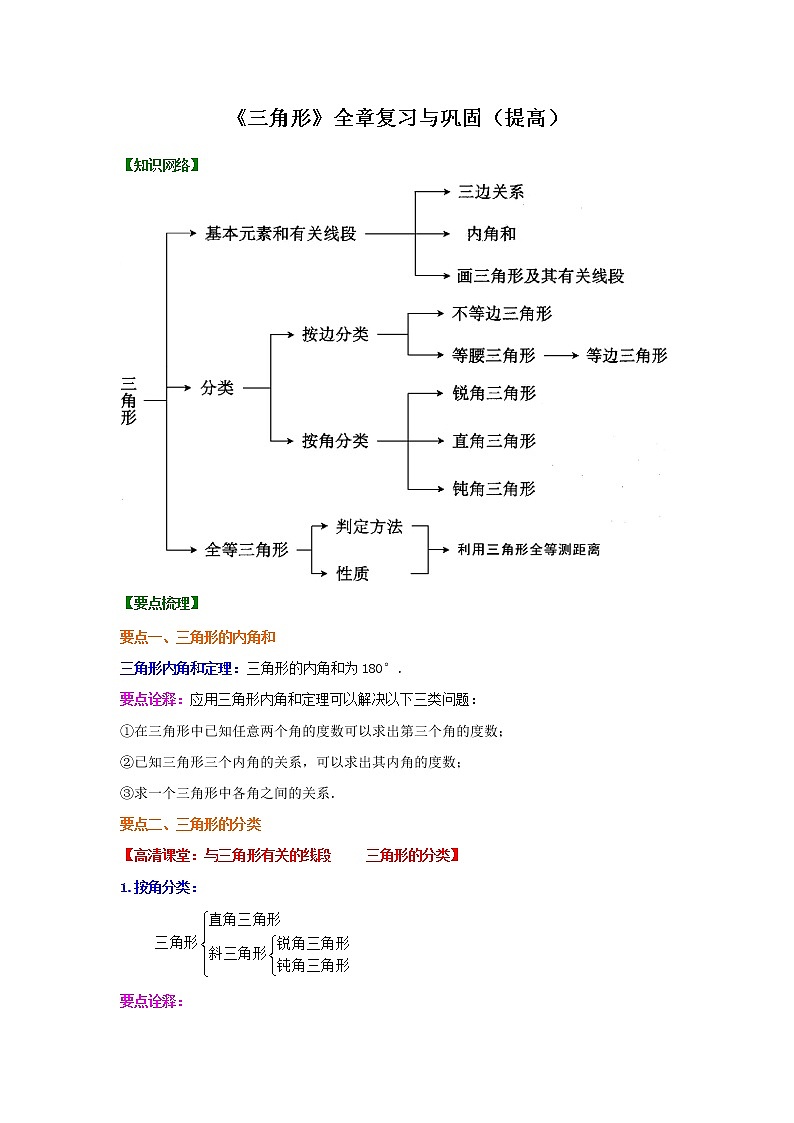
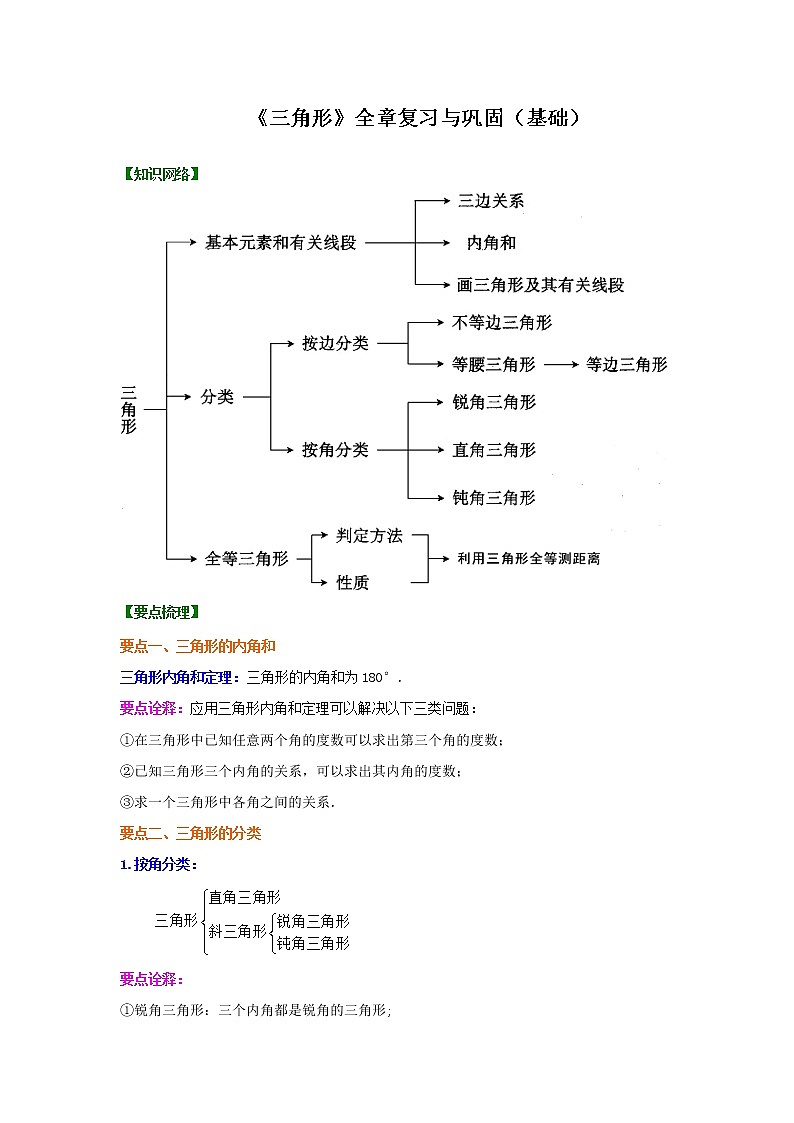
初中北师大版第四章 三角形综合与测试课时作业

这是一份初中北师大版第四章 三角形综合与测试课时作业，文件包含《三角形》全章复习与巩固提高巩固练习docx、《三角形》全章复习与巩固提高知识讲解doc、《三角形》全章复习与巩固基础巩固练习docx、《三角形》全章复习与巩固基础知识讲解doc等4份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。

1．下列图形中具有稳定性的是（ ）
A．正三角形B．正方形C．正五边形D．正六边形
2.已知三角形两边长分别为4 cm和9 cm，则下列长度的四条线段中能作为第三边的是 ( )
A．13 cm B．6 cm C．5 cm D．4 cm
3.下列说法不正确的是（ ）
A．三角形的中线在三角形的内部
B．三角形的角平分线在三角形的内部
C．三角形的高在三角形的内部
D．三角形必有一高线在三角形的内部
4. 在下列结论中, 正确的是( )
A.全等三角形的高相等B.顶角相等的两个等腰三角形全等
C. 一角对应相等的两个直角三角形全等D.一边对应相等的两个等边三角形全等
5. 图中的尺规作图是作（ ）
A. 线段的垂直平分线 B. 一条线段等于已知线段
C. 一个角等于已知角 D. 角的平分线
6．如图，AC=AD，BC=BD，则有（ ）
A. AB垂直平分CD B. CD垂直平分AB
C. AB与CD互相垂直平分 D. CD平分∠ACB
7. 如图，△ABC中∠ACB＝90°,CD是AB边上的高，∠BAC的角平分线AF交CD于E，则△CEF必为（ ）
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
8. 若△ABC的∠A＝60°，且∠B:∠C＝2:1，那么∠B的度数为 ( )
A．40° B．80° C．60° D．120°
二.填空题
9.如图，在▱ABCD中，E、F为对角线AC上两点，且BE∥DF，请从图中找出一对全等三角形： ．
10. △ABC和△ADC中，下列三个论断：①AB＝AD；②∠BAC＝∠DAC；③BC＝DC．将两个论断作为条件，另一个论断作为结论构成一个命题，写出一个真命题：__________．
11. 如图，在△ABC中， ED垂直平分BC，EB=3．则CE长为 ．
12. 若三角形三个外角的度数比为2∶3∶4，则此三角形内角分别为____ ____．
13. 如右图，在△ABC中，∠C＝90°，BD平分∠CBA交AC于点D．若AB＝，CD＝，则△ADB的面积为______________ ．
14．在△ABC中，∠B=60°，∠C=40°，AD、AE分别是△ABC的高线和角平分线， 则∠DAE的度数为_________.
15. 如图，△ABC中，H是高AD、BE的交点，且BH＝AC，则∠ABC＝________.
16. 如图，△ABC中，BO、CO分别平分∠ABC、∠ACB，OM∥AB，ON∥AC，BC＝10，则ΔOMN的周长＝______．
三.解答题
17.如图，∠1=∠2，∠3=∠4，求证：AC=AD．
18．作图题（不写作图步骤，保留作图痕迹）．
已知：在下面的△ABC中，用尺规作出AB边上的高（不写作法，保留作图痕迹）
19.有一座小山，现要在小山A、B的两端开一条隧道，施工队要知道A、B两端的距离，于是先在平地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD=CA，连接BC并延长到E，使CE=CB，连接DE，那么量出DE的长，就是A、B的距离，你能说说其中的道理吗？
20．已知：如图，中，，AD⊥BC于D，CF交AD于点F，连接BF
并延长交AC于点E，．
求证：（1）△ABD≌△CFD；（2）BE⊥AC．
【答案与解析】
一.选择题
1. 【答案】A
2. 【答案】B；
【解析】根据三角形的三边关系进行判定．
3. 【答案】C；
【解析】解：A、三角形的中线在三角形的内部正确，故本选项错误；
B、三角形的角平分线在三角形的内部正确，故本选项错误；
C、只有锐角三角形的三条高在三角形的内部，故本选项正确；
D、三角形必有一高线在三角形的内部正确，故本选项错误．
故选C．
4. 【答案】D；
【解析】A项应为全等三角形对应边上的高相等；B项如果腰不相等不能证明全等；C项直角三角形至少要有一边相等.
5. 【答案】A；
【解析】根据图象是一条线段，它是以线段的两端点为圆心，作弧，进而作出垂直平分线，故做的是：线段的垂直平分线.
6. 【答案】A；
【解析】∵AC=AD，BC=BD，
∴点A，B在线段CD的垂直平分线上．
∴AB垂直平分CD．
故选A．
7. 【答案】A；
【解析】∠CFA＝∠B＋∠BAF，∠CEF＝∠ECA＋∠EAC，而∠B＝∠ECA，∠BAF＝∠EAC，故△CEF为等腰三角形.
8. 【答案】B；
【解析】根据三角形内角和180°，以及已知条件可以计算得出∠B的度数为120°.
二.填空题
9.【答案】△ADF≌△BEC．
【解析】∵四边形ABCD是平行四边形，
∴AD=BC，∠DAC=∠BCA，
∵BE∥DF，
∴∠DFC=∠BEA，
∴∠AFD=∠BEC，
在△ADF与△CEB中，
，
∴△ADF≌△BEC（AAS）.
10．【答案】①②③；
11. 【答案】3；
【解析】∵ED垂直平分BC，
∴可得△BED≌△CED（SAS）
∴CE=BE=3.
12. 【答案】100°，60°，20°．
13.【答案】；
【解析】由三角形全等知D点到AB的距离等于CD＝，所以△ADB的面积为.
14. 【答案】10°．
15.【答案】45°；
【解析】Rt△BDH≌Rt△ADC，BD＝AD.
16. 【答案】10；
【解析】OM＝BM，ON＝CN，∴△OMN的周长等于BC.
三.解答题
17.【解析】
证明：∵∠3=∠4，
∴∠ABC=∠ABD，
在△ABC和△ABD中，，
∴△ABC≌△ABD（ASA），
∴AC=AD．

18.【解析】
解：
19.【解析】
解：在△ABC和△CED中，
AC=CD，∠ACB=∠ECD（对顶角），EC=BC，
∴△ABC≌△DEC，
∴AB=ED，
即量出DE的长，就是A、B的距离.
20．【解析】
证明：(1) ∵ AD⊥BC，∴ ∠ADC＝∠FDB＝90°.
∵ ，
∴
∴ AD＝CD
∵ ，
∴ △ABD≌△CFD
(2)∵△ABD≌△CFD
∴ BD＝FD.
∵ ∠FDB＝90°，
∴ .
∵ ，
∴ .
∴ BE⊥AC．