初中数学人教版九年级下册28.1 锐角三角函数学案

这是一份初中数学人教版九年级下册28.1 锐角三角函数学案，文件包含人教版九年级数学下册同步精品第10讲锐角三角函数教师版doc、人教版九年级数学下册同步精品第10讲锐角三角函数学生版doc等2份学案配套教学资源，其中学案共24页， 欢迎下载使用。
第10讲  锐角三角函数 课程标准1．结合图形理解记忆锐角三角函数定义；
2．会推算30°、45°、60°角的三角函数值，并熟练准确的记住特殊角的三角函数值；
3．理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.  知识点01  锐角三角函数的概念如图所示，在Rt△ABC中，∠C＝90°，∠A所对的边BC记为a，叫做∠A的对边，也叫做∠B的邻边，∠B所对的边AC记为b，叫做∠B的对边，也是∠A的邻边，直角C所对的边AB记为c，叫做斜边．
　     锐角A的对边与斜边的比叫做∠A的正弦，记作sinA，即；锐角A的邻边与斜边的比叫做∠A的余弦，记作cosA，即；锐角A的对边与邻边的比叫做∠A的正切，记作tanA，即.同理；；．
要点诠释：
　　(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化．
　　(2)sinA，cosA，tanA分别是一个完整的数学符号，是一个整体，不能写成，，
　 　　，不能理解成sin与∠A，cos与∠A，tan与∠A的乘积．书写时习惯上省略∠A的角的记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成
　 　　“tanAEF”；另外，、、常写成、、．
　　(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．
　　(4)由锐角三角函数的定义知：当角度在0°<∠A<90°间变化时，，，tanA＞0． 知识点02  特殊角的三角函数值　　　利用三角函数的定义，可求出30°、45°、60°角的各三角函数值，归纳如下：锐角30°45°160°要点诠释：
　　(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．
　　(2)仔细研究表中数值的规律会发现：
　 　　、、的值依次为、、，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：
　 　　①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)；
　 　　②余弦值随锐角度数的增大(或减小)而减小(或增大)．
 知识点03  锐角三角函数之间的关系 　　如图所示，在Rt△ABC中，∠C=90°．
　　(1)互余关系：，；
　　(2)平方关系：；
　　(3)倒数关系：或；
　　(4)商数关系：．
　　要点诠释：
　　锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．
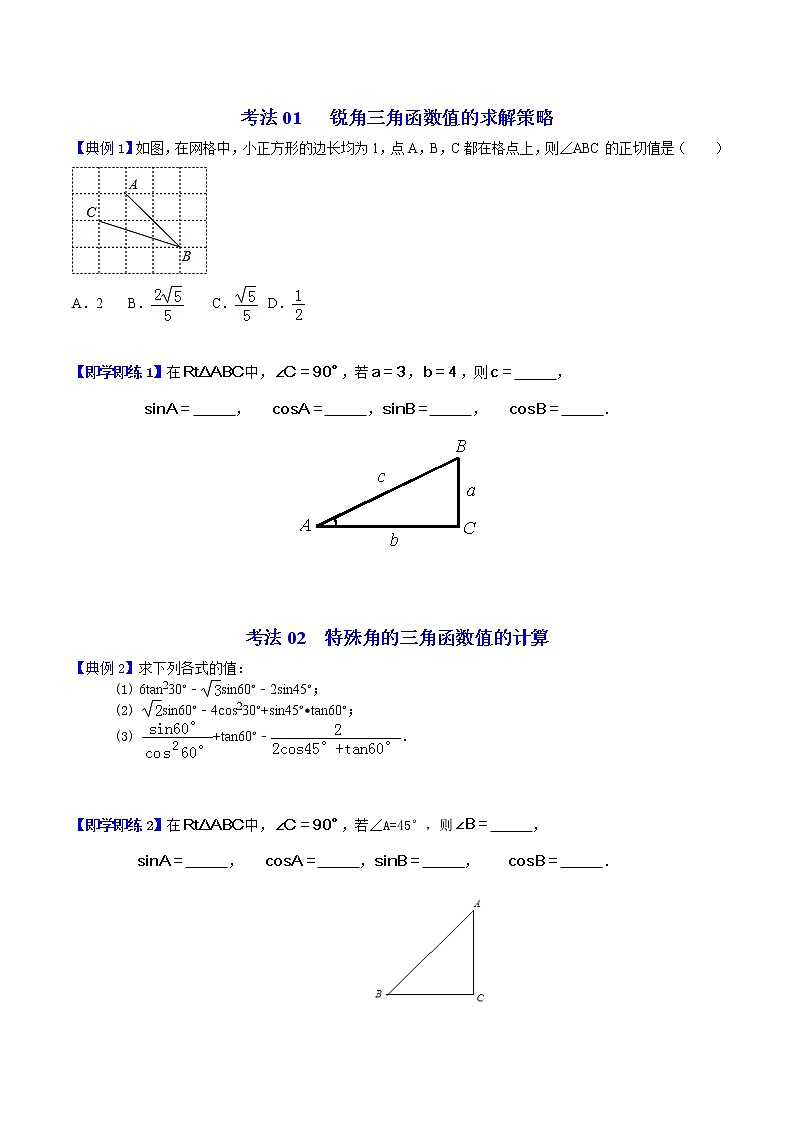
  考法01   锐角三角函数值的求解策略【典例1】如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是（　　）A．2 B． C． D．【思路点拨】根据勾股定理，可得AC、AB的长，根据正切函数的定义，可得答案．【答案】D．【解析】解：如图：，由勾股定理，得AC=，AB=2，BC=，∴△ABC为直角三角形，∴tan∠B==，故选：D．【总结升华】本题考查了锐角三角函数的定义，先求出AC、AB的长，再求正切函数． 【即学即练1】在中，，若，，则      ，            ，         ，      ，         ．    【答案】 5 ， ， ，， ． 考法02  特殊角的三角函数值的计算【典例2】求下列各式的值： (1) 6tan230°﹣sin60°﹣2sin45°； (2) sin60°﹣4cos230°+sin45°•tan60°； (3) +tan60°﹣． 【答案与解析】解：（1）原式==．    (2) 原式=×﹣4×（）2+×=﹣3+=；    (3) 原式=+﹣=2+﹣=3﹣2+2=．【总结升华】熟记特殊角的三角函数值或借助两个三角板推算三角函数值，先代入特殊角的三角函数值，再进行化简． 【即学即练2】在中，，若∠A=45°，则      ，           ，         ，      ，          ．【答案】45°，， ，， ．考法03  锐角三角函数之间的关系【典例3】已知△ABC中的∠A与∠B满足（1﹣tanA）2+|sinB﹣|=0（1）试判断△ABC的形状．（2）求（1+sinA）2﹣2﹣（3+tanC）0的值．【答案与解析】解：（1）∵|1﹣tanA）2+|sinB﹣|=0，∴tanA=1，sinB=，∴∠A=45°，∠B=60°，∠C=180°﹣45°﹣60°=75°，∴△ABC是锐角三角形；（2）∵∠A=45°，∠B=60°，∠C=180°﹣45°﹣60°=75°，∴原式=（1+）2﹣2﹣1=．【总结升华】本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键． 考法04  锐角三角函数的拓展探究与应用【典例4】如图所示，AB是⊙O的直径，且AB＝10，CD是⊙O的弦，AD与BC相交于点P，若弦CD＝6，试求cos∠APC的值．              【答案与解析】连结AC，∵  AB是⊙O的直径，∴  ∠ACP＝90°，又∵ ∠B＝∠D，∠PAB＝∠PCD，∴  △PCD∽△PAB，∴  ． 又∵  CD＝6，AB＝10，∴  在Rt△PAC中， ． 【总结升华】直角三角形中，锐角的三角函数等于两边的比值，当这个比值无法直接求解，可结合相似三角形的性质，利用对应线段成比例转换，间接地求出这个比值．锐角的三角函数是针对直角三角形而言的，故可连结AC，由AB是⊙O的直径得∠ACB＝90°，，PC、PA均为未知，而已知CD＝6，AB＝10，可考虑利用△PCD∽△PAB得． 【典例5】通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对(sad)．如图1①，在△ABC中，AB＝AC，顶角A的正对记作sadA，这时．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：(1)sad60°＝________．(2)对于0＜A＜180°，∠A的正对值sadA的取值范围是_______．(3)如图1②，已知sinA＝，其中∠A为锐角，试求sadA的值．  【答案与解析】(1)1；  (2)0＜sadA＜2；(3)如图2所示，延长AC到D，使AD＝AB，连接BD．设AD＝AB＝5a，由得BC＝3a，∴  ，∴  CD＝5a-4a＝a，，∴  ．【总结升华】(1)将60°角放在等腰三角形中，底边和腰相等，故sadA＝1；(2)在图①中设想AB＝AC的长固定，并固定AB让AC绕点A旋转，当∠A接近0°时，BC接近0，则sadA接近0但永远不会等于0，故sadA＞0，当∠A接近180°时，BC接近2AB，则sadA接近2但小于2，故sadA＜2；(3)将∠A放到等腰三角形中，如图2所示，根据定义可求解． 题组A  基础过关练1. 如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，则下列结论不正确的是（　　）A． B． C． D．【答案】C.【解析】在Rt△ABC中，∠BAC=90°，sinB=，∵AD⊥BC，∴sinB=，sinB=sin∠DAC=，综上，只有C不正确故选：C．2.如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是（　　）　 A．2 B．  C．  D． 【答案】D；【解析】如图：由勾股定理得，AC=，AB=2，BC=，∴△ABC为直角三角形，∴tan∠B==，故选：D． 3. 已知锐角α满足sin25°＝cosα，则α＝(    )A．25°     B．55°     C．65°      D．75°【答案】C；【解析】由互余角的三角函数关系，，∴ sin25°-sin(90°-α)，即90°-α＝25°，∴ α＝65°． 4．如图所示，直径为10的⊙A经过点C(0，5)和点O(0，0)，B是y轴右侧⊙A优弧上一点，则∠OBC的余弦值为  (    )A．       B．       C．      D．【答案】C；【解析】设⊙A交x轴于另一点D，连接CD，根据已知可以得到OC＝5，CD＝10，∴  ，∵  ∠OBC＝∠ODC，∴  ． 5．如图，在△ABC中，∠A＝120°，AB＝4，AC＝2，则sinB的值是(    )A．       B．      C．      D．【答案】D；【解析】如图所示，过点C作CD⊥AB于D，∵  ∠BAC＝120°，∴  ∠CAD＝60°，          又∵  AC＝2，∴  AD＝1，CD＝，          ∴  BD＝BA+AD＝5，在Rt△BCD中，，          ∴  ．              6．在Rt△ABC中，∠C＝90°，若将各边长度都扩大为原来的2倍，则∠A的正弦值(   )A．扩大2倍     B．缩小2倍     C．扩大4倍     D．不变【答案】D；【解析】根据锐角三角函数的定义，锐角三角函数值等于相应边的比，与边的长度无关，而只与边的比值或角的大小有关． 7．如图所示是教学用具直角三角板，边AC＝30cm，∠C＝90°，tan∠BAC＝，则边BC的长为(    )A．cm      B．cm      C．cm      D．cm【答案】C；【解析】由，∴     8. 如图所示，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，若AC＝，BC＝2，则sin∠ACD的值为(    )A．         B．       C．       D． 【答案】A；   【解析】 ∵  ，∴   题组B  能力提升练9．如图，点A（3，t）在第一象限，OA与x轴所夹的锐角为α，tanα=，则t的值是　   　．【答案】．【解析】过点A作AB⊥x轴于B，∵点A（3，t）在第一象限，∴AB=t，OB=3，又∵tanα===，∴t=．故答案为：． 10. 用不等号连接下面的式子．(1)cos50°________cos20°     (2)tan18°________tan21°【答案】(1)＜；   (2)＜；【解析】当α为锐角时，其余弦值随角度的增大而减小，∴  cos50°＜cos20°；当α为锐角时，其正切值随角度的增大而增大，∴  tan18°＜tan21°． 11．在△ABC中，若，∠A、∠B都是锐角，则∠C的度数为       .【答案】105°；【解析】∵  ，           ∴  ，           即，．           又∵ ∠A、∠B均为锐角，∴ ∠A＝45°，∠B＝30°，         在△ABC中，∠A+∠B+∠C＝180°，∴ ∠C＝105°． 12．如图所示，△ABC的顶点都在方格纸的格点上，则sinA＝________．【答案】；   【解析】假设每一个小正方形的边长为1，利用网格，从C点向AB所在直线作垂线CH．垂足为H，则∠A在直角△ACH中，利用勾股定理得，∴  ． 13．已知：正方形ABCD的边长为2，点P是直线CD上一点，若DP＝1，则tan∠BPC的值是________．                    第12题                           第15题 【答案】2或【解析】此题为无图题，应根据题意画出图形，如图所示，由于点P是直线CD上一点，所以点P既可以在边CD上，也可以在CD的延长线上，当P在边CD上时，；当P在CD延长线上时，．         14．如果方程的两个根分别是Rt△ABC的两条边，△ABC的最小角为A，那么tanA的值为________．【答案】或；   【解析】由得，，①当3为直角边时，最小角A的正切值为；②当3为斜边时，另一直角边为，∴  最小角A的正切值为.故应填或．15．如图所示，△ABC的内心在y轴上，点C的坐标为(2，0)，点B的坐标是(0，2)，直线AC的解析式为，则tanA的值是________．【答案】；【解析】由△ABC的内心在y轴上可知OB是∠ABC的角平分线，则∠OBA＝45°，易求AB与x轴的交点为(-2，0)，所以直线AB的解析式为：，联立可求A点的坐标为(-6，-4)，∴ ，又OC＝OB＝2，∴  BC＝．在Rt△ABC中，．16.若α为锐角，且，则m的取值范围是             　．【答案】 ；  【解析】∵0＜cosα＜1，∴0＜＜1，解得.  题组C  培优拔尖练17．如图所示，△ABC中，D为AB的中点，DC⊥AC，且∠BCD＝30°，求∠CDA的正弦值、余弦值和正切值．【答案与解析】    过D作DE∥AC，交BC于点E．    ∵  AD＝BD，∴  CE＝EB，∴  AC＝2DE．    又∵ DC⊥ AC，DE∥AC，    ∴  DC⊥DE，即∠CDE＝90°．    又∵  ∠BCD＝30°，∴  EC＝2DE，DC＝DE．    设DE＝k，则CD＝，AC＝2k．在Rt△ACD中，．∴  ，．．             18. 计算下列各式的值．   (1) ；(2) sin45°+tan45°﹣2cos60°．(3) ﹣cos60°．【答案与解析】解：（1）原式=4×﹣×+×=1+3．      (2) 原式=×+1﹣2×=1+1﹣1=1．(3) 原式=﹣×=﹣=． 19．如图所示，在矩形ABCD中，E是BC边上的点，AE＝BC，DF⊥AE，垂足为F，连接DE． (1)求证：AB＝DF；(2)若AD＝10，AB＝6，求tan∠EDF的值．【答案与解析】    (1)证明：∵  四边形ABCD是矩形，∴  AD∥BC，AD＝BC∴  ∠DAF＝∠AEB又∵  AE＝BC，∴  AE＝AD又∵  ∠B=∠DFA＝90°，∴  △EAB≌△ADF．∴  AB＝DF．(2)解：在Rt△ABE中，       ∵  △EAB≌△ADF，∴  DF＝AB＝6，AF＝EB＝8，∴  EF＝AE-AF＝10-8＝2．∴  ．20. 如图所示，已知⊙O的半径为2，弦BC的长为，点A为弦BC所对优弧上任意一点(B、C两点除外)．(1)求∠BAC的度数；(2)求△ABC面积的最大值．(参考数据：，，．                                                                        【答案与解析】(1)连接BO并延长，交⊙O于点D，连接CD．∵  BD是直径，∴  BD＝4，∠DCB＝90°．在Rt△DBC中，，∴  ∠BDC＝60°，∴  ∠BAC＝∠BDC＝60°．         (2)因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A应落在优弧BC的中点处．过O作OE⊥BC于点E，延长EO交⊙O于点A，则A为优孤BC的中点．连结AB，AC，则AB＝AC，∠BAE∠BAC＝30°．在Rt△ABE中，∵  BE，∠BAE＝30°，∴  ，∴  ．答：△ABC面积的最大值是．