华师大版八年级上册第13章 全等三角形13.3 等腰三角形2 等腰三角形的判定课堂教学ppt课件

这是一份华师大版八年级上册第13章 全等三角形13.3 等腰三角形2 等腰三角形的判定课堂教学ppt课件，共20页。PPT课件主要包含了它是真命题吗，巩固练习，ABAC，思考题，等边三角形的判定定理，课堂小结等内容，欢迎下载使用。

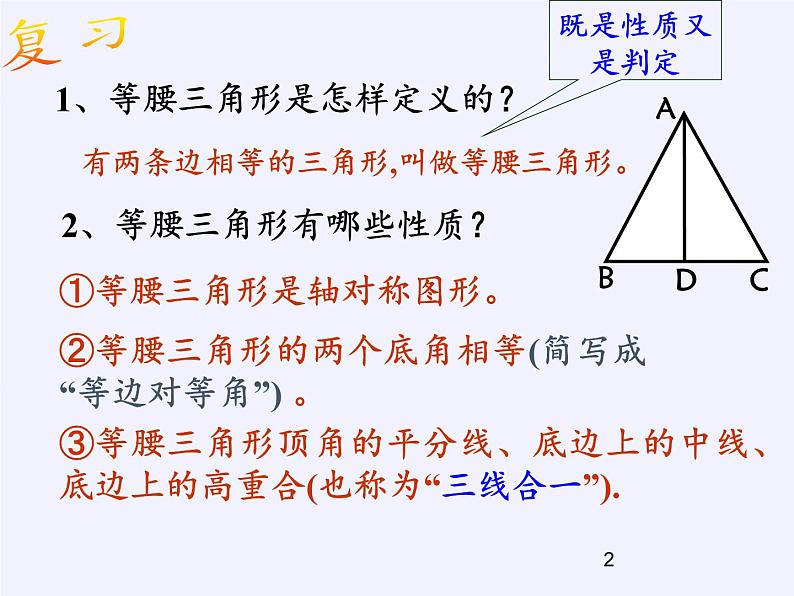
1、等腰三角形是怎样定义的？
有两条边相等的三角形,叫做等腰三角形。
①等腰三角形是轴对称图形。
③等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”).
②等腰三角形的两个底角相等(简写成“等边对等角”) 。
2、等腰三角形有哪些性质？
把“等腰三角形的两个底角相等”改写成“如果------那么-----”形式。
逆命题:如果一个三角形有两个角相等，那么这个三角形是等腰三角形.
如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
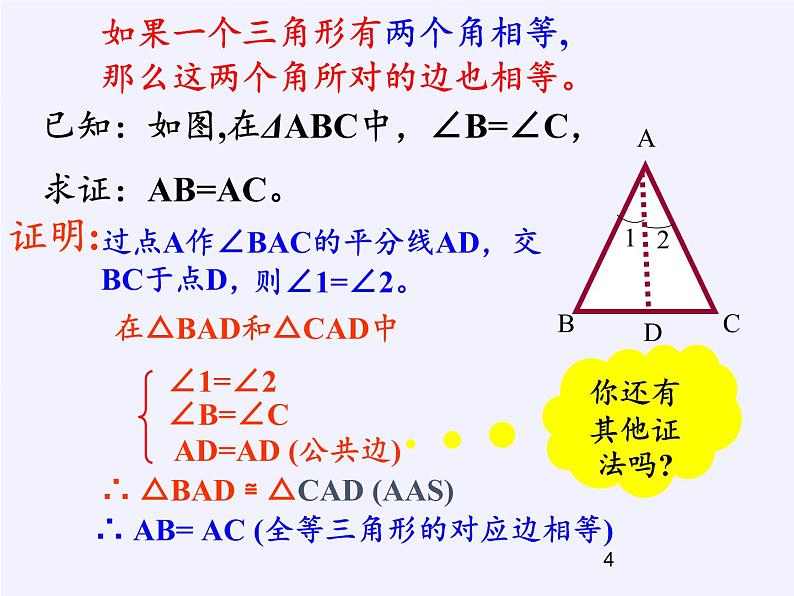
已知：如图,在ΔABC中，∠B=∠C，求证：AB=AC。
过点A作∠BAC的平分线AD，交BC于点D，
在△BAD和△CAD中
如果一个三角形有两个角相等,那么这两个角所对的边也相等。
AD=AD (公共边)
∴ AB= AC (全等三角形的对应边相等)
∴ △BAD ≌ △CAD (AAS)
已知：如图，在ΔABC中，∠B=∠C，求证：AB=AC。
过点A作AD⊥BC,垂足为D.
∴ ∠ADB=∠ADC（垂直的定义）
在△ABD和△ACD中
∴ AB=AC (全等三角形的对应边相等)
∴ △ABD ≌ △ACD (AAS)
如果一个三角形有两个角相等，那么这两个角所对的边也相等。
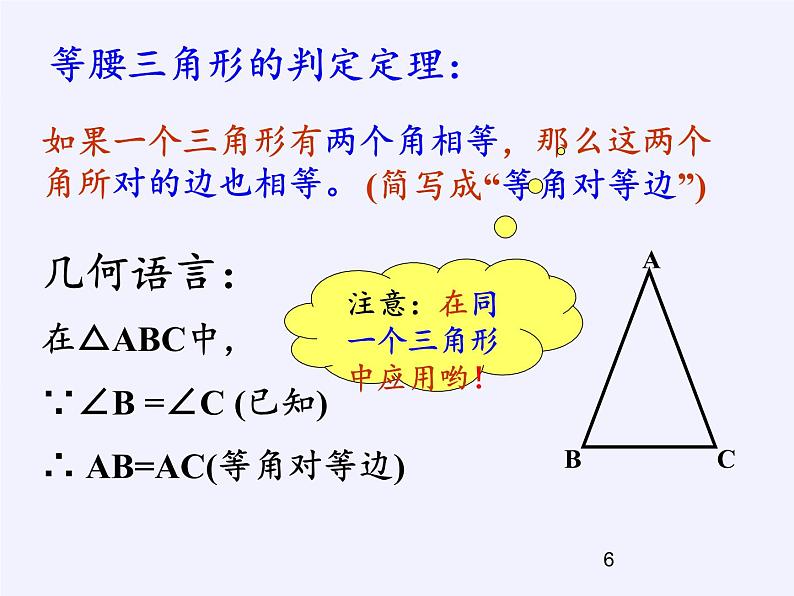
几何语言：在△ABC中，∵∠B =∠C (已知) ∴ AB=AC(等角对等边)
等腰三角形的判定定理：
(简写成“等角对等边”)
注意：在同一个三角形中应用哟！
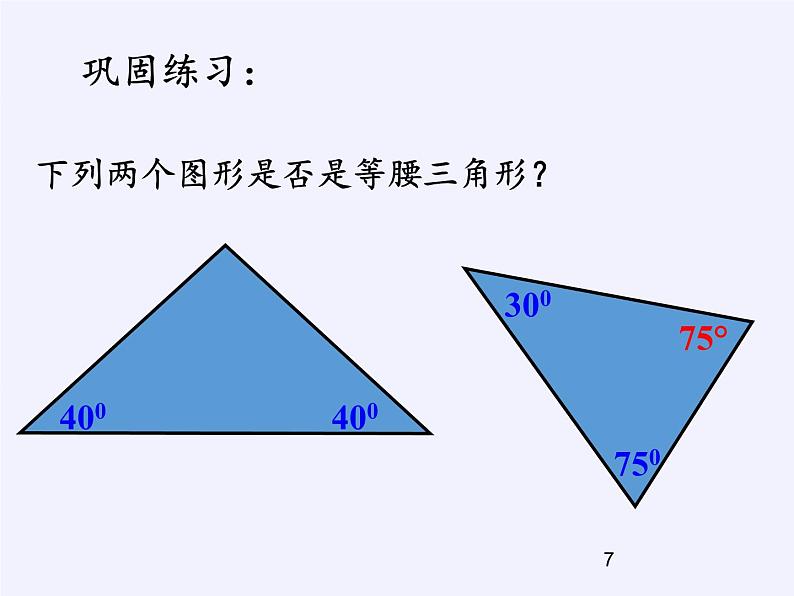
下列两个图形是否是等腰三角形？
例1、求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形。
如图，∠CAE是⊿ABC的外角，∠1=∠2，AD∥BC。
∵AD∥BC（已知）∴∠1=∠B（两直线平行，同位角相等） ∠2=∠C（两直线平行，内错角相等）∵∠1=∠2（已知）∴∠B=∠C（等量代换）∴AB=AC（等角对等边）
例2、如图,上午10 时，一艘轮船从A处出发以20海里每小时的速度向正北航行，中午12时到达B处，从A、B望灯塔C，测得∠NAC=40°，∠NBC=80°求从B处到灯塔C的距离。
解：∵∠NBC=∠A+∠C , ∠A = 40°∴∠C=∠NBC- ∠A= 80°- 40°= 40°∴ ∠C = ∠A∴ BA=BC（等角对等边）∵AB=20×（12-10）=40 （海里）∴BC=AB=40（海里）答：从B处到达灯塔C的距离为40海里。
一个三角形满足什么条件就是等边三角形?
①三个角都相等的三角形是等边三角形。
②有一个角等于60°的等腰三角形是等边三角形。
证明：∵∠A=∠B， ∴BC=AC(等角对等边) 又∵∠A=∠C， ∴BC=AB(等角对等边) ∴AB=BC=CA， 即△ABC是等边三角形。
已知：△ABC中，∠A=∠B=∠C。求证：△ABC是等边三角形。
三个角都相等的三角形是等边三角形。
证明:∵AB=AC,∠B=60°(已知),∴∠C=∠B=60°(等边对等角)∴∠A=60°(三角形内角和定理) ∴∠A=∠B =∠C=60° ∴△ABC是等边三角形(三个角都相等的三角形是等边三角形)
已知: 在△ABC中，AB=AC，∠B=60°．求证: △ABC是等边三角形。
第一种情况：有一个底角是60°；
有一个角等于60°的等腰三角形是等边三角形。
证明:∵AB=AC，∠A=60,∴∠C=∠B=60°(等边对等角) ∴∠A=∠B=∠C =60°，∴△ABC是等边三角形(三个角都相等的三角形是等边三角形)
第二种情况：顶角是60°；
已知: 如图,在△ABC中AB=AC,∠A=60°。求证: △ABC是等边三角形。
有一个角等于60°的等腰三角形是等边三角形.
2、三个角都相等的三角形是等边三角形。
3、有一个角是60°的等腰三角形是等边三角形。
1、三边都相等的三角形是等边三角形。(定义)
∵AB=BC=AC∴△ABC是等边三角形
∵ ∠B=600 AB=BC∴△ABC是等边三角形
∵ ∠A= ∠ B= ∠ C∴ AB=BC=AC∴△ABC是等边三角形
将两个含有30°的三角尺如图摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
结论：在直角三角形中，如果一个锐角等于 30°，那么它所对的直角边等于斜边的一半。
已知：如图，AD ∥BC，BD平分∠ABC, 求证：AB=AD.
证明：∵ AD ∥BC ∴∠ADB=∠DBC ∵ BD平分∠ABC ∴∠ABD=∠DBC ∴∠ABD=∠ADB ∴AB=AD
如图：在△ABC中，已知D为BC边的中点，DE⊥AB于点E，DF⊥AC于点F，且DE=DF，那么 AB=AC吗？
理由： ∵点 D为BC边的中点，
∴ DB=DC,
∵ DE⊥AB于点E，DF⊥AC于点F，
∴ △DEB和 △ DFC为直角三角形。
在Rt △DEB和 Rt △ DFC中，
∴ Rt△DEB ≌ △DFC (HL)
∴ ∠B= ∠C (全等三角形的对应角相等)
∴ AB= AC (等角对等边)
思考：若添加一个条件，使得△ABC是等边三角形，不再添加字母和线段，看你能说出多少个不同的添加。
如图：在△ABC中，已知D为BC边的中点，DE⊥AB于点E，DF⊥AC于点F，且DE=DF，那么AB=AC吗？
有两边相等的三角形是等腰三角形
两腰相等