

初中数学华师大版八年级上册5 边边边说课ppt课件
展开1、 全等三角形的定义
能够完全重合的两个三角形叫全等三角形。
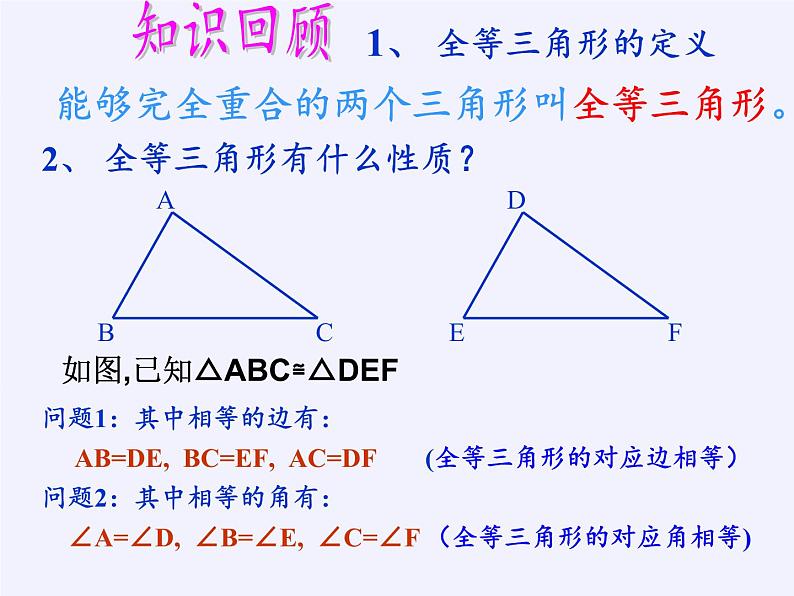
2、 全等三角形有什么性质?
问题1:其中相等的边有:
问题2:其中相等的角有:
AB=DE, BC=EF, AC=DF
∠A=∠D, ∠B=∠E, ∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
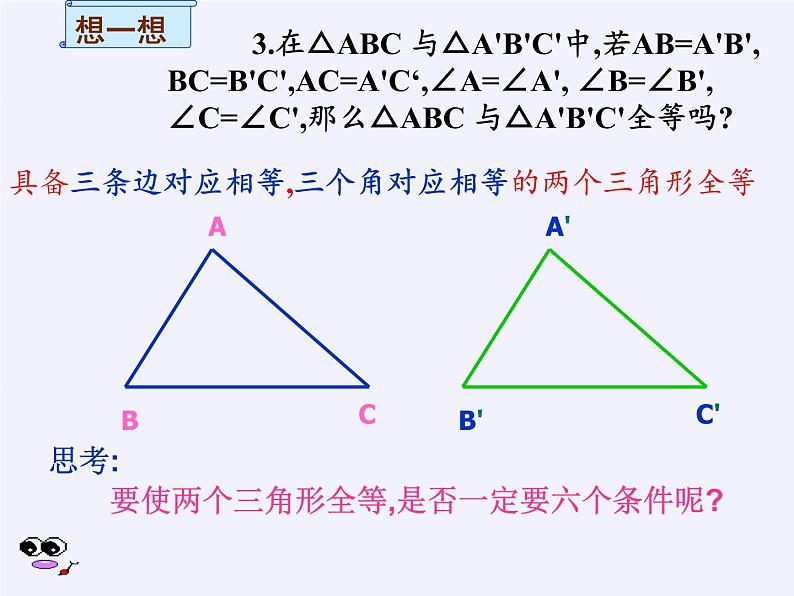
3.在△ABC 与△A'B'C'中,若AB=A'B',BC=B'C',AC=A'C‘,∠A=∠A', ∠B=∠B', ∠C=∠C',那么△ABC 与△A'B'C'全等吗?
具备三条边对应相等,三个角对应相等的两个三角形全等
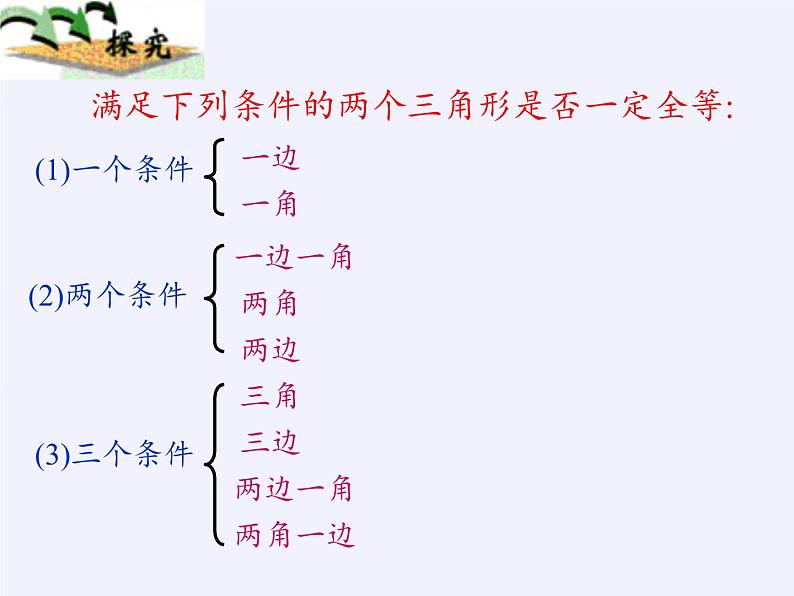
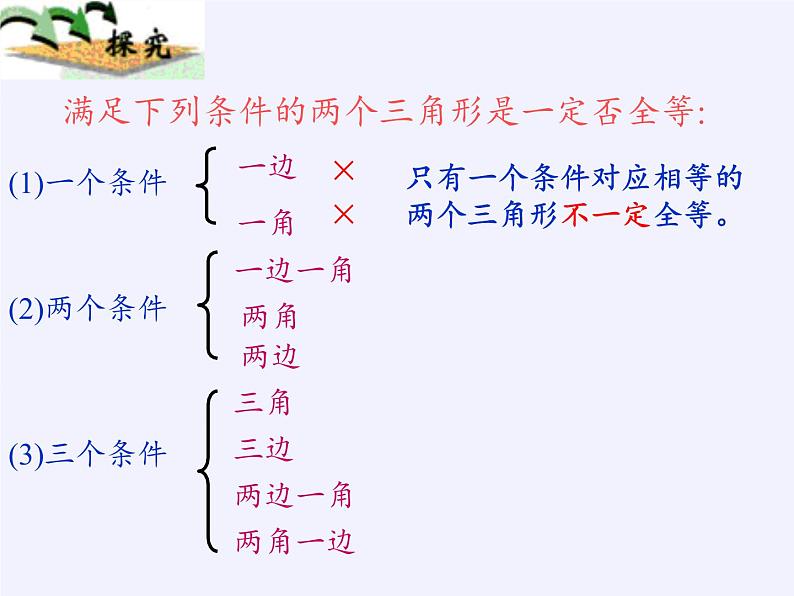
满足下列条件的两个三角形是否一定全等:
满足下列条件的两个三角形是一定否全等:
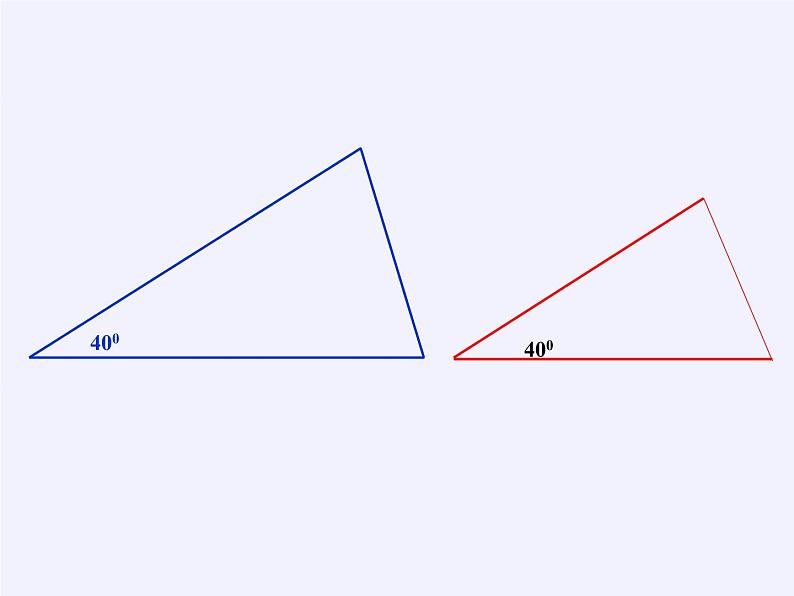
只有一个条件对应相等的两个三角形不一定全等。
只有两个条件对应相等的两个三角形不一定全等。
有三个条件对应相等的两个三角形有可能全等。
先任意画出一个△ABC,再画一个△ A’B’C’,使A’B’= AB ,B’C’ =BC,C’ A’= CA,把画好的△ A’B’C’剪下,放到出的△ABC上,它们全等吗?
三边对应相等的两个三角形全等( 可以简写为 “边边边”或“SSS”)。
想一想:这个结果反映了什么规律?
判断两个三角形全等的推理过程,叫做证明三角形全等。
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
例1. 如下图,△ABC是一个钢架, AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD
分析:要证明△ ABD≌ △ACD,首先要看这两个三角形的三条边是否对应相等。
证明: ∵D是BC中点, ∴BD=CD.
工人师傅常用角尺平分一个任意角, 做法 如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
分析:移动角尺,使角尺两边相同的刻度分别与M、N重合, 则 CM=CN.
如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC。
∴ BD-ED=CE-ED, 即BE=CD。
已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
解:要证明△ABC ≌△ FDE, 还应该有AB=DF这个条件
∵ DB是AB与DF的公共部分, 且AD=FB ∴ AD+DB=FB+DB 即 AB=FD
已知AC=FE,BC=DE,点A,B,D,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
(1)准备条件:证全等时要用的间接条件要先证好;
(2)证明三角形全等书写三步骤:
①写出在哪两个三角形中
②摆出三个条件用大括号括起来
证明三角形全等的步骤:
2. 三边对应相等的两个三角形全等(边边边或SSS);
1.知道三角形三条边的长度怎样画三角形,
通过本节课的学习,你有哪些收获?
祝贺你,在学习中获得了新知识!
数学八年级上册5 边边边教学课件ppt: 这是一份数学八年级上册5 边边边教学课件ppt,共25页。PPT课件主要包含了知识要点,新知导入,填一填,全等三角形,课程讲授,不一定全等,分别相等,SSS,边边边,随堂练习等内容,欢迎下载使用。
2020-2021学年5 边边边背景图课件ppt: 这是一份2020-2021学年5 边边边背景图课件ppt,共17页。PPT课件主要包含了复习导入,推进新课,SSS,应用表达式如图,练习提升,随堂演练,证明连结AC,公共边,想一想,这节课你有什么收获等内容,欢迎下载使用。
华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定5 边边边教学课件ppt: 这是一份华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定5 边边边教学课件ppt,共12页。PPT课件主要包含了知识回顾,不一定,探究新知,动手操作,几何语言,这节课你有什么收获等内容,欢迎下载使用。













