专题26 中心天体质量密度的计算问题 2022届高中物理常考点归纳二轮复习

这是一份专题26 中心天体质量密度的计算问题 2022届高中物理常考点归纳二轮复习，共10页。
常考点 中心天体质量和密度常用的估算方法
【典例1】
宇宙中两颗靠得比较近的星球，只受到彼此之间的万有引力作用绕两球心连线上某点绕转，称之为双星系
统。设某双星系统中A、B两星球绕其连线上的某固定点O做匀速圆周运动。若A、B的质量分别为M、m，
则（ ）
A．星球A与星球B的轨道半径之比为M：m
B．星球A与星球B的线速度大小之比为m：M
C．星球A与星球B的周期大小之比为m：M
D．若两星球间距离减小，则星球A做匀速圆周运动的周期变大
【解析】A、设双星A、B的轨道半径分别为r1 和 r2，间距为L
根据万有引力提供向心力，分别对双星列方程得：
＝Mω2r1
＝mω2r2
解得：r1＝，r2＝，
故A、B星球的轨道半径之比为：
，故A错误。
B、根据v＝ωr 可知，星球A的线速度与星球B的线速度之比为：
v1：v2＝r1：r2＝m：M，故B正确。
C、两星球同轴转动，做匀速圆周运动的角速度相等，即周期相等，故周期之比为1：1，故C错误。
D、根据T＝得：
T＝＝
故两星球的总质量一定，两星球之间的距离越小，其转动周期越小，故D错误。
【典例2】
天问一号于2021年2月10日实施火星捕获，将于2021年5月择机实施降轨软着陆火星表面。设天问一号
距火星表面高度约为火星半径的n倍，其环绕周期为T，引力常量为G，则火星的密度为（ ）
A．B．
C．D．
【解析】设火星的质量为M，天问一号的质量为m，根据万有引力提供向心力得：
解得：M＝
火星的密度为：
＝＝，故C正确，ABD错误。
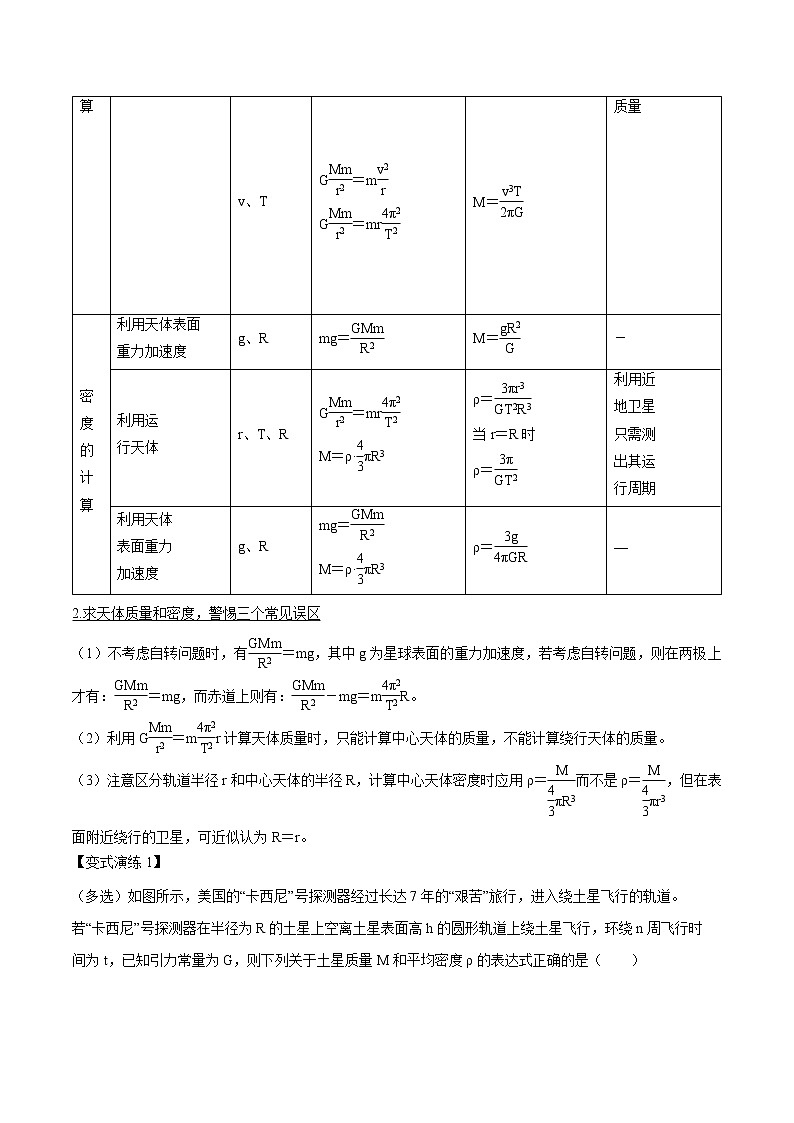
1.中心天体质量和密度常用的估算方法
2.求天体质量和密度，警惕三个常见误区
（1）不考虑自转问题时，有eq \f(GMm,R2)＝mg，其中g为星球表面的重力加速度，若考虑自转问题，则在两极上才有：eq \f(GMm,R2)＝mg，而赤道上则有：eq \f(GMm,R2)－mg＝meq \f(4π2,T2)R。
（2）利用Geq \f(Mm,r2)＝meq \f(4π2,T2)r计算天体质量时，只能计算中心天体的质量，不能计算绕行天体的质量。
（3）注意区分轨道半径r和中心天体的半径R，计算中心天体密度时应用ρ＝eq \f(M,\f(4,3)πR3)而不是ρ＝eq \f(M,\f(4,3)πr3)，但在表面附近绕行的卫星，可近似认为R＝r。
【变式演练1】
（多选）如图所示，美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行，进入绕土星飞行的轨道。
若“卡西尼”号探测器在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行，环绕n周飞行时
间为t，已知引力常量为G，则下列关于土星质量M和平均密度ρ的表达式正确的是（ ）
A．M＝B．M＝
C．ρ＝D．ρ＝
【解析】探测器绕土星飞行，环绕n周飞行时间为t，则探测器运行的周期：T＝
由万有引力提供向心力得：＝m
解得土星质量：M＝
根据密度公式可知，ρ＝
解得土星平均密度：ρ＝，故AD正确，BC错误。
【变式演练2】
2020年7月23日，中国首个火星探测器“天问一号”在海南文昌卫星发射中心发射升空。该探测器经过多
次变轨，进入环火轨道，预计5月中旬，将择机开展着陆、巡视等任务，进行火星科学探测。假设在火星
表面完成下面的实验：在固定的竖直光滑圆轨道内部最低点静止放置一个质量为m的小球（可视为质点），
如图所示，当给小球一水平向右的瞬时冲量I时，小球恰好能在竖直平面内做完整的圆周运动。若已知圆轨道半径为r，火星的半径为R、万有引力常量为G，则火星的质量为（ ）
A．B．
C．D．
【解析】设火星表面的重力加速度为g，小球在最高点的速度为v1，根据动量定理I＝mv得：
小球在最低点的速度：v＝①
对小球从最低点到最高点根据动能定理得：
﹣mg2r＝②
小球刚好做完整的圆周运动，在最高点有：
mg＝③
由①②③解得：g＝
在火星表面，根据万有引力等于重力得：
解得：M＝＝，故D正确，ABC错误。
拓展练习
1．“嫦娥五号”月球探测器实现了人类首次月球背面软着陆和巡视勘察。“嫦娥五号”月球探测器在月球上空巡视可看成匀速圆周运动，其轨道半径为r，运动周期为T。已知地球质量为M1、半径为R1、表面的重力加速度为g，月球质量为M2、半径为R2，两者均可视为质量分布均匀的球体。则月球表面的重力加速度为（ ）
A．B．
C．D．
【解析】AB、在月球表面的物体所受重力等于万有引力，①
在地球表面的物体所受重力等于万有引力，②
联立①②可得：g月＝，故AB错误；
CD、嫦娥五号绕月做圆周运动，由万有引力提供向心力得，
解得月球质量③
联立①③可得：，故C正确，D错误。
2．2021年2月24日，我国首个火星探测器“天问一号”成功进入火星的停泊轨道，正式开启了环绕火星阶段的探测任务。若探测器在离火星表面高度为h、近似为圆形的轨道上运行，周期为T，已知火星半径为R，万有引力常量为G，则火星的密度为（ ）
A．B．
C．D．
【解析】对探测器做圆周运动，万有引力提供向心力：，M为火星质量，火星的密度为：ρ＝，火星的体积：V＝
联立解得：ρ＝，故ABD错误，C正确。
3．2020年10月诺贝尔物理学奖一半被授予英国科学家罗杰彭罗斯（Rger Penrse）以表彰他在黑洞研究方面的贡献。光无法从密度极大、引力极大的天体中逃逸，这种天体称为黑洞。已知地球公转的半径为R，周期约为T，光速为c，地面的重力加速度为g。假设太阳演变为黑洞，（设太阳的质量不变，逃逸速度是其第一宇宙速度的倍，G为引力常量）（ ）
A．地球的质量为
B．地球的逃逸速度为
C．太阳的质量为
D．太阳演变为黑洞的最大半径为
【解析】A、在地球表面上，质量为m的物体受到重力等于地球对物体的万有引力，则G＝mg，可得地球的质量为M地＝＜，（式中R地是地球的半径），故A错误；
B、设地球的第一宇宙速度为v1，根据万有引力等于向心力，得G＝mg＝m，得v1＝
地球的逃逸速度是其第一宇宙速度的倍，则地球的逃逸速度为v3＝v1＝＜，故B错误；
C、地球绕太阳公转时，根据万有引力等于向心力，得G＝M地R，可得太阳的质量为M日＝，故C错误；
D、太阳演变为黑洞，第一宇宙速度设为v1′，它的半径为R'，则有v1′＝
据题有v1′≥c，结合M日＝，联立可得R′≤，所以，太阳演变为黑洞的最大半径为，故D正确。
4．我国计划在2030年之前可制造出可以水平起飞、水平着落并且可以多次使用的航天飞机，假设一航天员乘坐一航天飞机着落到某一个星球后，在该星球表面以大小为v0的速度竖直向上抛出一物体，经过时间t后物体落回抛出点。已知该星球的半径为R，该星球没有大气层，也不自转。则该星球的第一宇宙速度大小为（ ）
A．B．C．D．
【解析】根据物体做竖直上抛运动的速度﹣时间关系可知，t＝，所以星球表面的重力加速度g＝。
星球表面重力与万有引力相等，mg＝，近地卫星的轨道半径为R，由万有引力提供圆周运动向心力有：＝m，
联立解得该星球的第一宇宙速度：v＝，故C正确，ABD错误。
5．2019年1月3日，嫦娥四号成为全世界第一个在月球背面成功实施软着陆的探测器。嫦娥四号着陆前，在离月球表面高h的圆形轨道上运行n圈所用时间为t，月球半径为R，引力常量为G，则可求得月球的质量为（ ）
A．B．
C．D．
【解析】嫦娥四号着陆前，在半径为r＝R+h的圆形轨道上运行n圈所用时间为t，则运行周期T＝，
根据万有引力提供向心力可知，，
解得月球质量M＝，故B正确，ACD错误。
6．人类探索星辰大海的步伐从未停止，2021年，包括我国“天问一号”在内的火星探测器已经或即将在火星登陆。若探测器登陆前绕火星运行的过程可以近似看成匀速圆周运动，探测器所搭载的传感器测定t时间内探测器绕火星飞行的路程是s，探测器与火星中心的连线转过的角度为θ，已知引力常量为G，火星半径为r，则（ ）
A．探测器的加速度为
B．火星的质量为
C．火星的质量为
D．火星的密度为
【解析】A、探测器的线速度，探测器的角速度，探测器的加速度，故A错误；
BC、探测器的轨道半径r1＝，
根据万有引力提供向心力可得：
联立解得火星的质量M＝，故BC错误；
D、火星的密度，故D正确。
7．为了测量某行星的质量和半径，宇航员记录了登陆舱在该行星表面附近做圆周运动的周期T，登陆舱在行星表面着陆后，用弹簧秤测量一个质量为m的砝码静止时读数为N，已知引力常量为G，则下列计算中错误的是（ ）
A．该行星的半径为
B．该行星的质量为
C．该行星的密度为
D．在该行星的第一宇宙速度为
【解析】AB、登陆舱在该行星表面做圆周运动，万有引力提供向心力，故：＝m①
在星球表面，用弹簧秤称量一个质量为m的砝码读数为N，故：N＝②
联立解得：M＝，R＝，故A正确，B错误。
C、行星的密度：ρ＝＝，故C正确。
D、第一宇宙速度是星球表面轨道卫星的环绕速度，故v＝＝，故D正确。
8．（多选）若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球，测出小球从抛出到落地的位移为L，已知月球半径为R，万有引力常量为G，则下列说法正确的是（ ）
A．月球表面的重力加速度g月＝
B．月球的质量m月＝
C．月球的第一宇宙速度v＝v0
D．月球的平均密度ρ＝
【解析】A、小球做平抛运动，水平位移为：x＝，则平抛运动的时间为：t＝＝，竖直方向上，h＝gt2，得月球表面的重力加速度为：g月＝2，故A错误；
B、物体在月球表面，根据重力等于万有引力，有：G＝mg月，解得月球的质量为：m月＝，故B错误；
C、在月球表面，根据重力充当向心力可知：mg月＝m ，解得月球的第一宇宙速度为：v＝v0，故C正确；
D、月球的平均密度为：ρ＝＝，故D错误。质
量
的
计
算
使用方法
已知量
利用公式
表达式
备注
利用运
行天体
r、T
Geq \f(Mm,r2)＝mreq \f(4π2,T2)
M＝eq \f(4π2r3,GT2)
只能得
到中心
天体的
质量
r、v
Geq \f(Mm,r2)＝meq \f(v2,r)
M＝eq \f(rv2,G)
v、T
Geq \f(Mm,r2)＝meq \f(v2,r)
Geq \f(Mm,r2)＝mreq \f(4π2,T2)
M＝eq \f(v3T,2πG)
密
度
的计
算
利用天体表面
重力加速度
g、R
mg＝eq \f(GMm,R2)
M＝eq \f(gR2,G)
－
利用运
行天体
r、T、R
Geq \f(Mm,r2)＝mreq \f(4π2,T2)
M＝ρ·eq \f(4,3)πR3
ρ＝eq \f(3πr3,GT2R3)
当r＝R时
ρ＝eq \f(3π,GT2)
利用近
地卫星
只需测
出其运
行周期
利用天体
表面重力
加速度
g、R
mg＝eq \f(GMm,R2)
M＝ρ·eq \f(4,3)πR3
ρ＝eq \f(3g,4πGR)
—