北京课改版七年级下册第六章 整式的运算综合与测试课时训练

京改版七年级数学下册第六章整式的运算定向攻克

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、如果a﹣4b＝0，那么多项式2（b﹣2a+10）+7（a﹣2b﹣3）的值是（　　）

A．﹣1 B．﹣2 C．1 D．2

2、数左手手指，1为大拇指，数到第2011时对应的手指是（　　）

A．无名指 B．食指 C．中指 D．大拇指

3、下列运算正确的是（    ）

A．a3•a3＝a9 B．a5÷a3＝a2 C．（a3）2＝a5 D．（a2b）3＝a2b3

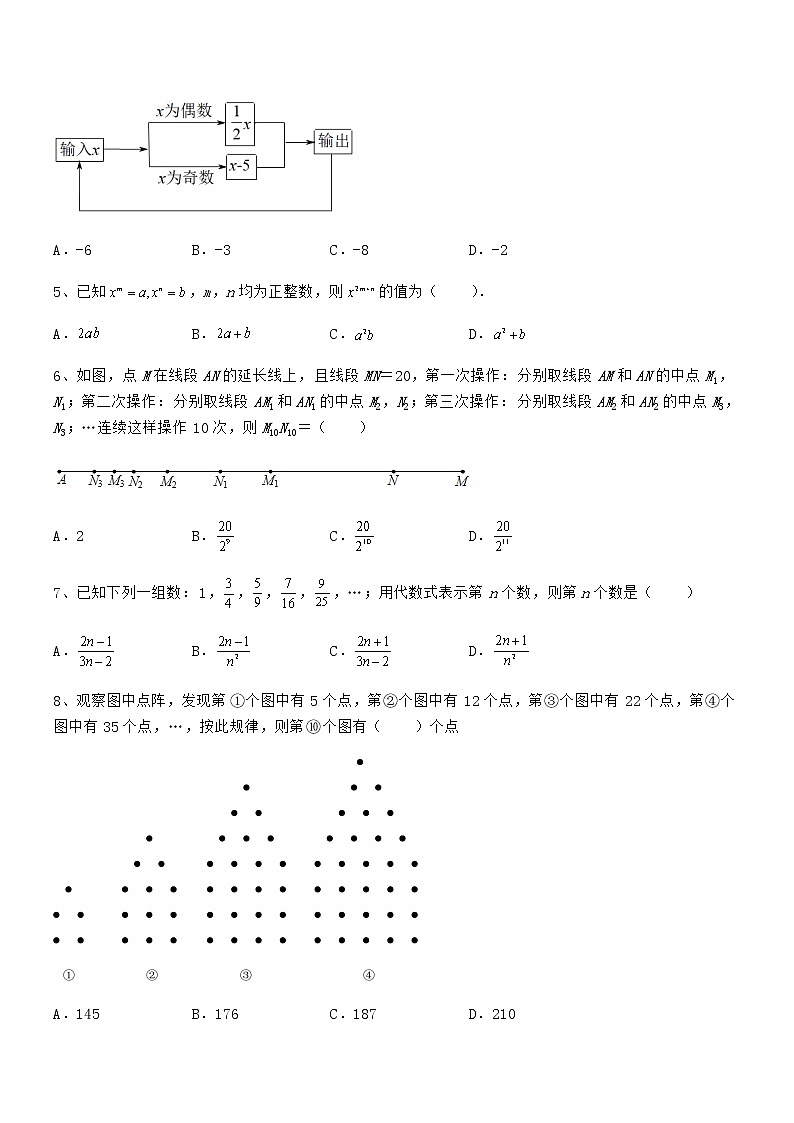
4、如图所示的运算程序中，若开始输入x的值为2，则第2022次输出的结果是（   ）

A．-6 B．-3 C．-8 D．-2

5、已知，m，n均为正整数，则的值为（    ）．

A． B． C． D．

6、如图，点M在线段AN的延长线上，且线段MN＝20，第一次操作：分别取线段AM和AN的中点M1，N1；第二次操作：分别取线段AM1和AN1的中点M2，N2；第三次操作：分别取线段AM2和AN2的中点M3，N3；…连续这样操作10次，则M10N10＝（　　）

A．2 B． C． D．

7、已知下列一组数：1，，，，，…；用代数式表示第n个数，则第n个数是（　　）

A． B． C． D．

8、观察图中点阵，发现第①个图中有5个点，第②个图中有12个点，第③个图中有22个点，第④个图中有35个点，…，按此规律，则第⑩个图有（　　）个点

A．145 B．176 C．187 D．210

9、若，，，则的值为（    ）

A． B． C．1 D．

10、单项式的系数和次数分别是（    ）

A．－2，5 B．，5 C．，2 D．，2

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、一只昆虫从点A处出发，以每分钟2米的速度在一条直线上运动，它先前进1米，再后退2米，又前进3米，再后退4米，…依此规律继续走下去，则运动1小时时这只昆虫与A点相距______米．

2、多项式的次数是____次，它的常数项是____．

3、黑白两种颜色的纸片，按如图所示的规律拼成若干个图案，第n个图形有白纸片____________张．

4、单项式的次数是_____________．

5、若a与b互为相反数，c与d互为倒数，则2a+2b+5cd＝_____．

三、解答题（5小题，每小题10分，共计50分）

1、先化简再求值：

（1），其中a=1，b=2．

（2），其中x=．

2、计算：．

3、先化简，再求值2a2﹣[（ab﹣4a2）＋8ab]﹣ab；其中a＝1，b＝﹣．

4、如图1是一个长为、宽为的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

（1）观察图2，请你直接写出下列三个代数式之间的等量关系为_______；

（2）运用你所得到的公式解答下列问题：

①若为实数，且，，求的值．

②如图3，，分别表示边长为的正方形的面积，且三点在一条直线上，若，求图中阴影部分的面积．

5、如图所示，用三种大小不同的5个正方形和一个长方形（阴影部分）拼成长方形ABCD，其中厘米，最小的正方形的边长为x厘米．

（1）________厘米，________厘米（用含x的整式分别表示）；

（2）求长方形ABCD的周长（用含x的整式表示），当厘米时，求其值．

---------参考答案-----------

一、单选题

1、A

【分析】

利用整式的加减计算法则和去括号法则化简，由此求解即可．

【详解】

解：∵，

∴

，

故选A．

【点睛】

本题主要考查了整式的加减--化简求值，去括号，熟知相关计算法则是解题的关键．

2、C

【分析】

根据题意可得：：第一次是五个数，以后每一次都是四个数，所以先减去1，可得每两个循环是“食指、中指、无名指、小拇指、无名指、中指、食指、大拇指”，从而得到2011是从2开始的第2011﹣1＝2010个数，可得2011是第503个循环组的第2个数，即可求解．

【详解】

解：根据题意得：第一次是五个数，以后每一次都是四个数，所以先减去1，可得每两个循环是“食指、中指、无名指、小拇指、无名指、中指、食指、大拇指”，

∵2011是从2开始的第2011﹣1＝2010个数，

∴2010÷8＝251…2，

∴2011是第252个循环组的第2个数，

∴第2011与3的位置相同，即中指的位置．

故选：C

【点睛】

本题主要考查了数字类规律题，明确题意，准确得到规律是解题的关键．

3、B

【分析】

直接利用积的乘方运算法则、同底数幂的乘除运算法则分别判断得出答案．

【详解】

解：A．a3•a3＝a6，故此选项不合题意；

B．a5÷a3＝a2，故此选项符合题意；

C．（a3）2＝a6，故此选项不合题意；

D．（a2b）3＝a6b3，故此选项不合题意；

故选：B．

【点睛】

此题主要考查了积的乘方运算、同底数幂的乘除运算，正确掌握相关运算法则是解题关键．

4、B

【分析】

先分别求出第1-8次输出的结果，再归纳类推出一般规律，由此即可得出答案．

【详解】

解：第1次输出的结果为；

第2次输出的结果为；

第3次输出的结果为；

第4次输出的结果为；

第5次输出的结果为；

第6次输出的结果为；

第7次输出的结果为；

第8次输出的结果为，

…，

由此可知，从第2次开始，输出的结果是以−4，−2，−1，−6，−3，−8循环往复的，

因为，

所以第2022次输出的结果与第6次输出的结果相同，即为−3，

故选：B．

【点睛】

本题考查了程序流程图与代数式求值，正确归纳类推出一般规律是解题关键．

5、C

【分析】

根据幂的乘方和同底数幂的乘法运算法则进行计算即可得出结果．

【详解】

解：∵

∴

故选C

【点睛】

本题主要考查了幂的乘方和同底数幂的乘法，熟练掌握相关运算法则是解答本题的关键．

6、C

【分析】

根据线段中点定义先求出M1N1的长度，再由M1N1的长度求出M2N2的长度，从而找到MnNn的规律，即可求出结果．

【详解】

解：∵线段MN＝20，线段AM和AN的中点M1，N1，

∴M1N1＝AM1﹣AN1

＝AM﹣AN

＝（AM﹣AN）

＝MN

＝×20

＝10．

∵线段AM1和AN1的中点M2，N2；

∴M2N2＝AM2﹣AN2

＝AM1﹣AN1

＝（AM1﹣AN1）

＝M1N1

＝××20

＝×20

＝5．

发现规律：

MnNn＝×20，

∴M10N10＝×20．

故选：C．

【点睛】

本题考查两点间的距离，根据线段中点的定义得出MnNn＝×20是解题关键．

7、B

【分析】

根据题意仔细观察给出的数字，找出其中存在的规律从而解题即可．

【详解】

解：∵1＝；

；

；

∴第n个数是：.

故选：B．

【点睛】

本题考查数字找规律，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．

8、B

【分析】

根据已知图形得第个图形中黑点数为，据此求解可得．

【详解】

解：图①中黑点的个数，

图②中黑点的个数，

图③中黑点的个数，

第个图形中黑点的个数为，

第⑩个图形中黑点的个数为．

故选：B．

【点睛】

本题主要考查图形的变化规律，解题的关键是根据已知图形得出第个图形中黑点的个数为．

9、D

【分析】

根据同底数幂的除法的逆运算及幂的乘方的逆运算解答．

【详解】

解：∵，，

∴==3÷8=，

故选D．

【点睛】

本题考查了同底数幂的除法的逆运算及幂的乘方的逆运算，解题的关键是熟练掌握运算法则．

10、B

【分析】

根据单项式系数及次数定义解答．

【详解】

解：单项式的系数和次数分别是，2+1+2=5，

故选：B．

【点睛】

此题考查了单项式的次数及系数的定义，熟记定义是解题的关键．

二、填空题

1、8

【分析】

由于这只昆虫的速度为2米分钟，所以“前进1米，再后退2米”共用了1.5分钟，此时实际上向后只退了一米；“前进3米，再后退4米”共用了3.5分钟，此时实际上也只向后退了一米．由此不难看出，后一次运动比前一次多用2分钟，每次实际上都是向后退一米．然后根据规律列式计算即可．

【详解】

解：1小时分，

规定昆虫每前进一次和后退一次为一运动周期，则设昆虫的运动周期数为，每一周期所用总时间为．

设每周期前进的距离为，则；

由题意可得：；

假设昆虫运动所用总时间为；则；

当分时，代入上式中可得但还剩余7.5分钟，由公式可得第8周需要15.5分钟，但是每一周期中后退时间比前进时间多0.5分钟，所以在第8周期中前进时间为7.5分钟，后退时间为8分钟．

由于运动一个周期后退一米，所以运动7个周期就后退7米，由于在60分钟内运动完7周期后正好剩余7.5分钟，这样在第8周期就正好前进的距离米，故运动1小时时这只昆虫与点相距为米．

故填8．

【点睛】

本题主要考查代数式规律问题，认真审题，找出规律，是解决此类问题的关键所在．

2、3    -5   

【分析】

根据多项式中常数项（多项式中，不含字母的项即为常数项）和次数（多项式中最高次项的次数）的定义求解即可．

【详解】

解：中，次数是3次，常数项为-5，

故答案为：3；-5．

【点睛】

题目主要考查多项式中常数项与次数的定义，理解这两个定义是解题关键．

3、（3n+1）n)

【分析】

先求出每一个图形的白色纸片的块数，找出规律，后一个图形比前一个图形的白色纸片多3块，然后总结出第n个图形的表示纸片的块数；

【详解】

解：第1个图形有白色纸片有：4＝3+1块，

第2个图形有白色纸片有：7＝3×2+1块，

第3个图形有白色纸片有：10＝3×3+1块，

…，

第n个图形有白色纸片：3n+1块，

故答案为：（3n+1）．

【点睛】

本题考查了图形的变化规律，观察出后一个图形比前一个图形的白色纸片的块数多3块，从而总结出第n个图形的白色纸片的块数是解题的关键．

4、3

【分析】

根据单项式的次数的定义得出即可．

【详解】

解：单项式的次数是1+2=3，
故答案为：3．

【点睛】

本题考查了单项式的次数的定义，能熟记单项式的次数的定义的内容是解此题的关键，注意：单项式中的字母的指数的和，叫单项式的次数．

5、5

【分析】

根据互为相反数的和为0，互为倒数的积为1，代入计算即可．

【详解】

解：∵a与b互为相反数，c与d互为倒数，

∴，，

2a+2b+5cd＝；

故答案为：5．

【点睛】

本题考查了相反数和倒数，有理数的运算，解题关键是明确互为相反数的和为0，互为倒数的积为1．

三、解答题

1、（1），2；（2），．

【解析】

【分析】

（1）先去括号，再计算整式的加减，然后将的值代入计算即可得；

（2）先去括号，再计算整式的加减，然后将的值代入计算即可得．

【详解】

解：（1）原式，

，

将代入得：原式；

（2）原式，

，

将代入得：原式．

【点睛】

本题考查了整式加减中的化简求值，熟练掌握整式的加减运算法则是解题关键．

2、

【解析】

【分析】

根据整式的乘法运算法则、合并同类项法则进行计算即可．

【详解】

解：

=

=．

【点睛】

本题考查整式的乘除、合并同类项，熟练掌握运算法则是解答的关键．

3、，7．

【解析】

【分析】

先去括号，再计算整式的加减，然后将的值代入计算即可得．

【详解】

解：原式，

，

，

将代入得：原式．

【点睛】

本题考查了整式加减中的化简求值，熟练掌握整式加减的运算法则是解题关键．

4、（1）（a+b）2＝4ab+（a﹣b）2；（2）①m﹣n＝4或m﹣n＝﹣4；②阴影部分面积为8．

【解析】

【分析】

（1）结合图形可得：大正方形面积＝四个矩形的面积+中间小正方形的面积，表示出各个图形的面积，三者关系式即可得；

（2）①根据（1）中结论可得：，然后将已知式子的值代入化简即可；

②根据题意可得：，且，将其代入完全平方公式中化简可得：，结合图形，求阴影部分面积即可．

【详解】

解：

（1）由图可知，

大正方形面积＝四个矩形的面积+中间小正方形的面积，

即，

故答案为：；

（2）①∵，，

∴，

∴，

∴或；

②∵，分别表示边长为p，q的正方形的面积，

∴，，

∵，

∴，

∵，

∴

∴，,

∴，

由图可知，阴影部分面积为：，

∴阴影部分面积为8．

【点睛】

题目主要考查完全平方公式在求几何图形面积中的应用，理解题意，结合图形，熟练运用两个完全平方公式的变形是解题关键．

5、（1）,；（2），158cm．

【解析】

【分析】

（1）根据图形可得结合线段的和差、正方形的性质即可解答；

（2）分别表示出AB和BC，然后再表示出周长，最后将x=9代入计算．

【详解】

解：（1）由图可知：FG＝厘米，DG＝厘米；

故答案是：，；

（2）长方形的宽为：，长为：，

则长方形ABCD的周长为：，

当时，．

【点睛】

本题主要考查了列代数式和代数式求值，理解各个图形的边长之间的数量关系是解答本题的关键．