初中数学北京课改版七年级下册第七章 观察、猜想与证明综合与测试一课一练

这是一份初中数学北京课改版七年级下册第七章 观察、猜想与证明综合与测试一课一练，共22页。试卷主要包含了下列说法中正确的是，命题，下列命题中，为真命题的是，一个角的补角比这个角的余角大．等内容，欢迎下载使用。
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，货轮O航行过程中，同时发现灯塔A和轮船B，灯塔A在货轮O北偏东40°的方向，∠AOE＝∠BOW，则轮船B在货轮（ ）
A．西北方向B．北偏西60°C．北偏西50°D．北偏西40°
2、已知∠A＝37°，则∠A的补角等于（ ）
A．53°B．37°C．63°D．143°
3、已知一个角等于它的补角的5倍，那么这个角是（ ）
A．30°B．60°C．45°D．150°
4、在证明命题“若，则”是假命题时，下列选项中所举反例不正确的是（ ）
A．B．C．D．
5、下列说法中正确的是（ ）
A．一个锐角的补角比这个角的余角大90°B．－a表示的数一定是负数
C．射线AB和射线BA是同一条射线D．如果︱x︱＝5，那么x一定是5
6、命题：①对顶角相等；②在同一平面内，垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等．其中假命题有（ ）
A．0个B．1个C．2个D．3个
7、下列命题中，为真命题的是（ ）
A．若，则B．若，则
C．同位角相等D．对顶角相等
8、如图，点D是AB上的一点，点E是AC边上的一点，且∠B＝70°，∠ADE＝70°，∠DEC＝100°，则∠C是( )
A．70°B．80°C．100°D．110°
9、一个角的补角比这个角的余角大（ ）．
A．70°B．80°C．90°D．100°
10、已知∠α的两边分别平行于∠β的两边．若∠α＝60°，则∠β的大小为（ ）
A．30°B．60°C．30°或60°D．60°或120°
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
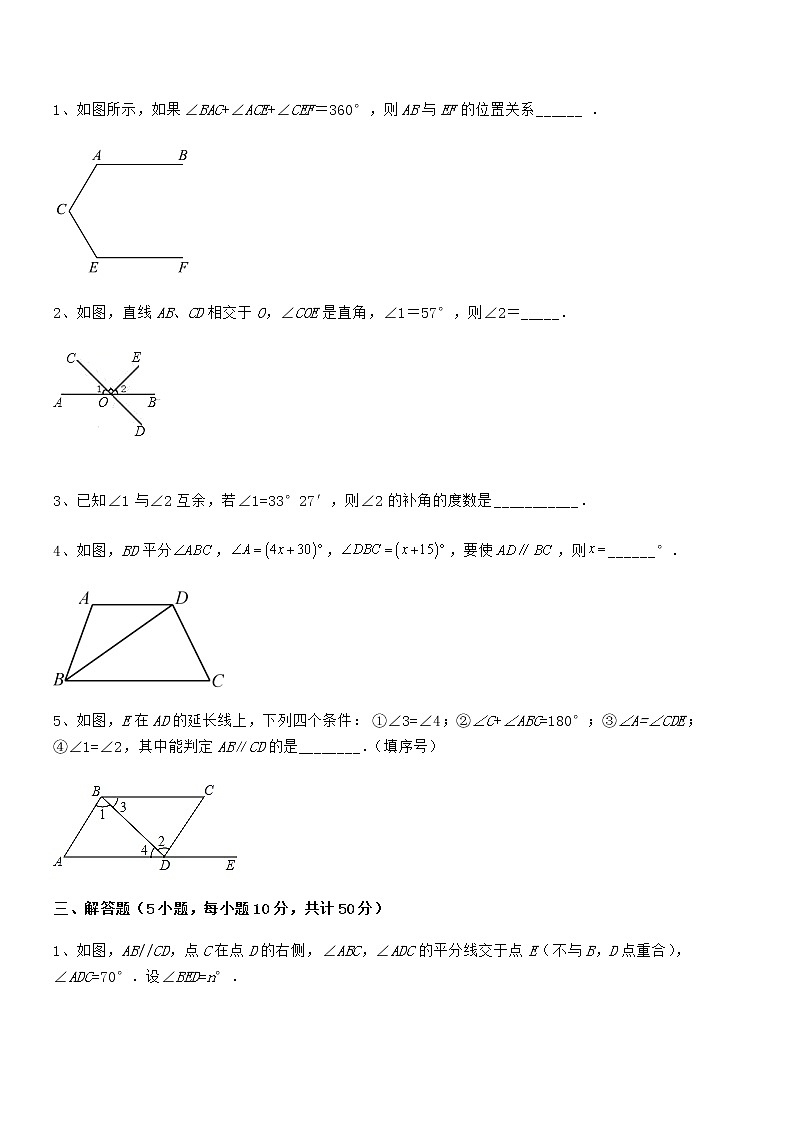
1、如图所示，如果∠BAC+∠ACE+∠CEF＝360°，则AB与EF的位置关系______ ．
2、如图，直线AB、CD相交于O，∠COE是直角，∠1＝57°，则∠2＝_____．
3、已知∠1与∠2互余，若∠1=33°27′，则∠2的补角的度数是___________．
4、如图，BD平分，，，要使，则______°．
5、如图，E在AD的延长线上，下列四个条件：①∠3=∠4；②∠C+∠ABC=180°；③∠A=∠CDE；④∠1=∠2，其中能判定AB∥CD的是________．（填序号）
三、解答题（5小题，每小题10分，共计50分）
1、如图，AB//CD，点C在点D的右侧，∠ABC，∠ADC的平分线交于点E（不与B，D点重合），∠ADC=70°．设∠BED=n°．
（1）若点B在点A的左侧，求∠ABC的度数（用含n的代数式表示）；
（2）将（1）中的线段BC沿DC方向平移，当点B移动到点A右侧时，请画出图形并判断∠ABC的度数是否改变．若改变，请求出∠ABC的度数（用含n的代数式表示）；若不变，请说明理由．
2、如图，直线DE上有一点O，过点O在直线DE上方作射线OC，∠COE比它的补角大100°，将一直角三角板AOB的直角点放在点O处，一条直角边OA在射线OD上，另一边OB在直线DE上方，将直角三角板绕点O按每秒10°的速度逆时针旋转一周．设旋转时间为t秒．
（1）求∠COE的度数；
（2）若射线OC的位置保持不变，在旋转过程中，是否存在某个时刻，使得∠BOC＝∠BOE？若存在，请求出t的取值，若不存在，请说明理由；
（3）若在三角板开始转动的同时，射线OC也绕O点以每秒10°的速度顺时针旋转一周．从旋转开始多长时间．射线OC平分∠BOE．直接写出t的值．（本题中的角均为大0°且小180°的角）
3、完成下面的证明．
如图，已知AD⊥BC，EF⊥BC，∠1＝∠2，求证：∠BAC+∠AGD＝180°．
证明：∵AD⊥BC，EF⊥BC（已知），
∴∠EFB＝90°，∠ADB＝90°（ ），
∴∠EFB＝∠ADB（等量代换），
∴EFAD（ ），
∴∠1＝∠BAD（ ），
又∵∠1＝∠2（已知），
∴∠2＝∠ （等量代换），
∴DGBA（内错角相等，两直线平行），
∴∠BAC+∠AGD＝180°（ ）．
4、如图，点A，O，B在同一条直线上，，分别平分和．
（1）求的度数．
（2）如果，求的度数．
5、如图，是的平分线，是的平分线．
（1）若，，求的度数；
（2）若与互补，且，求的度数．
---------参考答案-----------
一、单选题
1、D
【分析】
根据题意得：∠AON=40°，再由等角的余角相等，可得∠BON=∠AON=40°，即可求解．
【详解】
解：根据题意得：∠AON=40°，
∵∠AOE＝∠BOW，∠AON+∠AOE=90°，∠BON+∠BOW=90°，
∴∠BON=∠AON=40°，
∴轮船B在货轮的北偏西40°方向．
故选：D
【点睛】
本题主要考查了余角的性质，方位角，熟练掌握等角的余角相等是解题的关键．
2、D
【分析】
根据补角的定义：如果两个角的度数和为180度，那么这两个角互为补角，进行求解即可．
【详解】
解：∵∠A=37°，
∴∠A的补角的度数为180°-∠A=143°，
故选D．
【点睛】
本题主要考查了求一个角的补角，熟知补角的定义是解题的关键．
3、D
【分析】
列方程求出这个角即可．
【详解】
解：设这个角为x，
列方程得：x＝5（180°−x）
解得x＝150°．
故选：D．
【点睛】
本题考查了补角，若两个角的和等于180°，则这两个角互补，列方程求出这个角是解题的关键．
4、A
【分析】
所谓举反例是指满足命题的条件但不满足命题的结论，由此可判断．
【详解】
显然A选项既满足命题的条件也满足命题的结论，故不是举反例，其它三个选项满足命题的条件，但不满足命题的结论，所以都是举反例；
故选：A
【点睛】
本题考查了命题的真假，说明一个命题是假命题要举反例．掌握举反例的含义是关键．
5、A
【分析】
根据补角和余角的概念即可判断A选项；根据负数的概念即可判断B选项；根据射线的概念即可判断C选项；根据绝对值的意义即可判断D选项．
【详解】
解：A、设锐角的度数为x ，
∴这个锐角的补角为，这个锐角的余角为，
∴．
故选项正确，符合题意；
B、当时，，
∴－a表示的数不一定是负数，
故选项错误，不符合题意；
C、射线AB是以A为端点，沿AB方向延长的的射线，射线BA是以B为端点，沿BA方向延长的的射线，
∴射线AB和射线BA不是同一条射线，
故选项错误，不符合题意；
D、如果︱x︱＝5，，
∴x不一定是5，
故选项错误，不符合题意，
故选：A．
【点睛】
此题考查了补角和余角的概念，负数的概念，射线的概念，绝对值的意义，解题的关键是熟练掌握以上概念和性质．
6、C
【分析】
利用对顶角的性质、平行线的性质分别进行判断后即可确定正确的选项．
【详解】
解：①对顶角相等，正确，是真命题；
②在同一平面内，垂直于同一条直线的两直线平行，正确，是真命题；
③相等的角是对顶角，错误，是假命题，反例“角平分线分成的两个角相等”，但它们不是对顶角；
由“两直线平行，同位角相等”，前提是两直线平行，故④是假命题；
故选：C．
【点睛】
本题考查了命题与定理，解题的关键是了解对顶角的性质、平行线的性质等基础知识．
7、D
【分析】
利用互为相反数的两个数的平方也相等，有理数的大小比较，同位角和对顶角的概念性质进行分析判断即可．
【详解】
解：A、若，则或，故A错误．
B、当时，有，故B错误．
C、两直线平行，同位角相等，故C错误．
D、对顶角相等，D正确．
故选：D ．
【点睛】
本题主要是考查了平方、绝对值的比较大小、同位角和对顶角的性质，熟练掌握相关概念及性质，是解决本题的关键．
8、B
【分析】
先证明DEBC，根据平行线的性质求解．
【详解】
解：因为∠B＝∠ADE＝70°
所以DEBC，
所以∠DEC+∠C＝180°，所以∠C＝80°.
故选：B．
【点睛】
此题主要考查平行线的判定与性质，解题的关键是熟知同位角相等，两直线平行．
9、C
【分析】
根据互补即两角的和为180°，互余的两角和为90°，设这个角为x，即可求出答案．
【详解】
解：设这个角为x，则这个角的补角为180°-x，这个角的补角为90°-x，
根据题意得：180°-x-（90°-x）=90°，
故选：C．
【点睛】
本题主要考查了余角和补角的概念与性质．互为余角的两角的和为90°，互为补角的两角之和为180°．
10、D
【分析】
根据题意画图如图（1），根据平行线性质两直线平行，同位角相等，即可得出∠α＝∠1＝∠β，即可得出答案，如图（2）根据平行线性质，两直线平行，同旁内角互补，∠α+∠2＝180°，再根据两直线平行，内错角相等，∠2＝∠β，即可得出答案．
【详解】
解：如图1，
∵a∥b，
∴∠1＝∠α，
∵c∥d，
∴∠β＝∠1＝∠α＝60°；
如图（2），
∵a∥b，
∴∠α+∠2＝180°，
∵c∥d，
∴∠2＝∠β，
∴∠β+∠α＝180°，
∵∠α＝60°，
∴∠β＝120°．
综上，∠β＝60°或120°．
故选：D．
【点睛】
本题主要考查了平行线的性质，熟练掌握相关性质进行计算是解决本题的关键．
二、填空题
1、平行
【分析】
过点作，根据两直线平行，同旁内角互补，从而出，即可得出结果．
【详解】
解：过点作，
∴，
∵∠BAC+∠ACE+∠CEF＝360°，
∴，
∴，
∴,
故答案为：平行．
【点睛】
本题考查了平行线的判定与性质以及平行线的推论，根据题意作出合理的辅助线是解本题的关键．
2、33°
【分析】
由题意直接根据∠2＝180°﹣∠COE﹣∠1，进行计算即可得出答案．
【详解】
解：由题意得：∠2＝180°﹣∠COE﹣∠1＝180°﹣90°﹣57°＝33°．
故答案为：33°．
【点睛】
本题考查余角和补角的知识，属于基础题，注意数形结合思维分析的运用．
3、123°27′
【分析】
本题考查互补和互余的概念，和为180度的两个角互为补角；和为90度的两个角互为余角．
【详解】
解：∠1与∠2互余，且∠1=∠1=33°27′，
则∠2=90°-33°27′=56°33′，
∠2的补角的度数为180°-56°33′=123°27′．
故答案为：123°27′．
【点睛】
本题考查的是余角和补角的概念，如果两个角的和等于90°，就说这两个角互为余角；如果两个角的和等于180°，就说这两个角互为补角．
4、20
【分析】
利用角平分线的定义求解再由可得再列方程求解即可.
【详解】
解： BD平分，，

由，
而，

解得：
所以当时，，
故答案为：
【点睛】
本题考查的是角平分线的定义，平行线的判定与性质，一元一次方程的应用，掌握平行线的判定与性质是解本题的关键.
5、②③④
【分析】
根据平行线的判定定理，逐一判断，即可得到答案．
【详解】
∵，
∴，
∴①不符合题意；
∵∠C+∠ABC=180°，
∴AB∥CD；
∴②符合题意；
∵∠A=∠CDE，
∴AB∥CD；
∴③符合题意；
∵∠1=∠2，
∴AB∥CD．
故答案为：②③④．
【点睛】
本题主要考查平行线的判定定理，掌握平行线的判定定理是解题的关键．平行线的判定：内错角相等，两直线平行；同位角相等，两直线平行；同旁内角互补，两直线平行．
三、解答题
1、（1）；（2）∠ABC的度数改变，度数为．
【解析】
【分析】
（1）过点E作，根据平行线性质推出∠ABE=∠BEF，∠CDE=∠DEF，根据角平分线定义得出，∠CDE=∠ADC=35°，求出∠BEF的度数，进而可求出∠ABC的度数；
（2）过点E作，根据角平分线定义得出，∠CDE=∠ADC=35°，求出∠BEF的度数，进而可求出∠ABC的度数．
【详解】
（1）如图1，过点作．
∵，
∴，
∴．
∵平分平分，，
∴．
∵，
∴，
∴．
（2）的度数改变．
画出的图形如图2，过点作．
∵平分，平分，，
∴ ．
∵，
∴，
∴．
∵，
∴，
∴，
∴．
【点睛】
本题考查了平行线性质和角平分线定义的应用，主要考查学生的推理能力．熟练掌握平行线的判定与性质是解答本题的关键．
2、（1）140゜（2）存在，t=2秒或20秒；（3）秒
【解析】
【分析】
（1）设∠COE=x度，则其补角为(180−x)度，根据∠COE比它的补角大100°列方程即可求得结果；
（2）存在两种情况：当OC在直线DE上方时；当OC在直线DE下方时；就这两种情况考虑即可；
（3）画出图形，结合图形表示出∠COE与∠COB，根据角平分线的性质建立方程即可求得t值．
【详解】
（1）设∠COE=x度，则其补角为(180−x)度，由题意得：x−(180−x)=100
解得：x=140
即∠COE=140゜
（2）存在
当OC在直线DE上方时，此时OB平分∠BOC
∵∠COE=140゜
∴
当OB没有旋转时，∠BOC=50゜
所以OB旋转了70゜−50゜=20゜
则旋转的时间为：t=20÷10=2（秒）
当OC在直线DE下方时，如图
由图知：∠BOE+∠BOC+∠COE=360゜即：2∠BOE+∠COE=360゜
∵OB旋转了10t度
∴∠BOE=(10t−90)度
∴2(10t−90)+140=360
解得：t=20
综上所述，当t=2秒或20秒时，∠BOC=∠BOE
（3）OB、OC同时旋转10t度
如图所示，∠COE=(180゜+40゜)−(10t)゜=(220−10t)゜
∵2×(10t)゜−∠COB+50゜=360゜
∴∠COB=2× (10t)゜−310゜
∵∠COB=∠COE
∴2× 10t−310=220-10t
解得：
即当t的值为秒时，满足条件．
【点睛】
本题考查了角平分线的性质，角的和差运算，补角的概念，解一元一次方程等知识，注意数形结合及分类讨论．
3、垂直的定义；同位角相等，两直线平行；两直线平行，同位角相等；BAD；两直线平行，同旁内角互补
【解析】
【分析】
先由垂直的定义得出两个90°的同位角，根据同位角相等判定两直线平行，根据两直线平行，同位角相等得到，再根据等量代换得出，根据内错角相等，两直线平行，最后根据两直线平行，同旁内角互补即可判定．
【详解】
解：∵AD⊥BC，EF⊥BC（已知），
∴∠EFB＝90°，∠ADB＝90°（垂直的定义），
∴∠EFB＝∠ADB（等量代换），
∴EFAD（同位角相等，两直线平行），
∴∠1＝∠BAD（两直线平行，同位角相等），
又∵∠1＝∠2（已知），
∴∠2＝∠BAD（等量代换），
∴DGBA（内错角相等，两直线平行），
∴∠BAC+∠AGD＝180°（两直线平行，同旁内角互补）．
故答案为：垂直的定义；同位角相等，两直线平行；两直线平行，同位角相等；BAD；两直线平行，同旁内角互补
【点睛】
本题考查的是平行线的性质及判定，熟练掌握平行线的性质定理和判定定理是关键．
4、（1）；（2）
【解析】
【分析】
（1）根据角平分线的定义，平角的定义求解即可；
（2）根据角平分线的定义，互补和互余的意义计算即可得出答案．
【详解】
解：（1）如图，∵是的平分线，
∴.
∵是的平分线，
∴.
∴．
（2）由（1）可知.
∴.
【点睛】
本题考查角平分线的定义、平角的定义，互余、互补的意义以及角的和差关系，通过图形直观得出各个角之间的关系式正确解答的关键．
5、（1）78°；（2）80°．
【解析】
【分析】
（1）根据角平分线的定义（从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线）结合图形可得，然后将角度代入计算即可；
（2）由互补可得，结合图形可得：，，由角平分线定义（从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线）可得，利用等量代换得出，将已知角度代入求解即可．
【详解】
解：（1）OB是的平分线，且，
OD是的平分线，且，
∴，
，
∴，
∴；
（2）∵与互补，
∴，
由图知：，
，
由角平分线定义知：，
∴，
即，
∵，
∴，
即．
【点睛】
题目主要考查角平分线及互补的定义，角度之间的计算，理解题意，找准角度进行计算是解题关键．