初中北京课改版第七章 观察、猜想与证明综合与测试同步达标检测题

这是一份初中北京课改版第七章 观察、猜想与证明综合与测试同步达标检测题，共21页。试卷主要包含了如图，能判定AB∥CD的条件是等内容，欢迎下载使用。
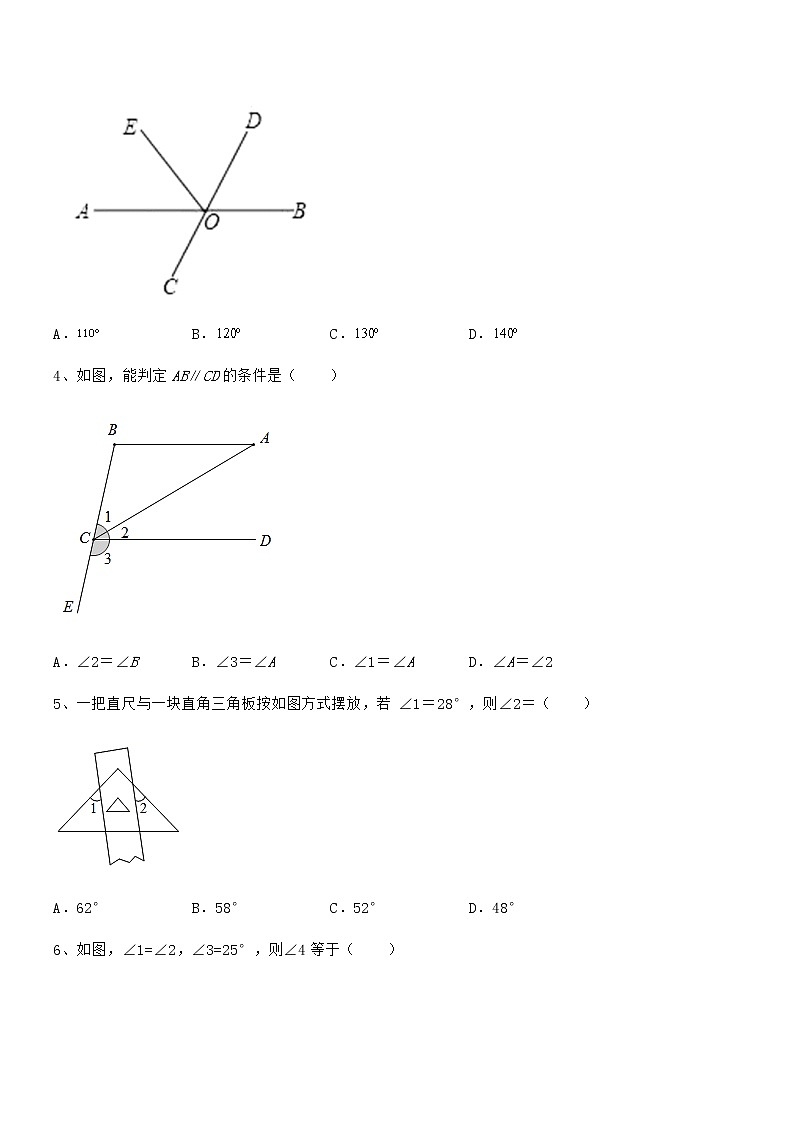
京改版七年级数学下册第七章观察、猜想与证明难点解析 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，下列给定的条件中，不能判定的是（　　）A． B． C． D．2、若的补角是150°，则的余角是（    ）A．30° B．60° C．120° D．150°3、如图，已知直线，相交于O，平分，，则的度数是（    ）A． B． C． D．4、如图，能判定AB∥CD的条件是（    ）A．∠2＝∠B B．∠3＝∠A C．∠1＝∠A D．∠A＝∠25、一把直尺与一块直角三角板按如图方式摆放，若∠1＝28°，则∠2＝（　　）A．62° B．58° C．52° D．48°6、如图，∠1=∠2，∠3=25°，则∠4等于（    ）A．165° B．155° C．145° D．135°7、如图，一副三角尺按不同的位置摆放，下列摆放方式中与相等的是（    ）．A． B．C． D．8、如图，一条公路经过两次转弯后又回到原来的方向，如果第一次的拐角为150°，则第二次的拐角为（　　）A．40° B．50° C．140° D．150°9、如果一个角的补角是这个角的4倍，那么这个角为（　　）A．36° B．30° C．144° D．150°10、如图，一辆快艇从P处出发向正北航行到A处时向左转50°航行到B处，再向右转80°继续航行，此时航行方向为（　　）
A．西偏北50° B．北偏西50° C．东偏北30° D．北偏东30°第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，AD是∠EAC的平分线，AD∥BC，∠B＝40°，则∠DAC的度数为____．2、已知∠A=38°24'，则∠A的补角的大小是____．3、如图，∠1还可以用______ 表示，若∠1=62°，那么∠BCA=____ 度．4、将一张长方形纸片按如图所示折叠，如果∠1＝65°，那么∠2等于_____．5、若α＝25°57′，则2α的余角等于_____．三、解答题（5小题，每小题10分，共计50分）1、如图所示，AB//CD，点E为两条平行线外部一点，F为两条平行线内部一点，G、H分别为AB、CD上两点，GB平分∠EGF，HF平分∠EHD，且2∠F与∠E互补，求∠EGF的大小．2、填空，完成下列说理过程：如图，直线EF和CD相交于点O，∠AOB＝90°，OC平分∠AOF，∠AOE＝40°．求∠BOD的度数．解：∵∠AOE＝40°（已知）∴∠AOF＝180°﹣         （邻补角定义）＝180°﹣         °＝         °∵OC平分∠AOF（已知）∴∠AOC∠AOF（         ）∵∠AOB＝90°（已知）∴∠BOD＝180°﹣∠AOB﹣∠AOC（         ）＝180°﹣90°﹣         °＝         °3、如图，如果∠1＝60°，∠2＝120°，∠D＝60°，那么AB与CD平行吗？BC与DE呢？观察下面的解答过程，补充必要的依据或结论．解∵∠1＝60°（已知）∠ABC＝∠1 （①　 　）∴∠ABC＝60°（等量代换）又∵∠2＝120°（已知）∴（②　   　）+∠2＝180°（等式的性质）∴AB∥CD （③　   　）又∵∠2+∠BCD＝（④　 　°）∴∠BCD＝60°（等式的性质）∵∠D＝60°（已知）∴∠BCD＝∠D （⑤　   　）∴BC∥DE （⑥　   　）4、如图，在下列解答中，填写适当的理由或数学式：   （1）∵∠A=∠CEF，（ 已知 ）   ∴________∥________；  （________）（2）∵∠B+∠BDE=180°，（ 已知 ）   ∴________∥________；（________） （3）∵DE∥BC，（ 已知 ）   ∴∠AED=∠________； （________）（4）∵AB∥EF，（ 已知 ）   ∴∠ADE=∠________．（________）5、完成下面的证明．如图，已知AD⊥BC，EF⊥BC，∠1＝∠2，求证：∠BAC+∠AGD＝180°．证明：∵AD⊥BC，EF⊥BC（已知），∴∠EFB＝90°，∠ADB＝90°（      ），∴∠EFB＝∠ADB（等量代换），∴EFAD（      ），∴∠1＝∠BAD（      ），又∵∠1＝∠2（已知），∴∠2＝∠   （等量代换），∴DGBA（内错角相等，两直线平行），∴∠BAC+∠AGD＝180°（      ）． ---------参考答案-----------一、单选题1、A【分析】根据平行线的判定条件：同位角相等，两直线平行，同旁内角互补，两直线平行，内错角相等，两直线平行，进行逐一判断即可．【详解】解：A选项：当∠1=∠A时，可知是DE和AC被AB所截得到的同位角，可得到DE∥AC，而不是AB∥DF，故符合题意；B选项：当∠A=∠3时，可知是AB、DF被AC所截得到的同位角，可得AB∥DF，故不符合题意；C选项：当∠1=∠4时，可知是AB、DF被DE所截得到的内错角，可得AB∥DF，故不符合题意；D选项：当∠2+∠A=180°时，是一对同旁内角，可得AB∥DF；故不符合题意；故选A．【点睛】本题主要考查了平行线的判定，熟知平行线的判定条件是解题的关键．2、B【分析】根据补角、余角的定义即可求解．【详解】∵的补角是150°∴=180°-150°=30°∴的余角是90°-30°=60°故选B．【点睛】此题主要考查余角、补角的求解，解题的关键是熟知如果两个角的和为90度，这两个角就互为余角；补角是指如果两个角的和是一个平角，那么这两个角叫互为补角，其中一个角叫做另一个角的补角3、C【分析】先根据角平分线的定义求得∠AOC的度数，再根据邻补角求得∠BOC的度数即可．【详解】解：∵OA平分∠EOC，∠EOC＝100°，∴∠AOC＝∠EOC＝50°，∴∠BOC＝180°﹣∠AOC＝130°．故选：C．【点睛】本题考查角平分线的有关计算，邻补角．能正确识图是解题关键．4、D【分析】根据平行线的判定定理，找出正确选项即可.【详解】根据内错角相等，两直线平行，∵∠A＝∠2，∴AB∥CD，故选：D.【点睛】本题主要考查了平行线的判定，解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角，培养了学生“执果索因”的思维方式与能力．5、A【分析】过三角板的直角顶点作直尺两边的平行线，根据平行线的性质（两直线平行，同位角相等）即可求解．【详解】解：如图，过三角板的直角顶点作直尺两边的平行线，∵直尺的两边互相平行，∴，∴，∴，故选：A．【点睛】本题考查平行线的性质，掌握平行线的性质是解题的关键．6、B【分析】设∠4的补角为，利用∠1=∠2求证，进而得到，最后即可求出∠4．【详解】解：设∠4的补角为，如下图所示：
 ∠1=∠2，，，．故选：B．【点睛】本题主要是考查了平行线的性质与判定，熟练角相等，证明两直线平行，然后利用平行关系证明其他角相等，这是解决该题的关键．7、C【分析】根据同角的余角相等，补角定义，和平角的定义、三角形内角和对各小题分析判断即可得解．【详解】解：A、＋＝180°−90°＝90°，互余；B、＋＝60°+30°+45°＝135°；C、根据同角的余角相等，可得＝；D、＋＝180°，互补；故选：C．【点睛】本题考查了余角和补角、三角形内角和，是基础题，熟记概念与性质是解题的关键．8、D【分析】由于拐弯前、后的两条路平行，可考虑用平行线的性质解答．【详解】解：∵拐弯前、后的两条路平行，∴∠B=∠C=150°（两直线平行，内错角相等）．
故选：D．【点睛】本题考查平行线的性质，解答此题的关键是将实际问题转化为几何问题，利用平行线的性质求解．9、A【分析】设这个角为 ，则它的补角为 ，根据“一个角的补角是这个角的4倍”，列出方程，即可求解．【详解】解：设这个角为 ，则它的补角为 ，根据题意得： ，解得： ．故选：A【点睛】本题主要考查了补角的性质，一元一次方程的应用，明确题意，准确得到等量关系是解题的关键．10、D【分析】由，证明，再利用角的和差求解 从而可得答案.【详解】解：如图，标注字母， ，
 ∴, 此时的航行方向为北偏东30°， 故选：D．【点睛】本题考查的是平行线的性质，角的和差运算，掌握“两直线平行，同位角相等”是解本题的关键.二、填空题1、40°【分析】根据平行线的性质可得∠EAD=∠B，根据角平分线的定义可得∠DAC=∠EAD，即可得答案．【详解】∵AD∥BC，∠B＝40°，∴∠EAD=∠B=40°，∵AD是∠EAC的平分线，∴∠DAC=∠EAD=40°，故答案为：40°【点睛】本题考查平行线的性质及角平分线的定义，两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；熟练掌握平行线的性质是解题关键．2、141°36′【分析】根据补角的定义即可求解．【详解】解：∠A的补角 =180°- 38°24'= 141°36′ ．故答案为：141°36′【点睛】本题考查了补角的定义，熟知补角的定义“如果两个角的和是180°，则这两个角互为补角”是解题关键．3、        【分析】根据角的表示和邻补角的性质计算即可；【详解】∠1还可以用表示；∵∠1=62°，，∴；故答案是：；．【点睛】本题主要考查了角的表示和邻补角的性质，准确计算是解题的关键．4、50°【分析】根据平行线的性质计算即可；【详解】解：如图所示，由折叠可得，∠3＝∠1＝65°，∴∠CEG＝130°，∵AB∥CD，∴∠2＝180°﹣∠CEG＝180°﹣130°＝50°．故答案为：50°．【点睛】本题主要考查了平行线的性质应用，准确计算是解题的关键．5、38°6′【分析】根据余角的和等于90°列式计算即可求解．【详解】解：∵α＝25°57′，∴2α＝51°54′，∴2α的余角＝90°﹣51°54′＝38°6′．故答案为：38°6′．【点睛】此题主要考查角度的计算，解题的关键是熟知余角的性质．三、解答题1、∠EGF=120°．【解析】【分析】过点F作FM∥AB，设AB于EH的交点为N，先设，则，由题意及平行线的性质得，，得到，，由于与互补，得到，最终问题可求解【详解】解：过点F作FM∥AB，设AB于EH的交点为N，如图所示：设，∵GB平分∠EGF，HF平分∠EHD，∴，∵AB//CD，∴FM∥AB∥CD，∴，∴，，即，，∵与互补，∴，∴，∴，∴．【点睛】本题考查平行线的性质及三角形外角的性质，解题的关键是设，且由题意得到x，y的关系．2、角平分线的定义，平角的定义，【解析】【分析】先利用邻补角的含义求解 再利用角平分线的含义证明：∠AOC∠AOF，再利用平角的定义结合角的和差关系可得答案.【详解】解：∵∠AOE＝40°（已知）∴∠AOF＝180°﹣（邻补角定义）＝180°﹣40°＝140°∵OC平分∠AOF（已知）∴∠AOC∠AOF（角平分线的定义）∵∠AOB＝90°（已知）∴∠BOD＝180°﹣∠AOB﹣∠AOC（平角的定义）＝180°﹣90°﹣70°＝20°故答案为：角平分线的定义，平角的定义，【点睛】本题考查的是平角的定义，邻补角的含义，角平分线的定义，角的和差运算，掌握“几何图形中角的和差关系”是解本题的关键.3、对顶角相等；∠ABC；同旁内角互补，两直线平行；180；等量代换；内错角相等，两直线平行．【解析】【分析】先求出∠ABC＝60°，即可证明∠ABC+∠2＝180°得到AB∥CD，然后求出∠BCD＝∠D 即可证明BC∥DE．【详解】解∵∠1＝60°（已知）∠ABC＝∠1 （对顶角相等），∴∠ABC＝60°（等量代换），又∵∠2＝120°（已知），∴∠ABC+∠2＝180°（等式的性质），∴AB∥CD （同旁内角互补，两直线平行），又∵∠2+∠BCD＝180°，∴∠BCD＝60°（等式的性质），∵∠D＝60°（已知），∴∠BCD＝∠D （等量代换），∴BC∥DE （内错角相等，两直线平行），故答案为：对顶角相等；∠ABC；同旁内角互补，两直线平行；180；等量代换；内错角相等，两直线平行．【点睛】本题主要考查了平行线的判定，对顶角相等，解题的关键在于能够熟练掌握平行线的判定条件．4、（1）AB；EF；同位角相等，两直线平行；（2）DE；BC；同旁内角互补，两直线平行；（3）C；两直线平行，同位角相等；（4）DEF；两直线平行，内错角相等【解析】【分析】（1）根据平行线的判定定理：同位角相等，两直线平行，即可得；（2）根据平行线的判定定理：同旁内角互补，两直线平行，即可得；（3）根据平行线的性质：两直线平行，同位角相等，即可得；（4）根据平行线的性质：两直线平行，内错角相等，即可得．【详解】解：（1）∵，（已知）∴，（同位角相等，两直线平行）；（2）∵，（已知）∴，（同旁内角互补，两直线平行）；（3）∵，（已知）∴，（两直线平行，同位角相等）（4）∵，（已知）∴（两直线平行，内错角相等）．故答案为：（1）AB；EF；同位角相等，两直线平行；（2）DE；BC；同旁内角互补，两直线平行；（3）C；两直线平行，同位角相等；（4）DEF；两直线平行，内错角相等．【点睛】题目主要考查平行线的判定定理和性质，熟练掌握理解平行线的性质定理并结合图形是解题关键．5、垂直的定义；同位角相等，两直线平行；两直线平行，同位角相等；BAD；两直线平行，同旁内角互补【解析】【分析】先由垂直的定义得出两个90°的同位角，根据同位角相等判定两直线平行，根据两直线平行，同位角相等得到，再根据等量代换得出，根据内错角相等，两直线平行，最后根据两直线平行，同旁内角互补即可判定．【详解】解：∵AD⊥BC，EF⊥BC（已知），∴∠EFB＝90°，∠ADB＝90°（垂直的定义），∴∠EFB＝∠ADB（等量代换），∴EFAD（同位角相等，两直线平行），∴∠1＝∠BAD（两直线平行，同位角相等），又∵∠1＝∠2（已知），∴∠2＝∠BAD（等量代换），∴DGBA（内错角相等，两直线平行），∴∠BAC+∠AGD＝180°（两直线平行，同旁内角互补）．故答案为：垂直的定义；同位角相等，两直线平行；两直线平行，同位角相等；BAD；两直线平行，同旁内角互补【点睛】本题考查的是平行线的性质及判定，熟练掌握平行线的性质定理和判定定理是关键．