2021学年第七章 观察、猜想与证明综合与测试精练

京改版七年级数学下册第七章观察、猜想与证明综合练习

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

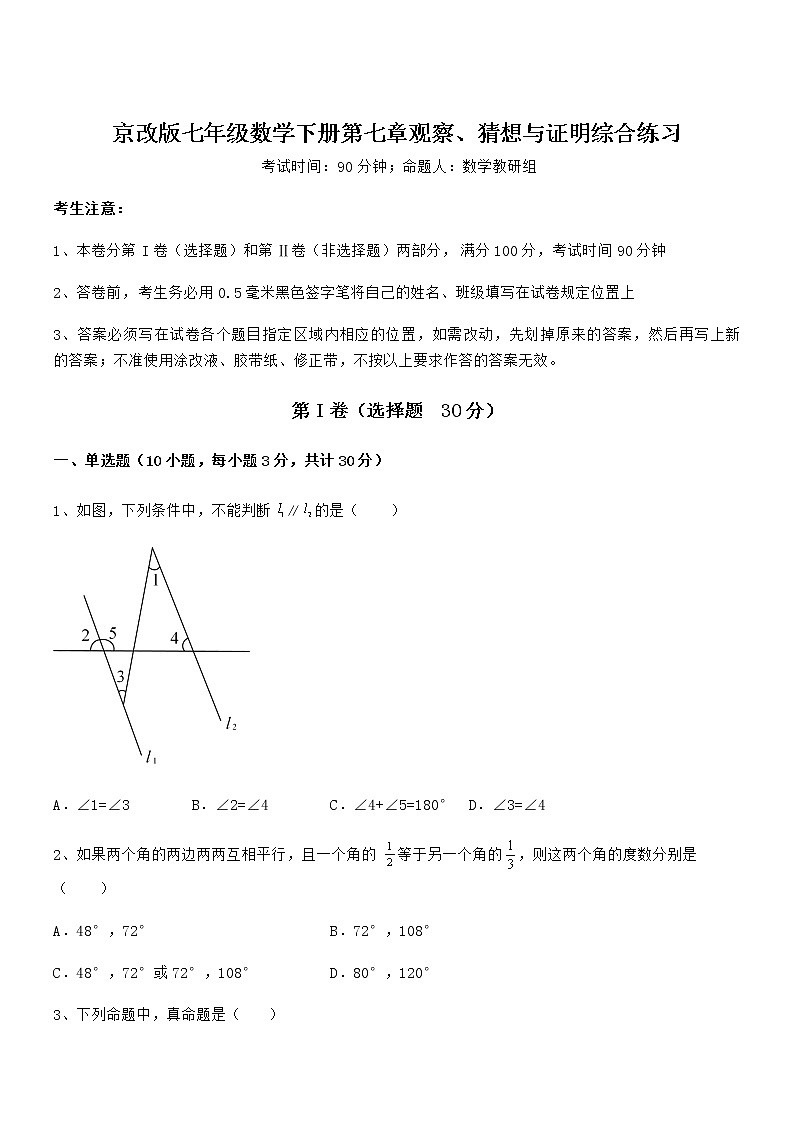
1、如图，下列条件中，不能判断∥的是（    ）

A．∠1=∠3 B．∠2=∠4 C．∠4+∠5=180° D．∠3=∠4

2、如果两个角的两边两两互相平行，且一个角的等于另一个角的，则这两个角的度数分别是（　　）

A．48°，72° B．72°，108°

C．48°，72°或72°，108° D．80°，120°

3、下列命题中，真命题是（   ）

A．两条直线被第三条直线所截，内错角相等 B．相等的角是对顶角

C．在同一平面内，垂直于同一条直线的两条直线平行 D．同旁内角互补

4、在证明命题“若，则”是假命题时，下列选项中所举反例不正确的是（    ）

A． B． C． D．

5、下列语句中，错误的个数是（    ）

①直线AB和直线BA是两条直线；

②如果，那么点C是线段AB的中点；

③两点之间，线段最短；

④一个角的余角比这个角的补角小．

A．1个 B．2个 C．3个 D．4个

6、如图，若要使与平行，则绕点至少旋转的度数是（    ）

A． B． C． D．

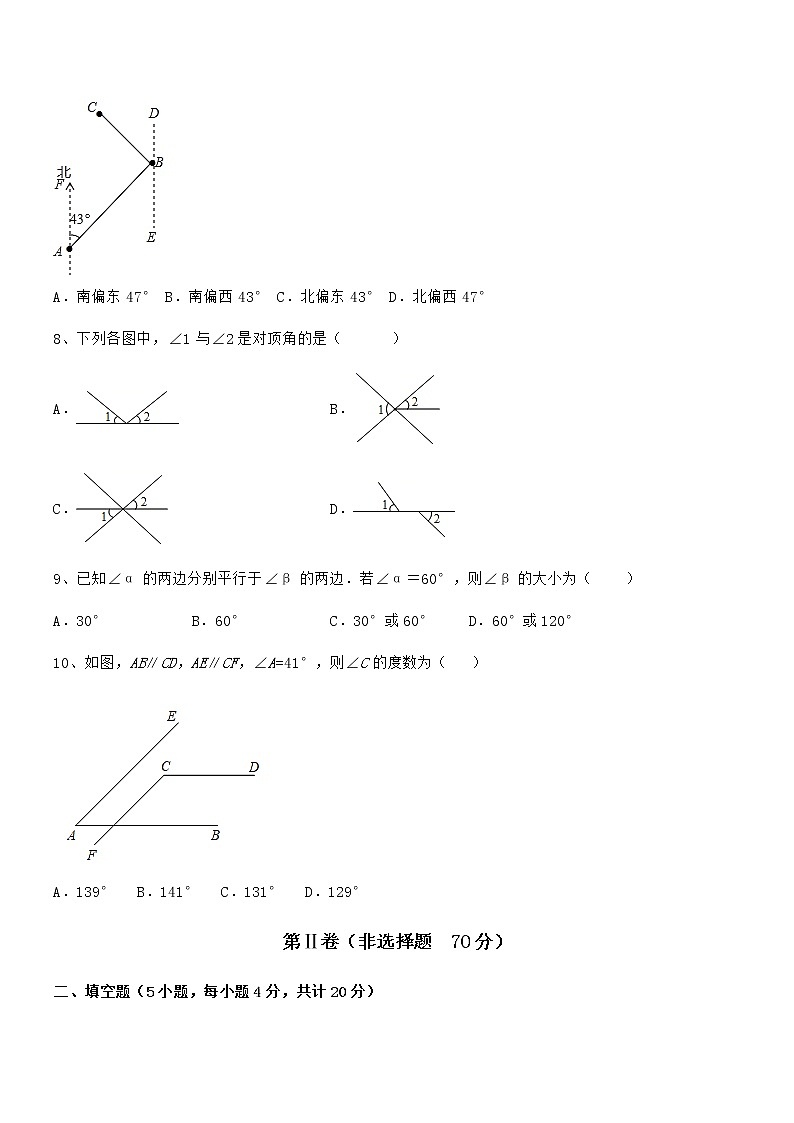
7、如图，有A，B，C三个地点，且∠ABC＝90°，B地在A地的北偏东43°方向，那么C地在B地的（　　）方向．

A．南偏东47° B．南偏西43° C．北偏东43° D．北偏西47°

8、下列各图中，∠1与∠2是对顶角的是（      ）

A．  B． 

C．  D．

9、已知∠α的两边分别平行于∠β的两边．若∠α＝60°，则∠β的大小为（　　）

A．30° B．60° C．30°或60° D．60°或120°

10、如图，AB∥CD，AE∥CF，∠A=41°，则∠C的度数为（   ）

A．139° B．141° C．131° D．129°

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、如图所示，过点P画直线a的平行线b的作法的依据是___________．

2、已知∠α与∠β互余，且∠α=40°，则∠β的度数为________．

3、一副三角板按如图方式放置，含45°角的三角板的斜边与含30°角的三角板的长直角边平行，则∠α的度数是______．

4、已知一个角的补角是这个角的余角的3倍，则这个角是______度．

5、如图所示，，点B，O，D在同一直线上，若，则的度数为______．

三、解答题（5小题，每小题10分，共计50分）

1、如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°，

（1）请判断AB与CD的位置关系并说明理由；

（2）如图2，当∠E=90°且AB与CD的位置关系保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD是否存在确定的数量关系？并说明理由；

（3）如图3，P为线段AC上一定点，点Q为直线CD上一动点且AB与CD的位置关系保持不变，当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．

2、已知，与互余，OP是的角平分线．

（1）画出所有符合条件的图形．

（2）计算的度数．

3、如图，已知∠AOB＝140°，∠COE与∠EOD互余，OE平分∠AOD．

（1）若∠COE＝40°，求∠DOE和∠BOD；

（2）设∠COE＝α，∠BOD＝β，试探究α与β之间的数量关系．

4、如图，直线AB，CD，EF相交于点O，OG⊥CD．

（1）已知∠AOC＝38°12'，求∠BOG的度数；

（2）如果OC是∠AOE的平分线，那么OG是∠EOB的平分线吗？说明理由．

5、已知：锐角∠AOB．

（1）若∠AOB=65°，则∠AOB的余角的度数为________度．

（2）若∠AOB=53°17ʹ，则∠AOB的补角的度数为________．

（3）若∠AOB=31°12ʹ，计算：∠AOB=___________．

（4）若∠AOB=20°21ʹ，计算：3∠AOB．

---------参考答案-----------

一、单选题

1、D

【分析】

根据平行线的判定定理对各选项进行逐一判断即可．

【详解】

解：、，内错角相等，

，故本选项错误，不符合题意；

、，同位角相等，

，故本选项错误，不符合题意；

、，同旁内角互补，

，故本选项错误，不符合题意；

、，它们不是内错角或同位角，

与的关系无法判定，故本选项正确，符合题意．

故选：D．

【点睛】

本题考查的是平行线的判定，解题的关键是熟知同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行的知识．

2、B

【分析】

根据题意可得这两个角互补，设其中一个角为x，则另一个角为，由两个角之间的数量关系列出一元一次方程，求解即可得．

【详解】

解：∵两个角的两边两两互相平行，

∴这两个角可能相等或者两个角互补，

∵一个角的等于另一个角的，

∴这两个角互补，

设其中一个角为x，则另一个角为，

根据题意可得：，

解得：，，

故选：B．

【点睛】

题目主要考查平行线的性质、角的数量关系、一元一次方程等，理解题意，列出方程是解题关键．

3、C

【分析】

分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．

【详解】

解：A、错误，当被截的直线平行时形成的同位角才相等；

B、错误，对顶角相等但相等的角不一定是对顶角；

C、正确，必须强调在同一平面内；

D、错误，两直线平行同旁内角才互补．

故选：C．

【点睛】

主要考查命题的真假判断与平行线的性质、对顶角的特点，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．

4、A

【分析】

所谓举反例是指满足命题的条件但不满足命题的结论，由此可判断．

【详解】

显然A选项既满足命题的条件也满足命题的结论，故不是举反例，其它三个选项满足命题的条件，但不满足命题的结论，所以都是举反例；

故选：A

【点睛】

本题考查了命题的真假，说明一个命题是假命题要举反例．掌握举反例的含义是关键．

5、B

【分析】

根据直线的定义、线段中点的定义、线段的性质、余角与补角的定义分别判断．

【详解】

解：①直线AB和直线BA是同一条直线，故该项符合题意；

②如果，那么点C不一定是线段AB的中点，故该项符合题意；

③两点之间，线段最短，故该项不符合题意；

④一个角的余角比这个角的补角小，故该项不符合题意，

故选：B．

【点睛】

此题考查了直线的定义、线段中点的定义、线段的性质、余角与补角的定义，属于基础定义题型．

6、A

【分析】

根据“两直线平行，内错角相等”进行计算．

【详解】

解：如图，

∵l1∥l2，

∴∠AOB=∠OBC=42°，

∴80°-42°=38°，

即l1绕点O至少旋转38度才能与l2平行．

故选：A．

【点睛】

考查了旋转的性质和平行线的性质，根据平行线的性质得到∠AOB=∠OBC=42°是解题的关键，难度不大．

7、D

【分析】

根据方向角的概念，和平行线的性质求解．

【详解】

解：如图：

∵AF∥DE，

∴∠ABE＝∠FAB＝43°，

∵AB⊥BC，

∴∠ABC＝90°，

∴∠CBD＝180°﹣90°﹣43°＝47°，

∴C地在B地的北偏西47°的方向上．

故选：D．

【点睛】

本题主要考查了方位角，平行线的性质，正确的识别图形是解题的关键．

8、C

【分析】

根据对顶角的定义作出判断即可．

【详解】

解：根据对顶角的定义可知：只有C选项的是对顶角，其它都不是．
故选C．

【点睛】

本题考查对顶角的定义，两条直线相交后所得的只有一个公共顶点且两边互为反向延长线，这样的两个角叫做对顶角．

9、D

【分析】

根据题意画图如图（1），根据平行线性质两直线平行，同位角相等，即可得出∠α＝∠1＝∠β，即可得出答案，如图（2）根据平行线性质，两直线平行，同旁内角互补，∠α+∠2＝180°，再根据两直线平行，内错角相等，∠2＝∠β，即可得出答案．

【详解】

解：如图1，

∵a∥b，

∴∠1＝∠α，

∵c∥d，

∴∠β＝∠1＝∠α＝60°；

如图（2），

∵a∥b，

∴∠α+∠2＝180°，

∵c∥d，

∴∠2＝∠β，

∴∠β+∠α＝180°，

∵∠α＝60°，

∴∠β＝120°．

综上，∠β＝60°或120°．

故选：D．

【点睛】

本题主要考查了平行线的性质，熟练掌握相关性质进行计算是解决本题的关键．

10、A

【分析】

如图，根据AECF，得到∠CGB=41°，根据ABCD，即可得到∠C=139°．．

【详解】

解：如图，∵AECF，

∴∠A=∠CGB=41°，

∵ABCD，

∴∠C=180°-∠CGB=139°．

故选：A

【点睛】

本题考查了平行线的性质，熟知平行线的性质是解题关键．

二、填空题

1、内错角相等，两直线平行

【分析】

根据平行线的判定方法解决问题即可．

【详解】

解：由作图可知，

，

（内错角相等两直线平行），

故答案为：内错角相等，两直线平行．

【点睛】

本题考查作图，平行线的判定等知识，熟练掌握平行线的判定定理是解题的关键，属于中考常考题型．

2、50°

【分析】

根据两个角互余，则两个角相加之和为90°，进行求解即可．

【详解】

解:∵∠α与∠β互余，且∠α＝40°，

∴∠β=90°-∠α=50°，

故答案为：50°．

【点睛】

本题考查了求一个角的余角，熟知两个角互余则它们之和等于90°是解答本题的关键．

3、15°

【分析】

根据平行线的性质和三角板的特殊角的度数解答即可．

【详解】

解：如图：

∵ABCD，

∴∠BAD＝∠D＝30°，

∵∠BAE＝45°，

∴∠α＝45°﹣30°＝15°，

故答案为：15°．

【点睛】

此题主要考查平行线的性质，解题的关键是熟知两直线平行，内错角相等．

4、

【分析】

设这个角为 则这个角的补角为： 这个角的余角为： 根据等量关系一个角的补角是这个角的余角的3倍，列方程，解方程可得．

【详解】

解：设这个角为 则这个角的补角为： 这个角的余角为：

，

，

，

，

答：这个角为．

故答案为：．

【点睛】

本题考查的是余角与补角的含义，一元一次方程的应用，掌握以上知识是解题的关键．

5、116°

【分析】

由图示可得，∠1与∠BOC互余，结合已知可求∠BOC，又因为∠2与∠COB互补，即可求出∠2的度数．

【详解】

解：∵，∠AOC＝90°，

∴∠BOC＝64°，

∵∠2＋∠BOC＝180°，

∴∠2＝116°．

故答案为：116°．

【点睛】

此题考查了余角和补角的知识，属于基础题，关键是掌握互余的两角之和为90°，互补的两角之和为180°．

三、解答题

1、（1）平行，理由见解析；（2）∠BAE+∠MCD=90°，理由见解析；（3）∠BAC=∠PQC+∠QPC，理由见解析．

【解析】

【分析】

（1）先根据CE平分∠ACD，AE平分∠BAC可得∠BAC=2∠EAC，∠ACD=2∠ACE，再由∠EAC+∠ACE=90°可知∠BAC+∠ACD=180，根据平行线的判定定理即可得出结论；

（2）如图，过E作EF∥AB，由AB//CD可得EF∥AB∥CD，根据平行线的性质可得∠BAE=∠AEF，∠FEC=∠DCE，可得∠BAE+∠ECD=90°，再由∠MCE=∠ECD即可得出结论；

（3）如图，过点C作CM//PQ，可得∠PQC=∠MCN，∠QPC=∠PCM，根据AB∥CD可知∠BAC+∠ACD=180°，根据∠PCQ+∠PCM+∠MCN=180°，可得∠QPC+∠PQC+∠PCQ=180°，即可得出∠BAC=∠PQC+∠QPC．

【详解】

（1）∵CE平分∠ACD，AE平分∠BAC，

∴∠BAC=2∠EAC，∠ACD=2∠ACE，

∵∠EAC+∠ACE=90°，

∴∠BAC+∠ACD=180°，

∴AB∥CD

（2）∠BAE+∠MCD=90°；理由如下：

如图，过E作EF∥AB，

∵AB∥CD，

∴EF∥AB∥CD，

∴∠BAE=∠AEF，∠FEC=∠DCE，

∵∠AEC=∠AEF+∠FEC=90°，

∴∠BAE+∠ECD=90°，

∵∠MCE=∠ECD=∠MCD，

∴∠BAE+∠MCD=90°．

（3）如图，过点C作CM//PQ，

∴∠PQC=∠MCN，∠QPC=∠PCM，

∵AB∥CD，

∴∠BAC+∠ACD=180°，

∵∠PCQ+∠PCM+∠MCN=180°，

∴∠QPC+∠PQC+∠PCQ=180°，

∴∠BAC=∠PQC+∠QPC．

【点睛】

本题考查平行线的判定与性质及角平分线的定义，两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；熟练掌握平行线的性质是解题关键．

2、（1）见解析；（2）15°或45°

【解析】

【分析】

（1）分当OC在外部时和当OC在内部时，两种情况，分别作图即可；

（2）根据（1）所求和角平分线，余角的定义求解即可．

【详解】

解：（1）如图所示，即为所求；

（2）当OC在外部时（如图1），

∵，与互余，

∴，

∴，

∴OP是的角平分线，

∴，

∴

当OC在内部时（如图2）

∵，与互余

∴，

∴

∴OP是的角平分线

∴

∴

综上：或45°．

【点睛】

本题主要考查了角平分线的定义，余角的定义，熟知角平分线和余角的定义是解题的关键．

3、（1），；（2）．

【解析】

【分析】

（1）根据互余的性质求出，根据角平分线的性质求出，结合图形计算即可；

（2）根据互余的性质用表示，根据角平分线的性质求出，结合图形列式计算即可．

【详解】

解：

（1）∵与互余，，

∴，

∵OE平分，

∴，

∴，

∴，；

（2）∵，且与互余，

∴，

∵OE平分，

∴，

∴，

解得：．

【点睛】

本题考查了余角及角平分线的性质，角的计算，理解两个性质并准确识图，理清图中各角度之间的关系是解题的关键．

4、（1）51°48′；（2）OG是∠EOB的平分线，理由见解析

【解析】

【分析】

（1）根据互为余角的意义和对顶角的性质，可得∠AOC＝∠BOD＝38°12′，进而求出∠BOG；

（2）求出∠EOG＝∠BOG即可．

【详解】

解：（1）∵OG⊥CD．

∴∠GOC＝∠GOD＝90°，

∵∠AOC＝∠BOD＝38°12′，

∴∠BOG＝90°﹣38°12′＝51°48′，

（2）OG是∠EOB的平分线，

理由：

∵OC是∠AOE的平分线，

∴∠AOC＝∠COE＝∠DOF＝∠BOD，

∵∠COE+∠EOG＝∠BOG+∠BOD＝90°，

∴∠EOG＝∠BOG，

即：OG平分∠BOE．

【点睛】

本题主要考查角平分线的定义及余角，熟练掌握角平分线的定义及余角是解题的关键．

5、（1）25°；（2）126°43ʹ；（3）15°36ʹ；（4）61°3ʹ．

【解析】

【分析】

（1）根据余角的性质，即可求解；

（2）根据补角的性质，即可求解；

（3）用 乘以∠AOB，即可求解；

（4）用3乘以∠AOB，即可求解．

【详解】

解：（1）∠AOB的余角的度数为

（2） ；  

（3） ；

（4）3∠AOB=3×20°21ʹ=60°63ʹ=61°3ʹ．

【点睛】

本题主要考查了余角和补角，角的倍分关系，熟练掌握余角和补角的性质，角的倍分关系是解题的关键．