高中数学优质课《函数的单调性》课件与教学设计3

这是一份高中数学优质课《函数的单调性》课件与教学设计3，文件包含《函数的单调性》教学课件ppt、《函数的单调性》教学设计doc、《函数的单调性》教学点评doc等3份课件配套教学资源，其中PPT共18页， 欢迎下载使用。

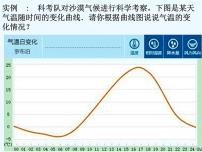
问题：从左至右，图象的变化趋势是什么？
f(x1)< f(x2)
问题：在区间D上的x1， x2，当x1< x2时，有f(x1)< f(x2)，一定能保证函数图象在区间D上是上升的吗？
如果函数 y =f(x)在区间D上是增函数或减函数，那么就说函数 y =f(x)在区间D上具有（严格的）单调性；
区间D就叫做函数y =f(x)的单调区间.
强调：多个单调增（减）区间用“，”“和”连接.
类型一：根据图象判断函数的单调性
类型二：利用定义证明函数的单调性
3. 增（减）函数概念的形成，经历了哪些过程？
1. 判定函数单调性的方法：
2.利用定义法证明函数单调性的步骤：
取值，作差变形，定号，下结论；
由图象直观感知 自然语言描述 数学符号语言描述
4.凭借直观的图象，我们能判断函数的单调性，为什 么还要用数学符号语言定义增（减）函数呢？
一、必做题：课本A组1，2；课时九；