数学6.3 平面向量基本定理及坐标表示示范课ppt课件

这是一份数学6.3 平面向量基本定理及坐标表示示范课ppt课件，共30页。PPT课件主要包含了平面向量基本定理，平面的基底有多少组，无数组，重要结论等内容，欢迎下载使用。
1.借助平面直角坐标系，掌握平面向量 的正交分解及坐标表示.
2.掌握两个向量加、减运算的坐标表示.
两个向量加、减运算的坐标表示
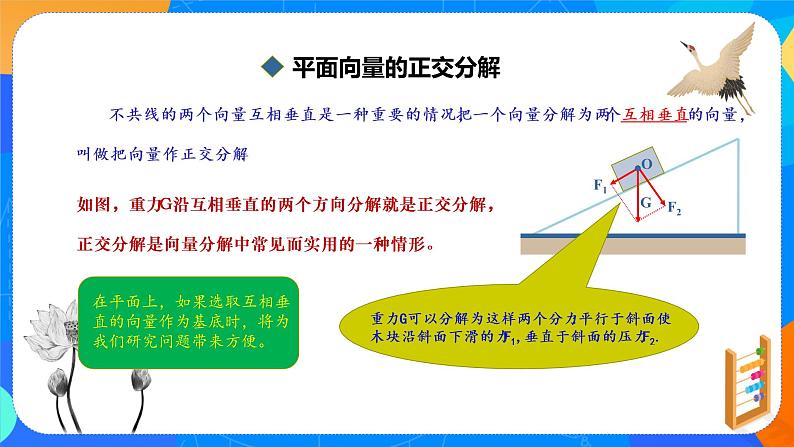
不共线的两个向量互相垂直是一种重要的情况，把一个向量分解为两个互相垂直的向量，叫做把向量作正交分解.
如图，重力G沿互相垂直的两个方向分解就是正交分解，正交分解是向量分解中常见而实用的一种情形。
在平面直角坐标系中,每个点都有一坐标与之对应，平面向量是否也有类似的表示呢?
向量的坐标与点的坐标关系
4.特殊向量的坐标：i＝ ，j＝ ，0＝————.
3.坐标表示：a＝ .
2.坐标：对于平面内的任意一个向量a，由平面向量基本定理可知，有且只有一 对实数x，y，使得a＝ ，则有序数对(x，y)叫做向量a的坐标.
1.基底：在平面直角坐标系中，设与x轴、y轴方向相同的两个________分别为i，j， 取{i，j}作为 .
注:对向量坐标表示的理解:
(1)任一平面向量都有唯一的坐标与之对应。
(3)相等的向量有相等的坐标.
(2)起点在坐标原点的向量的坐标为其终点的坐标。
结论：两个向量和（差）的坐标分别等于这两个向量相应坐标的和（差）.
结论：一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标。
结论2：相等的向量有相等的坐标.
结论1：起点在坐标原点的向量的坐标为其终点的坐标。
结论3：两个向量和（差）的坐标分别等于这两个向量相应坐标的和（差）.
结论4：一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标。
SI KAO BIAN XI PAN DUAN ZHENG WU
1.零向量的坐标是(0,0).(　　)2.两个向量的终点不同，则这两个向量的坐标一定不同.(　　)3.当向量的始点在坐标原点时，向量的坐标就是向量终点的坐标.(　　)4.向量可以平移，平移前后它的坐标发生变化.(　　)
例6 如图所示，已知平行四边形ABCD的三个顶点A、B、C的坐标分别为A(－2,1)， B(－1,3)，C(3,4)，求点D的坐标。
解一 如图所示，设顶点D的坐标为D(x,y)，
所以顶点D的坐标为D(2,2).
解二 如图所示，由向量加法的平行四边形法则可知：
1.已知向量a＝(1,2)，b＝(3,1)，则b－a等于（ ） A.(－2,1) B.(2，－1) C.(2,0) D.(4,3)
解 由题意得b－a＝(3,1)－(1,2)＝(2，－1).
故点C的坐标为(0,4).
KE TANG XIAO JIE
1.知识点： (1)平面向量的正交分解及坐标表示.
2.方法归纳：数形结合.
(2)平面向量加、减运算的坐标表示.
课本P30 练习 1,2,3