初中数学北京课改版七年级下册第五章 二元一次方程组综合与测试练习题

这是一份初中数学北京课改版七年级下册第五章 二元一次方程组综合与测试练习题，共19页。试卷主要包含了设m为整数，若方程组的解x，二元一次方程组的解是等内容，欢迎下载使用。
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、若是方程组的解，则的值为（ ）
A．16B．-1C．-16D．1
2、如图，用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形，则每个小长方形的周长是（ ）
A．60厘米B．80厘米C．100厘米D．120厘米
3、用加减法解方程组由②-①消去未知数，所得到的一元一次方程是（ ）
A．B．C．D．
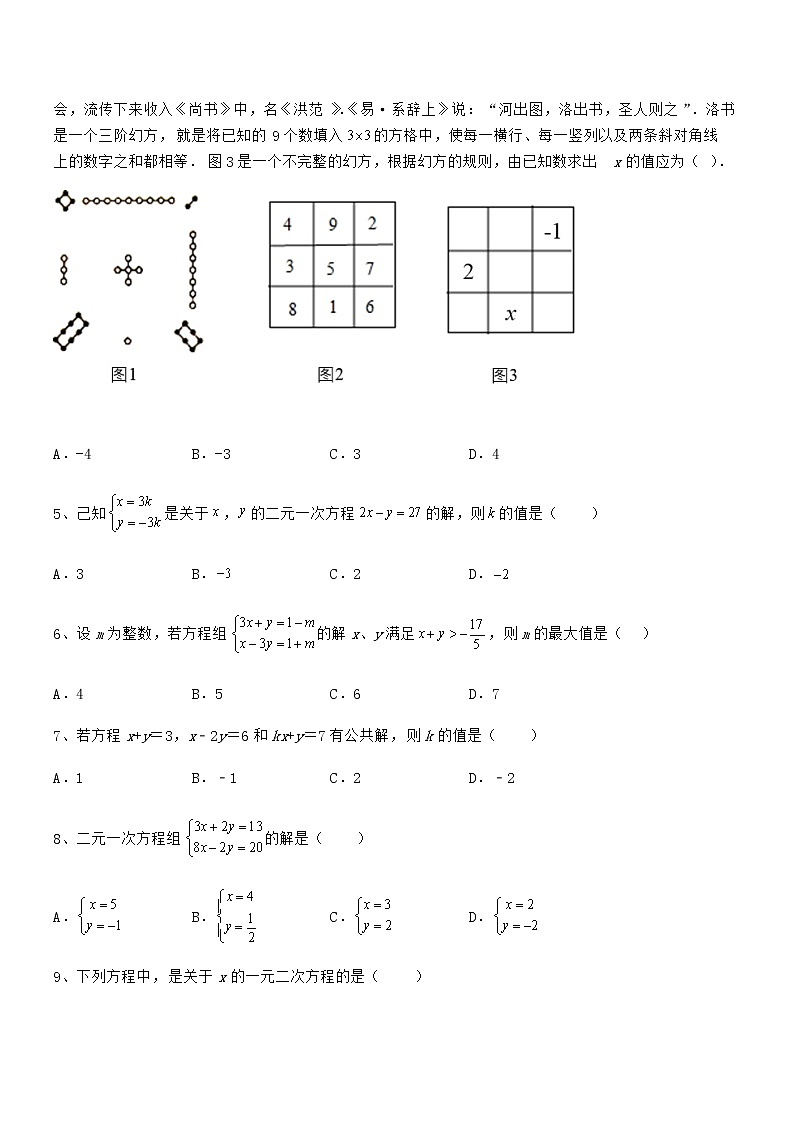
4、图1是我国古代传说中的洛书，图2是洛书的数字表示．相传，大禹时，洛阳西洛宁县洛河中浮出神龟，背驮“洛书”，献给大禹．大禹依此治水成功，遂划天下为九州．又依此定九章大法，治理社会，流传下来收入《尚书》中，名《洪范》．《易·系辞上》说：“河出图，洛出书，圣人则之”．洛书是一个三阶幻方，就是将已知的9个数填入的方格中，使每一横行、每一竖列以及两条斜对角线上的数字之和都相等．图3是一个不完整的幻方，根据幻方的规则，由已知数求出 x的值应为（ ）．
A．-4B．-3C．3D．4
5、己知是关于，的二元一次方程的解，则的值是（ ）
A．3B．C．2D．
6、设m为整数，若方程组的解x、y满足，则m的最大值是（ ）
A．4B．5C．6D．7
7、若方程x+y＝3，x﹣2y＝6和kx+y＝7有公共解，则k的值是（ ）
A．1B．﹣1C．2D．﹣2
8、二元一次方程组的解是（ ）
A．B．C．D．
9、下列方程中，是关于x的一元二次方程的是（ ）
A．x（x－2）＝0B．x2－1－y＝0C．x2＋1＝x2－2xD．ax2＋c＝0
10、《九章算术》是我国古代一部著名的算书，它的出现标志着中国古代数学形成了完整的体系，其中卷八方程[七]中记载：“今有牛五，羊二，直金十两；牛二、羊五，直金八两，问牛、羊直金几何？”译文：“假设有5头牛，2只羊共值金10两；2头牛，5只羊共值金8两，问每头牛、每只羊各值金多少两？”设每头牛值金x两，每只羊值金y两，那么下面列出的方程组中正确的是（ ）
A．B．C．D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、已知方程组的解是，则的值为________．
2、若与可以合并成一项，则m+n的值_____．
3、一元二次方程x﹣3y＝8写成用含y的代数式表示x的形式为______．
4、小明从邮局买了面值0.5元和0.8元的邮票共9枚，花了6.3元，小明买了两种邮票各多少枚？若设买了面值0.5元的邮票x枚，0.8元的邮票y枚，则根据题意可列出方程组为__________．
5、若x，y满足方程组，则化数式的值为 _____．
三、解答题（5小题，每小题10分，共计50分）
1、解方程组
（1） （2）
2、解方程组：
（1） （2）
3、疫情期间，某物业公司欲购进A、B两种型号的防护服，若购入A种防护服30套，B种防护服50套，需6600元，若购入A种防护服40套，B种防护服10套，需3700元．
（1）求购进A、B两种防护服的单价分别是多少元？
（2）若该公司准备用不多于12300元的金额购进这两种防护服共150套，求A种防护服至少要购进多少套？
4、列二元一次方程组解应用题：某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱，矿泉水的成本价和销售价如表所示：
（1）该大型超市购进A、B品牌矿泉水各多少箱？
（2）全部销售完600箱矿泉水，该超市共获得多少利润？
5、解下列方程组：
（1）；
（2）．
---------参考答案-----------
一、单选题
1、C
【分析】
把x与y的值代入方程组，求出a+b与a-b的值，代入原式计算即可求出值．
【详解】
解：把代入方程组得，
两式相加得；
两式相差得：，
∴，
故选C．
【点睛】
本题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
2、D
【分析】
设小长方形的长为x，小长方形的宽为y，根据题意列出二元一次方程组求解即可；
【详解】
设小长方形的长为x，小长方形的宽为y，
根据题意可得：，
解得：，
∴每个小长方形的周长是；
故选D．
【点睛】
本题主要考查了二元一次方程组的应用，准确计算是解题的关键．
3、A
【分析】
观察两方程发现y的系数相等，故将两方程相减消去y即可得到关于x的一元一次方程．
【详解】
解：解方程组，由②-①消去未知数y，所得到的一元一次方程是2x=9，
故选：A．
【点睛】
本题考查了解二元一次方程组，利用了消元的思想，消元的方法有：加减消元法与代入消元法．
4、A
【分析】
如图所示，其中a、b、c、d表示此方格中表示的数，则可得由此即可得到④，⑤，然后把④⑤代入③中即可求解．
【详解】
解：如图所示，其中a、b、c、d表示此方格中表示的数，
由题意得：，
由①得④，
由②得⑤，
把④和⑤代入③中得，
∴，
故选A．
【点睛】
本题主要考查了解方程组，解题得关键在于能够利用整体代入的思想进行求解．
5、A
【分析】
将代入关于x，y的二元一次方程2x-y=27得到关于k的方程，解这个方程即可得到k的值．
【详解】
解：将代入关于x，y的二元一次方程2x-y=27得：
2×3k-（-3k）=27．
∴k=3．
故选：A．
【点睛】
本题主要考查了二元一次方程的解和解一元一次方程，将方程的解代入原方程是解题的关键．
6、B
【分析】
先把m当做常数，解一元二次方程，然后根据得到关于m的不等式，由此求解即可
【详解】
解：
把①×3得：③，
用③+①得：，解得，
把代入①得，解得，
∵，
∴，即，
解得，
∵m为整数，
∴m的最大值为5，
故选B．
【点睛】
本题主要考查了解二元一次方程组和解一元一次不等式和求不等式的整数解，解题的关键在于能够熟练掌握解二元一次方程组的方法．
7、C
【分析】
先求出的解，然后代入kx+y＝7求解即可．
【详解】
解：联立，
②-①，得
-3y=3，
∴y=-1，
把y=-1代入①，得
x-1=3
∴x=4，
∴，
代入kx+y＝7得：4k﹣1＝7，
∴k＝2，
故选：C．
【点睛】
本题考查了解二元一次方程组，解二元一次方程组的基本思路是消元，二元方程转化为一元方程是解题的关键．
8、C
【分析】
根据加减消元法，由①+②得出11x＝33，求出x，再把x＝3代入①求出y即可．
【详解】
解：，
由①+②，得11x＝33，
解得：x＝3，
把x＝3代入①，得9+2y＝13，
解得：y＝2，
所以方程组的解是，
故选：C．
【点睛】
本题考查了解二元一次方程组，解题的关键是掌握加减消元法解方程组．
9、A
【分析】
根据一元二次方程的定义，对选项逐个判断即可，一元二次方程是指化简后，只含有一个未知数并且未知数的次数为2的整式方程．
【详解】
解：A、含有一个未知数，且未知数次数为2，为一元二次方程，符合题意；
B、含有两个未知数，不是一元二次方程，不符合题意；
C、，含有一个未知数，不是一元二次方程，不符合题意；
D、当时，不是一元二次方程，不符合题意；
故选：A
【点睛】
此题考查了一元二次方程的定义，解题的关键是理解一元二次方程的概念．
10、A
【分析】
根据题意可直接进行求解．
【详解】
解：设每头牛值金x两，每只羊值金y两，由题意得：；
故选A．
【点睛】
本题主要考查二元一次方程组的应用，熟练掌握二元一次方程的应用是解题的关键．
二、填空题
1、
【解析】
【分析】
将代入方程组，得到关于的方程组，然后求解即可．
【详解】
解：将代入方程组，得
①②，得，解得
将代入得，，解得
∴
故答案为：
【点睛】
此题考查了二元一次方程租的求解以及二元一次方程组的解，解题的关键是掌握二元一次方程组的求解方法．
2、2
【解析】
【分析】
先根据同类项的定义（如果两个单项式，它们所含字母相同，并且相同字母的指数也分别相同，那么这两个单项式是同类项）可得一个关于二元一次方程组，解方程组求出的值，再代入计算即可得．
【详解】
解：由题意得：与是同类项，
则，
解得，
所以，
故答案为：2．
【点睛】
本题考查了同类项、二元一次方程组的应用，熟记同类项的定义是解题关键．
3、3y+8##8+3y
【解析】
【分析】
移项，利用等式的性质变形即可．
【详解】
解: x﹣3y＝8
x=3y+8
故答案为:3y+8
【点睛】
本题属于二元一次方程变形的问题，依据等式的性质变形即可．本题比较简单．
4、
【解析】
【分析】
由题意可得等量关系①0.5元的邮票枚数+面值0.8元的邮票枚数=9枚；②0.5元的邮票价格+面值0.8元的邮票总价格=6.3元，由等量关系列出方程组即可．
【详解】
解：设买了面值0.5元的邮票x枚，0.8元的邮票y枚，由题意得
，
故答案为：．
【点睛】
此题主要考查了由实际问题抽象出二元一次方程组，关键是找到题目中的等量关系，列出方程组．
5、0
【解析】
【分析】
二元一次方程组两式相加得x+y=2，两式相减得x-y=4，将结果代入=0．
【详解】
∵
令有
∴
令有
∴
将，代入得
．
故答案为：0．
【点睛】
本题考查了已知式子的值解代数式值和解二元一次方程组，通过加减消元法化简二元一次方程组，得出所求代数式中含有的部分，再代入计算即可．
三、解答题
1、（1）；（2）．
【分析】
（1）利用代入消元法解方程组即可得；
（2）利用加减消元法解方程组即可得．
【详解】
解：（1），
将①代入②得：，
解得，
将代入①得：，即，
则方程组的解为；
（2），
由①②得：，
解得，
将代入①得：，
解得，
则方程组的解为．
【点睛】
本题考查了解二元一次方程组，熟练掌握消元法是解题关键．
2、（1）；（2）．
【分析】
（1）应用加减消元法，求出方程组的解即可；
（2）先把方程组化简，再应用加减消元法，求出方程组的解即可．
【详解】
解：（1），
①×2得，6x+2y=30③，
②+③得，11x=44，
解得x=4，
把x=4代入①得，y=3，
所以方程组的解是；
（2），
整理得，
①×2得，4x+6y=20③，
③-②得，5y=15，
解得y=3，
把y=3代入①得，x=，
所以方程组的解是．
【点睛】
本题考查了二元一次方程组的解，熟练掌握加减消元法和代入消元法解二元一次方程组是解题的关键．
3、（1）购进A、B两种防护服的单价分别是70元、90元；（2）A种防护服至少要购进60套
【分析】
（1）根据题意可以列出相应的二元一次方程组，然后求解即可；
（2）根据题意可以列出相应的不等式，然后求解即可．
【详解】
解：（1）设购进A、B两种防护服的单价分别是a元、b元，
由题意可得： ，
解得：，
答：购进A、B两种防护服的单价分别是70元、90元；
（2）设购进A种防护服x套，则购进B种防护服（150﹣x）套，
由题意可得70x+90（150﹣x）≤12300，
即：
解得：x≥60，
答：A种防护服至少要购进60套．
【点睛】
本题考查二元一次方程组的实际应用，以及一元一次不等式的应用，能够列出相关的方程组或不等关系是解题的重点．
4、（1）A品牌矿泉水400箱，B品牌矿泉水200箱；（2）7800元
【分析】
（1）设该大型超市购进A品牌矿泉水x箱，B品牌矿泉水y箱，根据该超市购进A、B两种品牌的矿泉水共600箱且共花费15000元，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）利用总利润＝每箱的销售利润×销售数量（购进数量），即可求出结论．
【详解】
解：（1）设该大型超市购进A品牌矿泉水x箱，B品牌矿泉水y箱，
依题意得：，
解得：．
答：该大型超市购进A品牌矿泉水400箱，B品牌矿泉水200箱．
（2）（元）．
答：全部销售完600箱矿泉水，该超市共获得7800元利润．
【点睛】
本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．
5、（1） ；（2）
【分析】
利用加减消元法，即可求解．
【详解】
解：（1）
由①×3-②，得： ，
解得： ，
把代入①，得： ，
解得： ，
所以方程组的解为 ；
（2），
由①×2-②×3，得： ，
解得： ，
把代入②，得： ，
解得： ，
所以方程组的解为 ．
【点睛】
本题主要考查了解二元一次方程组，熟练掌握二元一次方程组的解法——代入消元法和加减消元法是解题的关键．
类别/单价
成本价（元/箱）
销售价（元/箱）
A品牌
20
32
B品牌
35
50