高中数学苏教版 (2019)选择性必修第二册6.1空间向量及其运算优秀课件ppt

这是一份高中数学苏教版 (2019)选择性必修第二册6.1空间向量及其运算优秀课件ppt，共60页。PPT课件主要包含了学习目标，随堂演练，课时对点练，共面向量，共面向量定理，内容索引，同一平面，解析如图所示，x＋y＋z＝1，课堂小结等内容，欢迎下载使用。
1.了解共面向量的概念.2.理解空间共面向量定理，会证明直线与平面平行.3.理解空间向量共面的充要条件，会证明空间四点共面.
在平面向量中，向量b与向量a(a≠0)共线的充要条件是存在实数λ，使得b＝λa.那么，空间任意一个向量p与两个不共线的向量a，b共面时，它们之间存在什么样的关系呢？
三、空间四点共面的条件
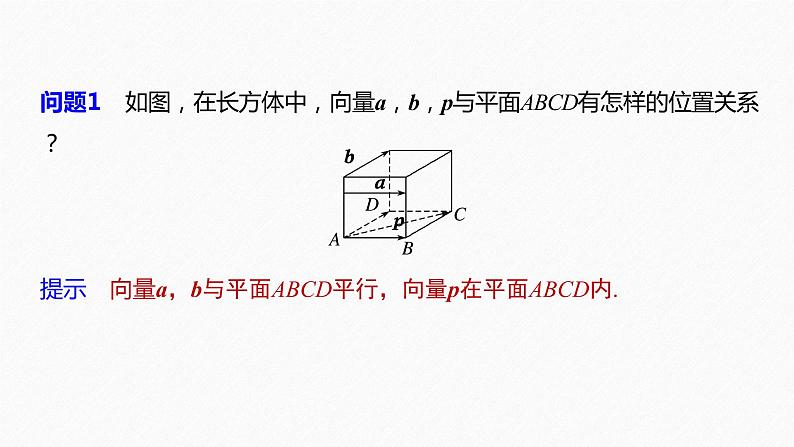
问题1　如图，在长方体中，向量a，b，p与平面ABCD有怎样的位置关系？
提示　向量a，b与平面ABCD平行，向量p在平面ABCD内.
能平移到 内的向量叫作共面向量.注意点：(1)共面向量不仅包括在同一个平面内的向量，还包括平行于同一平面的向量.(2)空间任意两个向量是共面的，但空间任意三个向量就不一定共面了.
A.有相同起点的向量 B.等长向量C.共面向量 D.不共面向量
三个向量的模不一定相等，故B错误；
反思感悟　若a，b不共线且同在平面α内，则p与a，b共面的意义是p在α内或p∥α.
跟踪训练1　(多选)下列说法错误的是A.空间的任意三个向量都不共面B.空间的任意两个向量都共面C.三个向量共面，即它们所在的直线共面D.若三向量两两共面，则这三个向量一定也共面
如果两个向量a，b不共线，那么向量p与向量a，b共面的充要条件是存在有序实数组(x，y)，使得p＝xa＋yb，即向量p可以由两个不共线的向量a，b线性表示.注意点：(1)a，b不共线.(2)也可说成向量p由不共线的向量a，b线性表示.
(2)如图，在底面为正三角形的斜棱柱ABC－A1B1C1中，D为AC的中点.求证：AB1∥平面C1BD.
又由于AB1不在平面C1BD内，所以AB1∥平面C1BD.
反思感悟　如果两个向量a，b不共线，则向量p与向量a，b共面的充要条件是存在有序实数组(x，y)，使p＝xa＋yb.在判断空间的三个向量共面时，注意“两个向量a，b不共线”的要求.
求证：MN∥平面ABB1A1.
＝(1－k)a＋kb，
＝(1－k)a－kc，
∵MN不在平面ABB1A1内，∴MN∥平面ABB1A1.
提示　x＋y＋z＝1.证明如下：(1)充分性
∴点P与A，B，C共面.(2)必要性∵点P在平面ABC内，且点A，B，C不共线，
且点O在平面ABC外，
∴x＝1－m－n，y＝m，z＝n，∴x＋y＋z＝1.
若空间任意无三点共线的四点，对于空间任一点O，存在实数x，y，z使得 ，且x，y，z满足 ，则A，B，C，D四点共面.
例3　(1)(多选)对空间任一点O和不共线的三点A，B，C，能得到P，A，B，C四点共面的是
由共面的充要条件知P，A，B，C四点共面，故C选项正确；
(2)在长方体ABCD－A1B1C1D1中，点M为DD1的中点，点N在AC上，且AN∶NC＝2∶1，求证：A1，B，N，M四点共面.
又∵三向量有相同的起点A1，∴A1，B，N，M四点共面.
反思感悟　解决向量共面的策略
(2)证明三个向量共面(或四点共面)，需利用共面向量定理，证明过程中要灵活进行向量的分解与合成，将其中一个向量用另外两个不共线的向量来表示.
跟踪训练3　已知E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，求证：(1)E，F，G，H四点共面.
证明　如图，连接EG，BG.
(2)BD∥平面EFGH.
所以EH∥BD.又EH⊂平面EFGH，BD⊄平面EFGH，所以BD∥平面EFGH.
1.知识清单：(1)共面向量定理的概念及应用.(2)空间中应用共面向量定理判断共面问题.2.方法归纳：类比法.
1.对于空间的任意三个向量a，b,2a－b，它们一定是A.共面向量 B.共线向量C.不共面向量 D.既不共线也不共面的向量
解析　由向量共面定理可知，三个向量a，b,2a－b为共面向量.
解析　A选项中，3－1－1＝1，四点共面，
且M，A，B，C四点共面，
1.已知i与j不共线，则存在两个非零常数m，n，使k＝mi＋nj是i，j，k共面的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件
解析　若i与j不共线，且存在两个非零常数m，n，使k＝mi＋nj，则由共面向量定理，知i，j，k共面.若i与j不共线，且k与i，j共面，则存在唯一的一对实数(m，n)，使k＝mi＋nj，但m，n不一定为非零常数，故选A.
2.已知两非零向量e1，e2，且e1与e2不共线，设a＝λe1＋μe2(λ，μ∈R，且λ，μ≠0)，则下列结论正确的是A.a∥e1B.a∥e2C.a与e1，e2共面D.以上三种情况均有可能
解析　假设a与e1共线，则a＝ke1，所以a＝λe1＋μe2可变为(k－λ)e1＝μe2，所以e1与e2共线，这与e1与e2不共线相矛盾，故假设不成立，则A不正确，同理B不正确，则D也错误.
A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分又不必要条件
解析　空间任意一点O和不共线的三点A，B，C，
则P，A，B，C四点共面等价于x＋y＋z＝1；若x＝2，y＝－3，z＝2，则x＋y＋z＝1，所以P，A，B，C四点共面；若P，A，B，C四点共面，则x＋y＋z＝1，但不能得到x＝2，y＝－3，z＝2，所以x＝2，y＝－3，z＝2是P，A，B，C四点共面的充分不必要条件.
C.A，B，C，D四点不共面D.A，B，C，D四点共面
故A，B，C，D四点共面，故C错误，D正确.
6.(多选)下列命题中是真命题的为A.若向量p＝xa＋yb，则p与a，b共面B.若p与a，b共面，则p＝xa＋ybC.若＝x＋y，则P，M，A，B四点共面
解析　对于选项A，由共面向量定理得p与a，b共面，A是真命题；对于选项B，若a，b共线，p不一定能用a，b表示出来，B是假命题；
7.下列命题中为真命题的是_____.
解析　在空间四边形A1A2A3A4中，
但四点不一定共面，故②③都错误.
又∵P是空间任意一点，A，B，C，D四点满足任意三点均不共线，但四点共面，
(2)判断M是否在平面ABC内.
10.如图，直三棱柱ABC－A′B′C′，点M，N分别为A′B和B′C′的中点，证明：MN∥平面A′ACC′.
且点M，N分别为A′B和B′C′的中点，
因为MN⊄平面A′ACC′，所以MN∥平面A′ACC′.
11.下面关于空间向量的说法正确的是A.若向量a，b平行，则a，b所在直线平行B.若向量a，b所在直线是异面直线，则a，b不共面
解析　我们可以通过平移将空间中任意两个向量平移到一个平面内，因此空间任意两个向量都是共面的，故B，C错误；由向量平行与直线平行的区别，可知A错误；
A.在平面BAD1内 B.在平面BA1D内C.在平面BA1D1内 D.在平面AB1C1内
于是M，B，A1，D1四点共面.
∴点P与点A，B，C共面.
解析　连结BD，BG(图略).
且G，B，P，D四点共面，
求证：(1)A，B，C，D四点共面，E，F，G，H四点共面；