
2021学年第十七章 方差与频数分布综合与测试同步练习题
展开京改版八年级数学下册第十七章方差与频数分布综合练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
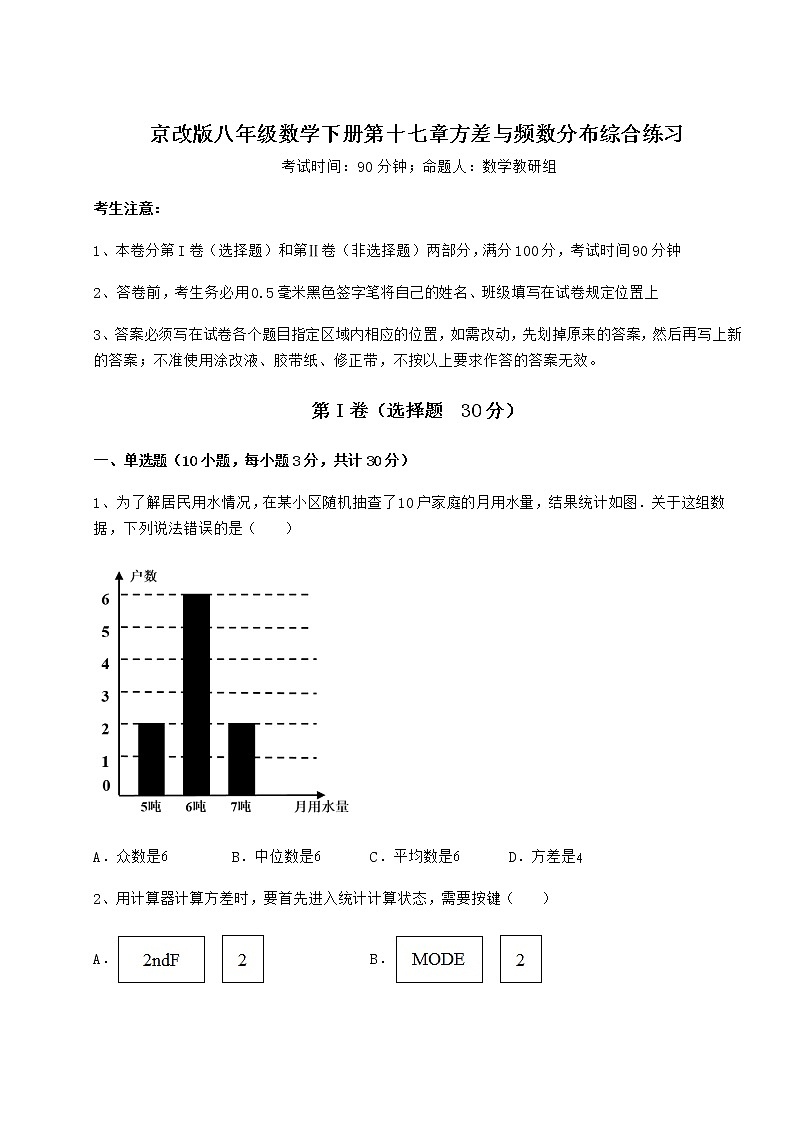
1、为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图.关于这组数据,下列说法错误的是( )
A.众数是 B.中位数是 C.平均数是 D.方差是
2、用计算器计算方差时,要首先进入统计计算状态,需要按键( )
A. B.
C. D.
3、已知数据1,2,3,3,4,5,则下列关于这组数据的说法错误的是( )
A.平均数、中位数和众数都是3
B.极差为4
C.方差是
D.标准差是
4、某手机公司新推出了四款新型手机,公司为了了解各款手机的性能,随机抽取了每款手机各50台进行测试,以下是四款手机的性能得分(满分100分,分数越高,性能越好)的平均分和方差,则这四款新型手机中性能好且稳定的是( )
| ||||
平均成绩(分) | 95 | 98 | 96 | 98 |
方差 | 3 | 3 | 2 | 2 |
A. B. C. D.
5、已知一组数据8,6,10,10,13,11,8,10,12,12,9,8,7,12,9,11,9,10,11,10.那么频率是0.2的一组数据的范围是( )
A. B. C. D.
6、某班在体育活动中,测试了十位学生的“一分钟跳绳”成绩,得到十个各不相同的数据.在统计时,出现了一处错误:将最高成绩写得更高了,则计算结果不受影响的是( )
A.平均数 B.中位数 C.方差 D.众数
7、已知一组数据有80个,其中最大值为140,最小值为40,取组距为10,则可分成( ).
A.11组 B.9组 C.8组 D.10组
8、甲、乙、丙、丁四名跳高运动员最近10次训练成绩的平均数与方差如表所示.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择的是( )
| 甲 | 乙 | 丙 | 丁 |
平均数/m | 180 | 180 | 185 | 185 |
方差 | 8.2 | 3.9 | 75 | 3.9 |
A.甲 B.乙 C.丙 D.丁
9、甲、乙两人各射击5次,成绩如表.根据数据分析,在两人的这5次成绩中( )
| 成绩(单位:环) | ||||
甲 | 3 | 7 | 8 | 8 | 10 |
乙 | 7 | 7 | 8 | 9 | 10 |
A.甲的平均数大于乙的平均数
B.甲的中位数小于乙的中位数
C.甲的众数大于乙的众数
D.甲的方差小于乙的方差
10、2022年冬季奥运会将在北京张家口举行,如表记录了四名短道速滑选手几次选拔赛成绩的平均数和方差s2.
| 甲 | 乙 | 丙 | 丁 |
平均数(单位:秒) | 52 | m | 52 | 50 |
方差s2(单位:秒2) | 4.5 | n | 12.5 | 17.5 |
根据表中数据,可以判断乙选手是这四名选手中成绩最好且发挥最稳定的运动员,则m、n的值可以是( )
A.m=50,n=4 B.m=50,n=18 C.m=54,n=4 D.m=54,n=18
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、南京2021年11月1号的最高气温为22℃,最低气温为12℃,该日的气温极差为 __.
2、小宇调查了初一年级三个班学生的身高,并进行了统计,列出如下频数分布表:
身高/厘米 频数 班级 | 150≤x<155 | 155≤x<160 | 160≤x<165 | 165≤x<170 | 170≤x<175 | 合计 |
1班 | 1 | 8 | 12 | 14 | 5 | 40 |
2班 | 10 | 15 | 10 | 3 | 2 | 40 |
3班 | 5 | 10 | 10 | 8 | 7 | 40 |
若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示,不考虑其他因素的影响,则 _____(填“1班”,“2班”或“3班”)的可供挑选的空间最大.
3、某果农随机从甲、乙、丙三个品种的批把树中各选5棵,每棵产量的平均数(单位:千克)及方差(单位:千克2)如表所示,他准备从这三个品种中选出一种产量既高又稳定的批把树进行种植,则应选的品种是 __.
| 甲 | 乙 | 丙 |
45 | 45 | 42 | |
S2 | 1.8 | 2.3 | 1.8 |
4、一组数据5, 4, 2, 4, 5的方差是________.
5、某校九年级进行了3次体育中考项目﹣﹣1000米跑的模拟测试,甲、乙、丙三位同学3次模拟测试的平均成绩都是3分55秒,三位同学成绩的方差分别是s甲2=0.01,s乙2=0.009,s丙2=0.0093.则甲、乙、丙三位同学中成绩最稳定的是 ___.
三、解答题(5小题,每小题10分,共计50分)
1、 “中国梦”是中华民族每一个人的梦,各中小学开展经典诵读活动,是“中国梦”教育这一宏大乐章里的响亮音符某学校在经典诵读活动中,对全校学生用A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行评价,现从中抽取若干名学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少名学生进行调查;
(2)将图甲中的条形统计图补充完整;
(3)求出图乙中D等级所对应的扇形圆心角的度数;
(4)根据抽样调查的结果,请你估计该校2000名学生中有多少名学生获得B等级的评价.
2、重庆北关中学有甲,乙两个学生食堂,为了了解哪个食堂更受学生欢迎,学校开展了为期20天的的数据收集工作,统计初三年级每天中午分别到甲,乙食堂就餐的人数,现对收集到的数据进行整理、描述和分析(人数用x(人)表示,共分成四个等级,A:250<x≤300;B:200<x≤250;C:150<x≤200;D:100<x≤150),下面给出了部分信息:
甲、乙食堂的人数统计表:
食堂 | 甲 | 乙 |
平均数 | 211 | 196 |
中位数 | a | 215 |
众数 | b | 230 |
极差 | 188 | c |
甲食堂20天的所有人数数据为:112,125,138,146,168,177,177,177,185,218,230,234,241,246,249,260,260,279,298,300
乙食堂20天的人数数据中最少人数为120人,A等级的数据为278,290,260
请根据相关信息,回答以下问题:
(1)填空:a= ,b= ,c= ,并补全乙食堂的人数数据条形统计图:
(2)根据以上数据,请判断哪个食堂的更受同学们欢迎,并说明理由(一条即可);
(3)已知该校初三年级共有学生400人,全校共有学生1600人,请估算北关中学甲食堂每天中午大约准备多少名同学的午餐?
3、为弘扬中华传统文化,某校开展“戏剧进课堂”活动.该校随机抽取部分学生,四个类别:表示“很喜欢”,表示“喜欢”,表示“一般”,表示“不喜欢”,调查他们对戏剧的喜爱情况,将结果绘制成如图两幅不完整的统计图
根据图中提供的信息,解决下列问题:
(1)此次共调查了 名学生;
(2)请补全类条形统计图;
(3)扇形统计图中.类所对应的扇形圆心角的大小为 度;
(4)该校共有1560名学生,估计该校表示“很喜欢”的类的学生有多少人?
4、在精准扶贫的政策下,某贫困户在当地政府的支持和帮助下办起了养殖业,经过一段时间的精心饲养,总量为6000只的一批兔子达到了出售标准,现从这批兔中随机选择部分进行称重,将得到的数据用下列统计图表示(频数分布直方图每组含前一个边界值,不含后一个边界值).根据以上信息,解答下列问题:
(1)补全图中的频数分布直方图;
(2)估计这批兔子中质量不小于1.7kg的有多少只.
5、为落实“每天锻炼一小时,快乐学习一整天”的要求,某校举行校园阳光大课间活动,为了解七年级学生每周在校体育锻炼时间,随机抽取了部分学生进行调查,并绘制了以下不完整的频数分布表和频数分布直方图.
时间/小时 | 频数 | 百分比 |
4 | b | |
10 | 25% | |
a | 15% | |
8 | 20% | |
12 | 30% |
(1)本次调查的学生总人数为______;
(2)求a、b的值,并补全频数分布直方图;
(3)若将调查结果绘制成扇形统计图,求锻炼时间在“”所对应的扇形圆心角的度数.
-参考答案-
一、单选题
1、D
【分析】
根据统计图得出10户家庭的用水量数据,求得众数,中位数,平均数,方差,进而逐项判断即可
【详解】
根据统计图可得这10户家庭的用水量分别为:5,5,6,6,6,6,6,6,7,7
其中6出现了6次,次数最多,故众数是6,故A选项正确,不符合题意;
这组数据的中位数为:6,故B选项正确,不符合题意;
这组数据的平均数为,故C选项正确,不符合题意;
这组数据的方差为:,故D选项不正确,符合题意.
故选D.
【点睛】
本题考查了求众数,中位数,平均数,方差,掌握方差的计算公式是解题的关键.方差的计算公式:.
2、B
【分析】
由于不同的计算器,其操作不完全相同,可以根据计算器的说明书进行操作.
【详解】
解:用计算器求方差的一般步骤是:
①使计算器进入MODE 2状态;
②依次输入各数据;
③按求的功能键,即可得出结果.
故选:B.
【点睛】
本题主要考查了计算器求方差,正确掌握计算器的基本使用方法是解题关键.
3、D
【分析】
分别求出这组数据的平均数、众数、中位数、极差、方差、标准差,再进行判断.
【详解】
解:这组数据的平均数为:(1+2+3+3+4+5)÷6=3,出现次数最多的是3,排序后处在第3、4位的数都是3,因此众数和中位数都是3,因此选项A不符合题意;
极差为5﹣1=4,B选项不符合题意;
S2=×[(1﹣3)2+(2﹣3)2+(3﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=,C选项不符合题意;
S=,因此D选项符合题意,
故选:D.
【点睛】
考查平均数、中位数、众数、方差、标准差的计算方法,正确的计算是解答的前提.
4、D
【分析】
先根据平均成绩选出,然后根据方差的意义求出
【详解】
解:根据平均数高,平均成绩好得出的性能好,
根据方差越小,数据波动越小可得出的性能好,
故选:D
【点睛】
本题主要考查了平均数和方差,熟练掌握平均数和方差的意义是解答本题的关键
5、D
【分析】
首先知共有20个数据,根据公式:频数=频率×总数,知要使其频率为0.2,其频数应为4,然后观察选项中哪组数据包含样本中的数据有4个即可求解.
【详解】
解:这组数据共20个,要使其频率为0.2,则频数为:20×0.2=4个,
选项A中包含的数据有:6和7,其频数为2;
选项B中包含的数据有:8,8,8,9,9,9,其频数为6;
选项C中包含的数据有:10,10,10,10,10,11,11,11,其频数为8;
选项D中包含的数据有:12,12,12,13,其频数为4,
故选:D.
【点睛】
本题考查了频数与频率的概率,掌握公式“频数=频率×总数”是解决本题的关键.
6、B
【分析】
根据中位数的特点,与最高成绩无关,则计算结果不受影响,据此即可求得答案
【详解】
根据题意以及中位数的特点,因为中位数是通过排序得到的,所以它不受最大、最小两个极端数值的影响,
故选B
【点睛】
本题考查了中位数,平均数,方差,众数,理解中位数的意义是解题的关键,中位数是另外一种反映数据的中心位置的指标,其确定方法是将所有数据以由小到大的顺序排列,位于中央的数据值就是中位数, 因为中位数是通过排序得到的,所以它不受最大、最小两个极端数值的影响,而且部分数据的变动对中位数也没有影响.
7、A
【分析】
据组数=(最大值-最小值)÷组距计算即可得解,注意小数部分要进位.
【详解】
解:由组数=(最大值-最小值)÷组距可得:
组数=(140-40)÷10+1=11,
故选择:A
【点睛】
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
8、D
【分析】
首先比较平均数,平均数相同时选择方差较小的运动员参加.
【详解】
解:∵,
∴从丙和丁中选择一人参加比赛,
∵S丙2>S丁2,
∴选择丁参赛,
故选:D.
【点睛】
此题考查了平均数和方差,正确理解方差与平均数的意义是解题关键.
9、C
【分析】
根据题意求出众数,中位数,平均数和方差,然后进行判断即可.
【详解】
解:A、甲的成绩的平均数=(3+7+8+8+10)=7.2(环),乙的成绩的平均数=(7+7+8+9+10)=8.2(环),所以A选项说法错误,不符合题意;
B、甲的成绩的中位数为8环.乙的成绩的中位数为8环,所以B选项说法错误,不符合题意;
C、甲的成绩的众数为8环,乙的成绩的众数为7环;所以C选项说法正确,符合题意;
D、,,所以D选项说法错误,不符合题意.
故选C.
【点睛】
本题主要考查了平均数,众数,中位数和方差,解题的关键在于能够熟练掌握相关知识进行求解.
10、A
【分析】
根据乙选手是这四名选手中成绩最好且发挥最稳定的运动员,可得到乙选手的成绩的平均数最大,方差最小,即可求解.
【详解】
解:因为乙选手是这四名选手中成绩最好的,
所以乙选手的成绩的平均数最小,
又因为乙选手发挥最稳定,
所以乙选手成绩的方差最小.
故选:A.
【点睛】
本题主要考查了平均数和方差的意义,理解方差是反映一组数据的波动大小的一个量:方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.
二、填空题
1、10℃
【分析】
用最高温度减去最低温度即可.
【详解】
解:该日的气温极差为22﹣12=10(℃).
故答案为:10℃.
【点睛】
本题考查了有理数减法,解题的关键是了解有理数减法法则在生活中运用方法,难度不大.
2、1班
【分析】
根据各个班身高在160cm和170cm之间同学的人数,进行判断即可.
【详解】
解:身高在160cm和170cm之间同学人数:1班26人,2班13人,3班18人,因此可挑选空间最大的是1班,
故答案为:1班.
【点睛】
此题考查频数分布表的表示方法,从表格中获取数据和数据之间的关系是正确判断的前提.
3、甲
【分析】
先比较平均数得到甲和乙产量较高,然后比较方差得到甲比较稳定.
【详解】
解:因为甲、乙的平均数比丙大,所以甲、乙的产量较高,
又甲的方差比乙小,所以甲的产量比较稳定,
即从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是甲;
故答案为:甲.
【点睛】
本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则与平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数.
4、1.2
【分析】
首先求出平均数,然后根据方差的计算法则求出方差.
【详解】
解:平均数,
数据的方差 ,
故答案为 :1.2.
【点睛】
本题主要考查了求方差,解题的关键在于能够熟练掌握求方差的方法.
5、乙
【分析】
根据方差的定义,方差越小数据越稳定.
【详解】
解:∵s甲2=0.01,s乙2=0.009,s丙2=0.0093,
∴s乙2<s丙2<s甲2,
∴甲、乙、丙三位同学中成绩最稳定的是乙.
故答案为:乙.
【点睛】
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
三、解答题
1、(1)100名;(2)图见解析;(3);(4)700.
【分析】
(1)根据等级的条形统计图和扇形统计图的信息即可得;
(2)根据(1)的结果,求出等级的学生人数,再补全条形统计图即可;
(3)利用乘以等级所占的百分比即可得;
(4)利用2000乘以等级所占的百分比即可得.
【详解】
解:(1)抽取调查的学生总人数为(名),
答:共抽取了100名学生进行调查;
(2)等级的人数为(名),
则补全条形统计图如下:
(3)图乙中等级所对应的扇形圆心角的度数为,
答:图乙中等级所对应的扇形圆心角的度数;
(4)(名),
答:估计有700名学生获得等级的评价.
【点睛】
本题考查了条形统计图和扇形统计图的信息关联,熟练掌握统计调查的相关知识是解题关键.
2、(1)224,177,170,补全条形统计图见解析;(2)甲食堂较好,理由见解析;(3)甲食堂每天中午大约准备844名同学的午餐.
【分析】
(1)利用中位数,众数,极差的定义分别求解,求出乙食堂的“B组”的频数才能补全频数分布直方图;
(2)从平均数的角度比较得出结论;
(3)用样本估算总体即可.
【详解】
解:(1)甲食堂20天的所有人数中位数是第10、11个数据,
∴a=224,
177人的有3天,天数最多,∴b=177,
乙食堂20天的人数数据中最少人数为120人,A等级的数据为278,290,260,
∴c=290-120=170;
∵20-3-7-4=6,
∴补全乙食堂的人数数据条形统计图如图:
故答案为:224,177,170;
(2)甲食堂较好,理由:甲食堂就餐人数的平均数比乙食堂的高;
(3)1600×=844(名),
故北关中学甲食堂每天中午大约准备844名同学的午餐.
【点睛】
本题考查中位数、众数、极差以及频数分布直方图,理解中位数、众数、极差的意义,掌握频数分布直方图的意义是正确解答的关键.
3、(1)60;(2)补全统计图见详解;(3);(4)估计该校表示“很喜欢”的A类的学生有260人.
【分析】
(1)C类学生占比25%,根据条形统计图的数据可得C类学生有15人,由此计算总人数即可;
(2)计算得出D类学生人数,根据D类学生人数补全条形统计图即可;
(3)根据前面的结论,计算出B类人数占总调查人数的比值,将计算结果乘即可得出扇形圆心角的度数;
(4)利用调查样本所占的百分比估计总体学生数即可.
【详解】
解:(1)此次调查学生总数:(人),
故答案为:60;
(2)D类人数为:(人),
补全条形统计图,如图所示,
(3)扇形统计图中,B类所对应的扇形圆心角的大小为:,
故答案为:;
(4)(人).
∴估计该校表示“很喜欢”的A类的学生有260人.
【点睛】
本题考查了条形统计图和扇形统计图的信息关联,求扇形统计图的圆心角,画条形统计图,由样本百分比估计总体的数量,从不同的统计图中获取需要的信息是解题关键.
4、(1)见解析;(2)960只
【分析】
(1)先根据D组的频数和占比求出抽取兔子的数量,然后求出C组兔子的数量,最后补全统计图即可;
(2)先求出样本中这批兔子中质量不小于1.7kg的百分比,然后估计总体即可.
【详解】
解:(1)抽取兔子的数量是,
则质量在“C”部分的兔子数量是(只).
补全频数分布直方图如下:
(2)由题意得:这批兔子中质量不小于1.7kg的大约有(只).
【点睛】
本题主要考查了条形统计图与扇形统计图信息相关联,用样本估计总体,补全条形统计图,解题的关键在于能够正确理解题目所示的统计图.
5、(1)40 (2)a=6,b=,频数分布直方图见解析(3)72°
【分析】
(1)根据体育锻炼时间“3≤t<4”频数10,占学生总人数的百分比是25%,可得答案;
(2)由(1)的结果学生总人数可求a,由学生总人数和频数4,可求b;
(3)根据体育锻炼时间“5≤t<6”占学生总人数的百分比20%,即可得答案.
【详解】
解:(1)∵体育锻炼时间“3≤t<4”频数10,百分比是25%,
∴学生总人数为10÷25%=40;
(2)∵学生总人数为40,
∴a=40-4-10-8-12=6,b= ;
∴频数分布直方图为下图:
(3)体育锻炼时间“5≤t<6” 占学生总人数的百分比为20%,
∴对应的扇形圆心角的度数= .
【点睛】
本题考查了数据的收集与整理,做题的关键是掌握由频数和对应的百分比会求总数,频数和总数会求扇形的圆心角.
初中数学北京课改版八年级下册第十七章 方差与频数分布综合与测试习题: 这是一份初中数学北京课改版八年级下册第十七章 方差与频数分布综合与测试习题,共20页。试卷主要包含了篮球队5名场上队员的身高,新型冠状病毒肺炎,为考察甲等内容,欢迎下载使用。
数学北京课改版第十七章 方差与频数分布综合与测试课后复习题: 这是一份数学北京课改版第十七章 方差与频数分布综合与测试课后复习题,共21页。
初中数学北京课改版八年级下册第十七章 方差与频数分布综合与测试一课一练: 这是一份初中数学北京课改版八年级下册第十七章 方差与频数分布综合与测试一课一练,共21页。