2021学年第十七章 方差与频数分布综合与测试课后练习题

京改版八年级数学下册第十七章方差与频数分布综合训练

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、在一次射击训练中，甲、乙两人各射击10次，两人10次射击成绩的平均数均是9.1环，方差分别是＝1.2，＝1.1，则关于甲、乙两人在这次射击训练中成绩稳定的描述正确的是（    ）

A．乙比甲稳定 B．甲比乙稳定

C．甲和乙一样稳定 D．甲、乙稳定性没法对比

2、某企业为了解员工给灾区“爱心捐款”的情况，随机抽取部分员工的捐款金额整理绘制成如图所示的直方图，根据图中信息，下列结论错误的是（　　）

A．样本中位数是200元

B．样本容量是20

C．该企业员工捐款金额的极差是450元

D．该企业员工最大捐款金额是500元

3、为了解某社区居民的用电情况，随机对该社区15户居民进行调查，下表是这15户居民2020年4月份用电量的调查结果：关于这15户居民月用电量（单位：度），下列说法错误的是（　　）

A．平均数是43.25 B．众数是30

C．方差是82.4 D．中位数是42

4、已知两组数据x1，x2，x3和x1+1，x2+1，x3+1，则这两组数据没有改变大小的统计量是（　　）

A．平均数 B．中位数 C．众数 D．方差

5、在一个样本中，40个数据分别落在5个小组内，第1，2，3，5小组的频数分别是6，5，15，7，则第4小组的频数是（   ）

A．7 B．8 C．9 D．10

6、下列说法中正确的是（    ）．

A．想了解某河段的水质，宜采用全面调查 B．想了解某种饮料中含色素的情况，宜采用抽样调查

C．数据1，1，2，2，3的众数是3 D．一组数据的波动越大，方差越小

7、小明抛一枚硬币100次，其中有60次正面朝上，则反面朝上的频率是（　　）

A．0.6 B．6 C．0.4 D．4

8、已知一组数据有80个，其中最大值为140，最小值为40，取组距为10，则可分成（    ）．

A．11组 B．9组 C．8组 D．10组

9、2020年某果园随机从甲、乙、丙、丁四个品种的苹果树上各采摘了10棵．每棵产量的平均数（单位：千克）及方差s2（单位：千克2）如下表所示：

今年准备从这四个品种中选出一种产量既高又稳定的苹果树进行种植．应选的品种是（    ）

A．甲 B．乙 C．丙 D．丁

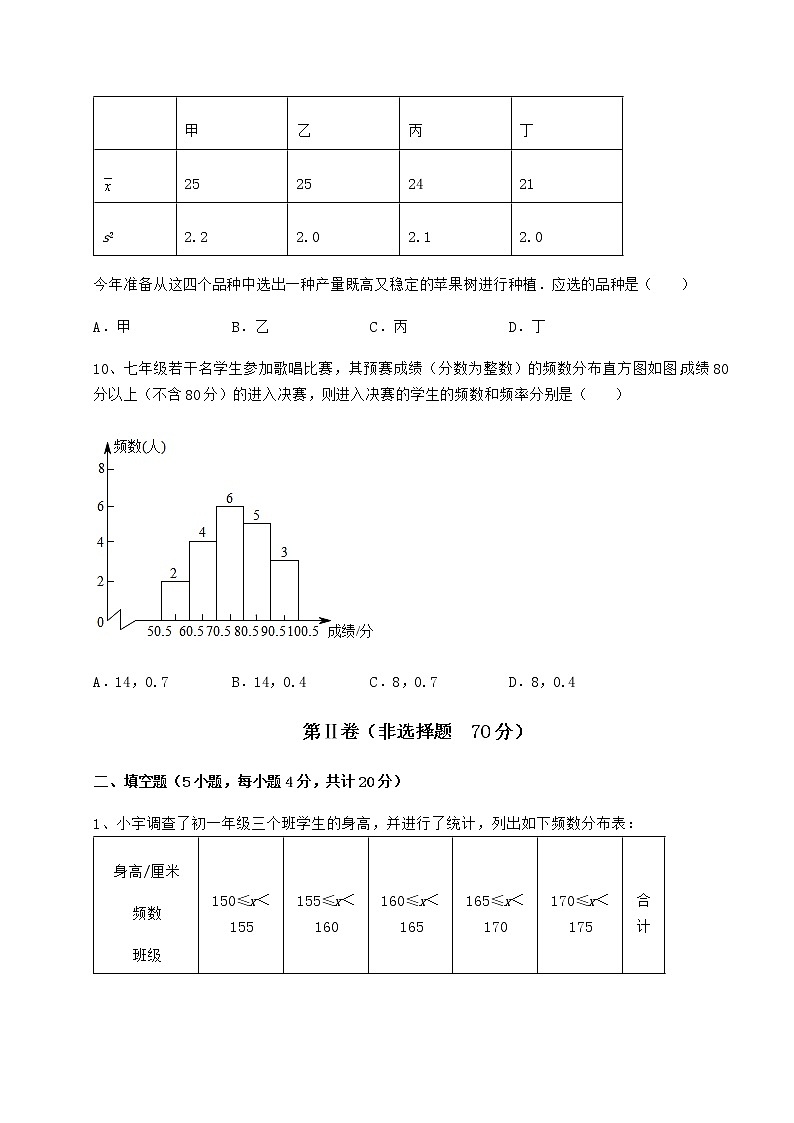
10、七年级若干名学生参加歌唱比赛，其预赛成绩（分数为整数）的频数分布直方图如图，成绩80分以上（不含80分）的进入决赛，则进入决赛的学生的频数和频率分别是（    ）

A．14，0.7 B．14，0.4 C．8，0.7 D．8，0.4

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、小宇调查了初一年级三个班学生的身高，并进行了统计，列出如下频数分布表：

若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示，不考虑其他因素的影响，则 _____（填“1班”，“2班”或“3班”）的可供挑选的空间最大．

2、已知一组数据x1，x2，x3，方差是2，那么另一组数据2x1﹣4，2x2﹣4，2x3﹣4的方差是 ______________．

3、已知一组数据a，b，c的方差为4，那么数据3a﹣2，3b﹣2，3c﹣2的方差是_____．

4、跳远运动员李强在一次训练中，先跳了6次的成绩如下：7.6，7.8，7.7，7.8，8.0，7.9（单位：m）．这六次成绩的平均数为7.8，方差为．如果李强再跳两次，成绩分别为7.6，8.0，则李强这8次跳远成绩与前6次的成绩相比较，其方差 _____．（填“变大”、“不变”或“变小”）

5、若一组数据，，，…，的方差为4.5，则另一组数据2，2，2，…，2的方差为____．

三、解答题（5小题，每小题10分，共计50分）

1、在一组数据中，各数据与它们的平均数的差的绝对值的平均数，即叫做这组数据的“平均差”，“平均差”也能描述一组数据的离散程度，“平均差”越大，说明数据的离散程度越大．

（1）分别计算下列两组数据的“平均差”，并根据计算结果比较这两组数据的稳定性；

甲：9，11，8，12，7，13，6，14，10，10．

乙：8，9，10，11，7，12，9，11，10，13．

（2）分别计算甲、乙两组数据的方差，并根据计算结果比较这两组数据的稳定性．

2、在精准扶贫的政策下，某贫困户在当地政府的支持和帮助下办起了养殖业，经过一段时间的精心饲养，总量为6000只的一批兔子达到了出售标准，现从这批兔中随机选择部分进行称重，将得到的数据用下列统计图表示（频数分布直方图每组含前一个边界值，不含后一个边界值）．根据以上信息，解答下列问题：

（1）补全图中的频数分布直方图；

（2）估计这批兔子中质量不小于1.7kg的有多少只．

3、随着经济的发展，我们身边的环境受到很大的影响，为了保护环境加强环保教育，某市实验中学组织500名学生参加义务收集废旧电池的活动，下面随机抽取50名学生对收集的废旧电池数量进行统计：

（1）这50名学生平均每人收集废旧电池多少节？

（2）这组废旧电池节数的中位数，众数分别是多少？

（3）根据统计发现，本次收集的各种废旧电池的数量比为：手机电池：7号电池：5号电池：1号电池＝2：3：4：3，根据资料显示，各种电池1节能污染水的量之比为：手机电池：7号电池：5号电池：1号电池＝6：1：2：3，且1节7号电池能使500吨的水受到污染，那么通过本次活动可减少受浸染的水多少吨？

4、某县教育局组织了一次经典诵读比赛，中学组有两队各10人的比赛成绩如下表：

（1）甲队成绩的中位数是          分，乙队成绩的众数是          分；

（2）计算乙队的平均成绩；

（3）如果要从两个队中选择一对参加市级比赛，你认为安排哪个队更容易获奖．

5、某学校从九年级同学中任意选取40人，随机分成甲、乙两个小组进行“引体向上”体能测试，根据测试成绩绘制出统计表和如图所示的统计图（成绩均为整数，满分为10分）

甲组成绩统计表：

乙组成绩统计图

根据上面的信息，解答下列问题：

（1）甲组的平均成绩为______分，______，甲组成绩的中位数是______，乙组成绩的众数是______；

（2）若已经计算出甲组成绩方差为0.81，求出乙组成绩的方差，并判断哪个小组的成绩更加稳定？

-参考答案-

一、单选题

1、A

【分析】

根据方差的性质解答．

【详解】

解：∵甲乙两人的方差分别是＝1.2，＝1.1，

∴乙比甲稳定，

故选：A．

【点睛】

此题考查了方差的性质：方差越小越稳定．

2、A

【详解】

解：A、共2+8+5+4+1=20人，中位数为10和11的平均数，故中位数为150元，故选项A不正确；

B、共20人，样本容量为20，故选项B正确；

C、极差为500﹣50=450元，故选项C正确；

D、该企业员工最大捐款金额是500元，故选项D正确．

故选：A ．

【点睛】

本题考查脂肪性获取信息，中位数，样本容量，极差，掌握相关概念是解题关键．

3、A

【分析】

根据表格中的数据，求出平均数，中位数，众数，方差，即可做出判断．

【详解】

解：15户居民2015年4月份用电量为30，30，30，30，30，42，42，42，50，50，50，51，51，51，51，

平均数为×（30+30+30+30+30+42+42+42+50+50+50+51+51+51+51）＝42，

中位数为42；

众数为30，

方差为 ×[5×（30﹣42）2+3×（42﹣42）2+3×（50﹣42）2+4×（51﹣42）2]＝82.4．

故B、C、D正确．

故选：A．

【点睛】

本题考查的是平均数，中位数，众数，方差，熟练掌握平均数，中位数，众数，方差的定义是解题关键．

4、D

【分析】

由平均数，中位数，众数，方差的定义逐项判断即可．

【详解】

A．第一组数据平均数为，第二组数据平均数为，有改变，故该选项不符合题意．

B．由于不知道各数据具体数值，故无法比较中位数是否变化，故该选项不符合题意．

C．由于不知道各数据具体数值，故无法比较众数是否变化，故该选项不符合题意．

D．由第二组数据是把第一组数据都加1得到的一组新数据，平均数与差的平方的平均数没有改变，波动没变，所以方差不变，故该选项符合题意．

故选：D．

【点睛】

本题考查平均数，中位数，众数，方差的定义．掌握方差是用来衡量一组数据波动大小的量，数据的波动情况不变，方差不会变是解答本题的关键．

5、A

【分析】

每组的数据个数就是每组的频数，40减去第1，2，3，5小组数据的个数就是第4组的频数．

【详解】

解：第4小组的频数是40−（6＋5＋15＋7）＝7，
故选：A．

【点睛】

本题考查频数和频率的知识，注意掌握每个小组的频数等于数据总数减去其余小组的频数，即各小组频数之和等于数据总和．

6、B

【分析】

分别根据全面调查和抽样调查的定义，众数的定义，方差的性质进行判断即可．

【详解】

解：A、想了解某河段的水质，宜采用抽样调查，故本选项不正确，不符合题意；

B、想了解某种饮料中含色素的情况，宜采用抽样调查，故本选项正确，符合题意；

C、数据1，1，2，2，3的众数是1和2，故本选项不正确，不符合题意；

D、一组数据的波动越大，方差越大，故本选项不正确，不符合题意；

故选：B．

【点睛】

本题考查了全面调查和抽样调查，方差，众数，选择全面调查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行全面调查、全面调查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用全面调查．一组数据中出现次数最多的数据叫做众数．方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．

7、C

【分析】

先求出反面朝上的频数，然后根据频率=频数÷总数求解即可

【详解】

解：∵小明抛一枚硬币100次，其中有60次正面朝上，

∴小明抛一枚硬币100次，其中有40次反面朝上，

∴反面朝上的频率=40÷100=0.4，

故选C．

【点睛】

本题主要考查了根据频数求频率，解题的关键在于能够熟练掌握频率=频数÷总数．

8、A

【分析】

据组数=（最大值-最小值）÷组距计算即可得解，注意小数部分要进位．

【详解】

解：由组数=（最大值-最小值）÷组距可得：

组数=（140-40）÷10+1=11，

故选择：A

【点睛】

本题考查的是组数的计算，属于基础题，只要根据组数的定义“数据分成的组的个数称为组数”来解即可．

9、B

【分析】

首先比较平均数，平均数较高的是甲和乙，进而根据方差比较选出方差较小的即可．

【详解】

根据表格可知甲、乙的平均数较高，则表示产量高，比较甲、乙的方差，乙的方差比甲小，则乙品种的苹果树产量高又稳定，

故选B．

【点睛】

本题考查了方差的意义，若两组数据的平均数相同，则方差小的更稳定，理解方差的意义是解题的关键．

10、D

【分析】

根据题意，成绩分式为整数，则大于80.5的频数为5+3=8，根据频率等于频数除以总数即可求得

【详解】

依题意，成绩分式为整数，则大于80.5的频数为5+3=8，

学生总数为．

则频率为．

故选D．

【点睛】

本题考查了频数分布直方图，根据题意求频数和频率，读懂题意以及统计图是解题的关键．

二、填空题

1、1班

【分析】

根据各个班身高在160cm和170cm之间同学的人数，进行判断即可．

【详解】

解：身高在160cm和170cm之间同学人数：1班26人，2班13人，3班18人，因此可挑选空间最大的是1班，

故答案为：1班．

【点睛】

此题考查频数分布表的表示方法，从表格中获取数据和数据之间的关系是正确判断的前提．

2、8

【分析】

设这组数据，，的平均数为，则另一组数据，，的平均数为，因为数据，，的方差为，所以数据，，的方差为，进行计算即可得．

【详解】

解：设这组数据，，的平均数为，则另一组数据，，的平均数为，

∵数据，，的方差为：

，

∴数据，，的方差为：

=

=

=

=8

故答案为：8．

【点睛】

本题考查了方差，解题的关键是掌握方差的公式．

3、36

【分析】

根据“当数据都乘以一个数（或除以一个数）时，平均数也乘以或除以这个数，方差变为这个数的平方倍”求解可得．

【详解】

解：∵数据a，b，c的方差为4，

∴数据3a﹣2，3b﹣2，3c﹣2的方差32×4＝36，

故答案为：36．

【点睛】

本题考查了方差的定义．当数据都加上一个数（或减去一个数）时，平均数也加或减这个数，方差不变，即数据的波动情况不变；当数据都乘以一个数（或除以一个数）时，平均数也乘以或除以这个数，方差变为这个数的平方倍．

4、变大

【分析】

先由平均数的公式计算出李强第二次的平均数，再根据方差的公式进行计算，然后比较即可得出答案．

【详解】

解：∵李强再跳两次，成绩分别为7.6，8.0，

∴这组数据的平均数是，

∴这8次跳远成绩的方差是：

∵0.0225＞，

∴方差变大；

故答案为：变大．

【点睛】

本题主要考查了平均数的计算和方差的计算，熟练掌握平均数和方差的计算是解答此题的关键．

5、18

【分析】

根据方差的计算公式计算即可．

【详解】

设，，，…，的平均数为，则2，2，2，…，2的平均数为2，

∵数据，，，…，的方差为4.5，

∴=，

∴

=

=

=18，

故答案为：18．

【点睛】

本题考查了方差的计算，熟练掌握方差的计算公式是解题的关键．

三、解答题

1、（1）T甲=2，T乙=1.4，乙组数据更稳定；（2）=6，=3，乙组数据更稳定

【分析】

（1）先求出甲乙两组的平均数，再利用平均差公式求出甲乙两组的平均差，再比较大小即可；

（2）根据方差公式求甲乙两组的方差，再比较大小即可．

【详解】

解：（1）∵，

∴…，

∵，

∴…，

∴,

∴乙组数据更稳定；

（2）∵，

，

，

∴乙组数据更稳定．

【点睛】

本题考查平均数，新定义平均差，方差，掌握平均数，新定义平均差，方差是解题关键．

2、（1）见解析；（2）960只

【分析】

（1）先根据D组的频数和占比求出抽取兔子的数量，然后求出C组兔子的数量，最后补全统计图即可；

（2）先求出样本中这批兔子中质量不小于1.7kg的百分比，然后估计总体即可．

【详解】

解：（1）抽取兔子的数量是，

则质量在“C”部分的兔子数量是（只）．

补全频数分布直方图如下：

（2）由题意得：这批兔子中质量不小于1.7kg的大约有（只）．

【点睛】

本题主要考查了条形统计图与扇形统计图信息相关联，用样本估计总体，补全条形统计图，解题的关键在于能够正确理解题目所示的统计图．

3、（1）4.8节；（2）众数为4个，中位数为4.5节；（3）本次活动可减少受浸染的水3200000吨．

【分析】

（1）求出50名学生收集废旧电池的总数，再求平均数即可；

（2）从统计表格即可求得众数为5，然后按从大到小给所有数据排序，求出中位数即可；

（3）先求出这些电池可污染的水的数量即可解决问题．

【详解】

解：（1）50名学生平均每人收集废旧电池的节数=（10×3+15×4+12×5+7×6+6×8）÷50=4.8（节）；

（2）从统计表格得，众数为4节；

由于收集3节和4节电池的人数有25个人，收集5节的人有12人，所以中位数=（4+5）÷2=4.5（节）；

（3）样本中电池总数4.8×50=240，

由于本次收集的各种电池的数量比为：手机电池：7号电池：5号电池：1号电池＝2：3：4：3，

故可得出手机电池、7号电池、5号电池、1号电池与总数的比值分别为：

，，，，即，，，，

由于各种电池1节能污染水的量的比为：手机电池：7号电池：5号电池：1号电池＝6：1：2：3，且1节7号电池能使500吨的水受到污染，故可得手机电池、5号电池、1号电池一节分别能污染水的吨数为500×6，500×2，500×3，

故在50名学生收集的废电池可少受污染水的吨数为

=320000（吨）

320000÷50×500=3200000吨，

答：本次活动可减少受浸染的水3200000吨．

【点睛】

本题考查了从统计图中获取信息的能力；对平均数、中位数和众数等概念的掌握程度．同时通过此题倡导学生参加义务收集废旧电池活动中来．

4、（1）9.5，10；（2）9；（3）甲，乙的平均分均为9分，但是甲的方差为1.4，乙的方差为1，所以乙队的成绩更加稳定，选择乙

【分析】

（1）先将甲队的成绩按从小到大的顺序排列，可得位于第5位和第6位的分别为9和10 ，可得甲队成绩的中位数是9.5分，再由乙队成绩中10出现的次数最多，可得乙队成绩的众数是10分；

（2）利用乙队成绩的总和除以10，即可求解；

（3）分别两队的平均成绩和方差，即可求解．

【详解】

解：（1）将甲队的成绩按从小到大的顺序排列为：7、7、8、9、9、10、10、10、10、10，位于第5位和第6位的分别为9和10 ，

∴甲队成绩的中位数是 分，

∵乙队成绩中10出现了4次，出现的次数最多，

∴乙队成绩的众数是10分；

（2）乙队的平均成绩为 分；

（3）甲队的平均成绩为 分，

甲队成绩的方差为

乙队成绩的方差为，

∴甲，乙的平均分均为9分，但是甲的方差为1.4，乙的方差为1，

∴乙队的成绩更加稳定，选择乙．

【点睛】

本题主要考查了求一组数据的中位数，众数，平均数，利用方差做决策，熟练掌握一组数据中位于正中间的一个数或两个数的平均数是中位数；出现次数最多的数是众数；平均数等于数据的总和除以个数；方差越小，越稳定是解题的关键．

5、（1）8.7，3，8.5，8；（2）乙组成绩的方差为0.75，乙组的成绩更加稳定．

【分析】

（1）根据数据平均数的计算方法可得平均数；用总人数减去其他成绩的人数即为m的值；根据中位数（一组数据从小到大排序后最中间的数）和众数（一组数据中出现次数最多的）的定义即可确定甲组成绩的中位数，乙组成绩的众数；

（2）先求出乙组数据的平均数，再根据方差公式求出乙组方差，然后进行比较，即可得出答案．

【详解】

解：（1）平均成绩为：，

，

甲组成绩一共有20人，从小到大最中间为8和9，则中位数为，

乙组成绩中出现次数最多的为8，则众数为8，

故答案为：8.7,3,8.5,8；

（2），

，

，

∴，

∴乙组的成绩更加稳定．

【点睛】

题目主要考查平均数、中位数、众数的定义、方差的算法及数据的稳定性判断，理解定义及方差的算法是解题关键．