高中数学人教A版 (2019)必修 第一册5.3 诱导公式教案配套课件ppt

这是一份高中数学人教A版 (2019)必修 第一册5.3 诱导公式教案配套课件ppt，共34页。PPT课件主要包含了正弦函数，余弦函数，答案CD等内容，欢迎下载使用。

(一)教材梳理填空1．诱导公式五和公式六：
(二)基本知能小试1．判断正误(1)诱导公式五、六中的角α只能是锐角．(　　)(2)sin(90°＋α)＝－cs α.(　　)(3)cs(270＋30°)＝sin 30°.(　　)答案：(1)×　(2)×　(3)√
3．sin 95°＋cs 175°的值为(　　)A．sin 5°　　B．cs 5° C．0　　D．2sin 5°解析：sin 95°＋cs 175°＝sin(90°＋5°)＋cs(180°－5°)＝cs 5°－cs 5°＝0.答案：C4．计算：sin211°＋sin279°＝________.解析：sin211°＋sin279°＝sin211°＋cs211°＝1.答案：1
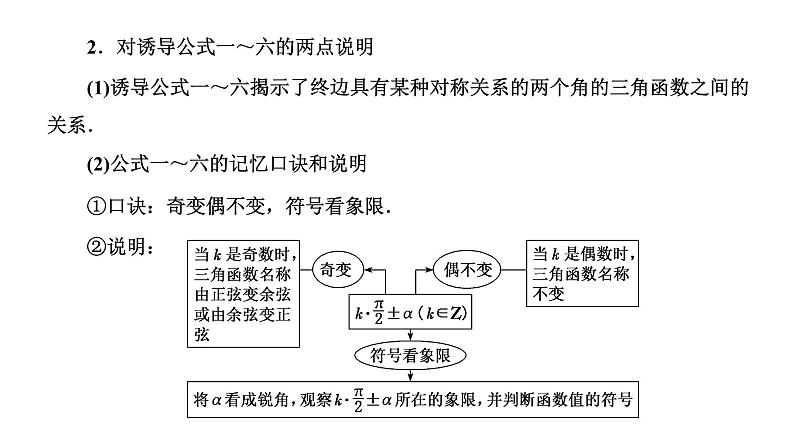
2．对诱导公式一～六的两点说明(1)诱导公式一～六揭示了终边具有某种对称关系的两个角的三角函数之间的关系．(2)公式一～六的记忆口诀和说明①口诀：奇变偶不变，符号看象限．②说明：
[方法技巧]1.求值问题中角的转化方法2．用诱导公式进行化简的要求三角函数的化简是表达式经过某种变形使结果尽可能的简单：(1)化简后项数尽可能地少．(2)函数的种类尽可能地少．(3)分母不含三角函数的符号．(4)能求值的一定要求值．(5)含有较高次数的三角函数式，多用因式分解、约分等．　　
[方法技巧]证明等式的常用方法利用诱导公式证明等式问题，关键在于公式的灵活应用，其证明的常用方法有：(1)从一边开始，使得它等于另一边，一般由繁到简．(2)左右归一法：即证明左右两边都等于同一个式子．(3)针对题设与结论间的差异，有针对性地进行变形，以消除差异．　　
[方法技巧]诱导公式综合应用要“三看”一看角：①化大为小；②看角与角间的联系，可通过相加、相减分析两角的关系．二看函数名称：一般是弦切互化．三看式子结构：通过分析式子，选择合适的方法，如分式可对分子、分母同乘一个式子变形．　　
二、应用性——强调学以致用2. 如图，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在(0,1)，此时圆上一点P的位置在(0,0)，圆在x轴上沿正向滚动．当圆滚动到圆心位于(2,1)时，求P的坐标．[析题建模]
三、创新性——强调创新意识和创新思维3．(1)已知f(sin x)＝cs x，求f(cs x)；(2)已知f(sin x)＝cs 17x，求f(cs x)；(3)请同学们试探究以下式子成立的条件．①对于怎样的整数k，能由f(sin x)＝cs kx推出f(cs x)＝sin kx成立？说明理由．②对于怎样的整数k，能由f(cs x)＝cs kx推出f(sin x)＝sin kx成立？说明理由．③对于怎样的整数k，能由f(sin x)＝sin kx推出f(cs x)＝cs kx成立？说明理由．
“课时跟踪检测”见“课时跟踪检测（三十七）” (单击进入电子文档)