数学第2章 圆2.5 直线与圆的位置关系优质课件ppt

这是一份数学第2章 圆2.5 直线与圆的位置关系优质课件ppt

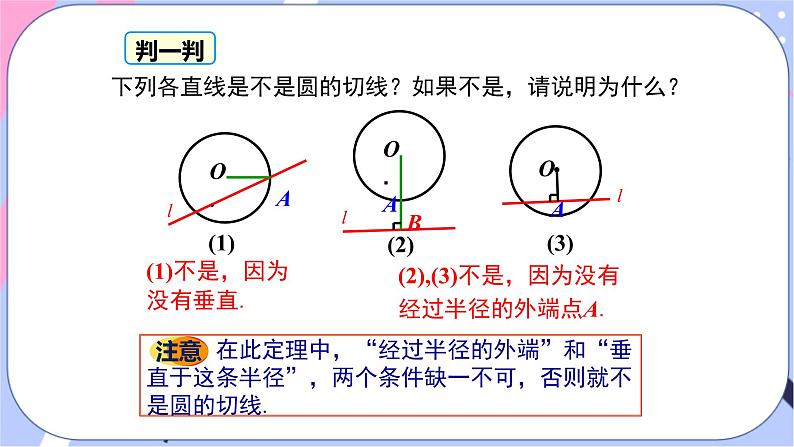
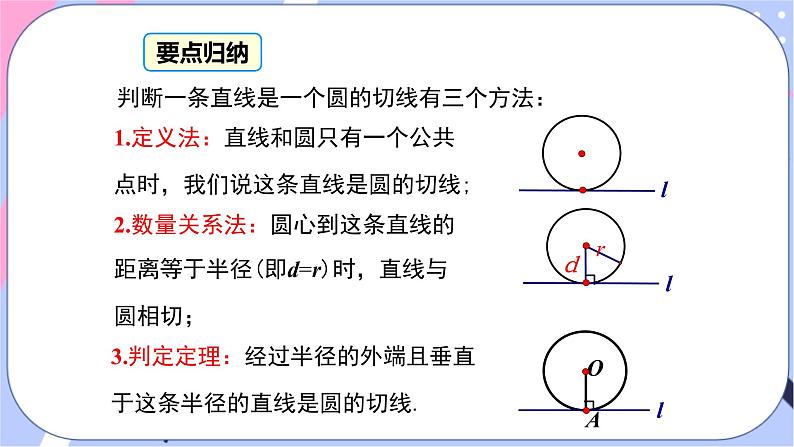
2.5 直线和圆的位置关系第2章 圆第1课时 切线的判定 2.5.2 圆的切线 1.理解和掌握圆的切线的判定定理；(重点)2.能运用圆的切线的判定定理进行相关的计算和证明．(难点)情境引入转动雨伞时飞出的雨滴，用砂轮磨刀时擦出的火花，都是沿着什么方向飞出的？都是沿切线方向飞出的. 生活中常看到切线的实例，如何判断一条直线是否为切线呢？学完这节课，你就都会明白.讲授新课问题1 如图，OA是⊙O的半径， 经过OA 的外端点A， 作一条直线l⊥OA，圆心O 到直线l 的距离是多少？ 直线l 和⊙O有怎样的位置关系？合作探究ll经过半径的外端并且垂直于这条半径的直线是圆的切线.OA为⊙O的半径BC ⊥ OA于ABC为⊙O的切线BC知识要点下列各直线是不是圆的切线？如果不是，请说明为什么？(1)不是，因为没有垂直.(2),(3)不是，因为没有经过半径的外端点A.判一判判断一条直线是一个圆的切线有三个方法：1.定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线;2.数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；3.判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线.要点归纳用三角尺过圆上一点画圆的切线.做一做（2） 过点P 沿着三角尺的另一条直角边画直线l，则l 就是所要画的切线.如图所示.如下图所示，已知⊙O 上一点P，过点P 画⊙O 的切线．画法：（1）连接OP，将三角尺的直角顶点放在点P处， 并使一直角边与半径OP 重合；例1 已知：如图所示，AD是圆O的直径，直线BC经过点D，并且AB=AC，∠BAD=∠CAD. 求证：直线BC是圆O的切线.证明 因为 AB=AC，∠BAD=∠CAD，所以 AD⊥BC.又因为OD是圆O的半径，且BC经过点D，所以直线BC是圆O的切线.例1变式 已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB.求证：直线AB是⊙O的切线.OBAC分析：由于AB过⊙O上的点C，所以连接OC，只要证明AB⊥OC即可. 证明：连接OC(如图). ∵ OA＝OB,CA＝CB, ∴ OC是等腰三角形OAB底边AB上的中线.　 ∴ AB⊥OC. ∵ OC是⊙O的半径, ∴ AB是⊙O的切线. 1.如图,△ABC 中，AB ＝AC ，O 是BC中点，E为⊙O 上一点，且OE ⊥ AB.求证：AC 是⊙O 的切线．BOCEA针对训练证明：连接OA, 过O 作OF ⊥AC.∵△ABC 中，AB ＝AC ，　　O 是BC 中点．∴AO 平分∠BAC，FBOCEA∴OE ＝OF.∵OE 是⊙O 半径，OF ＝OE，OF ⊥ AC.∴AC 是⊙O 的切线．又OE ⊥AB ，OF⊥AC.(1)证明：连接OC，BC.∵FC＝CB，∴∠DAC＝∠BAC.∵CD⊥AF，∴∠ADC＝90°.∵AB是直径，∴∠ACB＝90°.∴∠ACD＝∠B.︵︵∵BO＝OC，∴∠OCB＝∠OBC.∵∠ACO＋∠OCB＝90°，∠OCB＝∠OBC，∠ACD＝∠ABC，∴∠ACO＋∠ACD＝90°，即OC⊥CD.又∵OC是⊙O的半径，∴CD是⊙O的切线；(2)若CD＝ ，求⊙O的半径．(2)解：∵AF＝FC＝CB，∴∠DAC＝∠BAC＝30°.∵CD⊥AF，CD＝ ，∴AC＝ .在Rt△ABC中，∠BAC＝30°，AC＝ ，∴BC＝4，AB＝8，∴⊙O的半径为4.︵︵︵(1) 已明确直线和圆有公共点，连结圆心和公共点，即半径，再证直线与半径垂直.简记“有交点，连半径,证垂直”;(2) 不明确直线和圆有公共点，过圆心作直线的垂线，再证圆心到直线的距离等于半径.简记“无交点，作垂直,证半径”.证切线时辅助线的添加方法 1.判断下列命题是否正确. ⑴ 经过半径外端的直线是圆的切线. （ ） ⑵ 垂直于半径的直线是圆的切线. （ ） ⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线. （ ） ⑷ 和圆只有一个公共点的直线是圆的切线. （ ） ⑸ 过直径一端点且垂直于直径的直线是圆的切线. （ ） 当堂练习××√√√2.如图所示，A是☉O上一点，且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 .相切3.如图，O为正方形ABCD的对角线AC上一点，以O为圆心，OA的长为半径的⊙O与BC相切于点M.求证：CD与⊙O相切．证明：连接OM，过点O作ON⊥CD于点N，∵⊙O与BC相切于点M，∴OM⊥BC，又∵ON⊥CD，O为正方形ABCD对角线AC上一点，∴OM＝ON，∴CD与⊙O相切．证明：连接OP. ∵AB=AC,∴∠B=∠C. ∵OB=OP，∴∠B=∠OPB， ∴∠OPB=∠C. ∴OP∥AC. ∵PE⊥AC， ∴PE⊥OP. ∴PE为☉O的切线.4.如图,△ABC中，AB=AC，以AB为直径的☉O交边BC于P， PE⊥AC于E. 求证:PE是☉O的切线.OABCEP5.已知：△ABC内接于☉O，过点A作直线EF.（1）如图1，AB为直径，要使EF为☉O的切线，还需添加的条件是（只需写出两种情况）： ① _________ ；② _____________ .（2）如图2，AB是非直径的弦，∠CAE=∠B，求证：EF是☉O的切线.BA⊥EF∠CAE=∠B证明：连接AO并延长交☉O于D,连接CD,则AD为☉O的直径.∴ ∠D+ ∠DAC=90 °,∵ ∠D与∠B同对 ,∴ ∠D= ∠B,又∵ ∠CAE= ∠B,∴ ∠D= ∠CAE,∴ ∠DAC+ ∠EAC=90°,∴EF是☉O的切线.D6.如图，AB为⊙O的直径，C为⊙O上一点，CD⊥AB于点D．P为AB延长线上一点，∠PCD=2∠BAC．（1）求证：CP为⊙O的切线；（1）证明：连接OC，如图1，∵OA=OC，∴∠BAC=∠ACO，∴∠POC=2∠BAC.∵∠PCD=2∠BAC，∠POC=2∠BAC，∴∠POC=∠PCD，∵CD⊥AB于点D，∴∠ODC=90°．∴∠POC+∠OCD=90°．∴∠PCD+∠OCD=90°．∴∠OCP=90°．∴半径OC⊥CP．∴CP为⊙O的切线．（2）解：①设⊙O的半径为r．在Rt△OCP中，OC2+CP2=OP2，∵BP=1，CP= ．∴r2+（ ）2=（r+1）2，解得r=2．∴⊙O的半径为2． ②若M为AC上一动点，求OM+DM的最小值．②∵∠OCP=∠ODC=90°，∠COD=∠POC，∴△COP∽△DOC，∴ ，即 ，∴CD= ，如图，作点O点关于AC的对称点E，连接AE，EC，ED，ED交AC于点M，此时OM+DM的值最小，为ED，∵AC垂直平分OE，∴AE=AO，∴∠OAC=∠EAC，∵OA=OC，∴∠OAC=∠OCA，∴∠EAC=∠OCA，∴AE∥OC，∵OA=AE=OC=2，∴四边形AOCE是菱形，∴EC=2，∠ECD=90°，在Rt△ECD中，EC=2，CD= ，∴ED2=CE2+CD2= ．∵OM+DM的最小值为 ．课堂小结切线的判定方法定义法数量关系法判定定理1个公共点，则相切d=r，则相切经过圆的半径的外端且垂直于这条半径的直线是圆的切线.证切线时常用辅助线添加方法： ①有公共点，连半径，证垂直；②无公共点，作垂直，证半径.