四川省南充市阆中中学2020-2021学年高二数学上学期期中试题理仁智班（含答案）.

四川省南充市阆中中学2020-2021学年高二数学上学期期中试题 理（仁智班）

一．选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只

    有一项是符合题目要求的)

1. 若直线与直线平行，则它们之间的距离为

   A.     B.    C.    D.

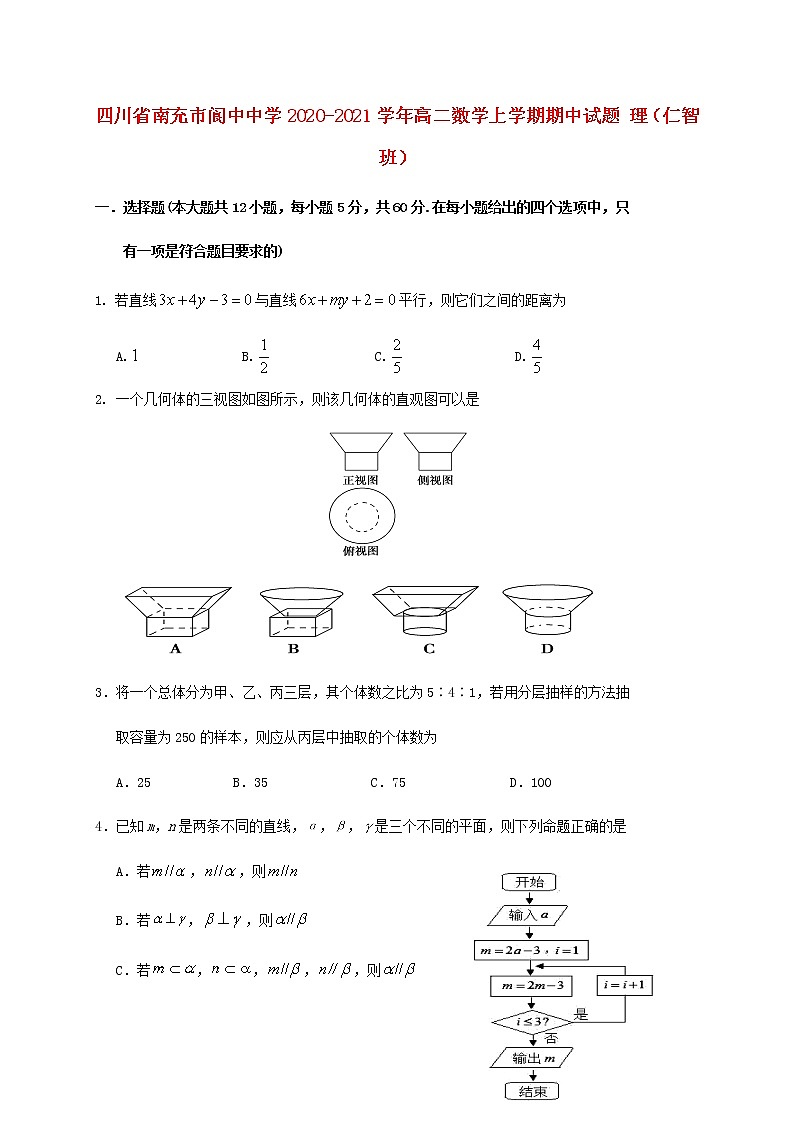
2. 一个几何体的三视图如图所示，则该几何体的直观图可以是 　　

3．将一个总体分为甲、乙、丙三层，其个体数之比为5∶4∶1，若用分层抽样的方法抽

   取容量为250的样本，则应从丙层中抽取的个体数为

   A．25 B．35 C．75 D．100

4．已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是

   A．若，，则        

   B．若，，则

   C．若，，，，则

   D．若，，且，则

5.《算法统宗》是我国古代数学名著，由明代数学家程大位

   所著，该著作完善了珠算口诀，确立了算盘用法，完成

   了由筹算到珠算的转变，对我国民间普及珠算起到了重

   要的作用.如果所示的程序框图的算法思路源于该著作

   中的“李白沽酒”问题.执行该程序框图，若输出的的

   值为0，则输入的的值为

   A．      B．          C．           D．

6．在正方体中，为棱的中点，则异面直线与所成角

   的正切值为

   A． B． C．  D．

7．在直三棱柱中，，，则点到平面

   的距离为

   A． B． C．  D．

8. 已知圆：与圆：的公共弦所在直线

   恒过定点,且点在直线上,则的取值范围是

   A． B． C．  D．

9．已知，，，是同一球面上的四个点，其中是正三角形，平面

   ，，则该球的表面积为

   A． B． C．  D．

10.若动点分别在直线和上移动，

   则中点到原点距离的最小值为

   A． B． C．  D．

11.若方程 有两个相异的实根，则实数k的取值范围是

   A.     B.      C.      D.

12.已知点，点是圆上的动点，点是圆

   上的动点，则的最大值为

   A． B． C．  D．

二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)

13.若满足约束条件则的最大值为_______________.

14.若六进制数（为正整数）化为十进制为，则______________.

15.已知直线与圆心为的圆相交于两点，且

   为等边三角形，则实数______________.

16.学生到工厂劳动实践，利用3D打印技术制作模型.如图，该模型为长方体

   挖去四棱锥O­—EFGH后所得几何体，其中O为长方体的

   中心，E，F，G，H分别为所在棱的中点， 

   ，3D打印所

   用原料密度为0.9 g/cm3，不考虑打印损耗，

   制作该模型所需原料的质量为___________.

三、解答题(本大题共6小题，共70分，其中第

    1小题10分，其余各小题12分，解答时应

    写出必要的文字说明、证明过程或演算步骤）

17.（本小题满分10分）已知圆C经过点A(2，－1)，和直线x＋y＝1相切，且圆心在

    直线y＝－2x上.

   （1）求圆C的方程；

   （2）已知直线l经过（2,0）点，并且被圆C截得的弦长为2，求直线l的方程.

18．（本小题满分12分）已知四棱锥的底面ABCD是菱形，平面ABCD，

    ，，F，G分别为PD，BC中点，.

   （Ⅰ）求证：平面PAB；

   （Ⅱ）求三棱锥的体积；

19．（本小题满分12分）如图，在三棱锥中，顶点在底面上的投影

    在棱上，，，

    ，为的中点．

   （1）求证：平面；

   （2）求二面角的余弦值；

20.（本小题满分12分）已知点在圆上运动，且存在一定点

    ，点为线段的中点.

   （1）求点的轨迹的方程；

   （2）过且斜率为的直线与点的轨迹交于不同的两点，是否存在

        实数使得，并说明理由.

21.（本小题满分12分）如图，四边形为正方形，，分别为，的中点，

    以为折痕把折起，使点到达点的位置，且．

   （1）证明：平面平面；

   （2）求与平面所成角的正弦值．

22．（本小题满分12分）已知圆，直线是圆

    与圆的公共弦所在直线方程，且圆的圆心在直线上．

   （1）求圆的方程；

   （2）过点分别作直线，，交圆于，，，四点，且

       ，求四边形面积的最大值与最小值．

阆中中学2020年秋高2019级期中教学质量检测（仁智）

数学参考答案（理科）

一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)

13.   9       14.   2  15.          16.     

三、解答题(本大题共6小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤)

17.(1)设圆心的坐标为C (a，－2a)，

则＝. 化简，得a2－2a＋1＝0，解得a＝1.

所以C点坐标为(1，－2)，半径r＝|AC|＝＝.

故圆C的方程为(x－1)2＋(y＋2)2＝2.

(2)①当直线l的斜率不存在时，直线l的方程为x＝2，此时直线l被圆C截得的弦长为2，

满足条件.

②当直线l的斜率存在时，设直线l的方程为y＝k（x—2），即 kx-y-2k=0

由题意得，解得k＝，则直线l的方程为y＝（x-2）.

综上所述，直线l的方程为x＝2或3x-4y-6＝0.

18.（Ⅰ）如图，连接， ∵是中点，是中点，

∴，而平面，平面，

∴平面，

又∵是中点，是中点，

∴，而平面，平面，

∴平面，又

∴平面平面，即平面.

（Ⅱ）∵底面，∴，又四边形为菱形，

∴，又，∴平面，而为的中点，

∴.

19.（1）因为顶点在底面上的射影在棱上，

所以平面，因为平面，所以平面平面，

因为，所以，因为平面平面，

平面，所以平面，又平面，所以，

由，，得，所以，

因为且平面，平面，平面，

所以平面.

（2）连接，

因为为的中点，为的中点，，所以，

如图，以为坐标原点，分别以，，为轴，轴，轴的正方向，建立空间直角坐标系，，

，

设为平面的一个法向量，

则.取，得，

设平面的一个法向量，则，取，则.  设二面角的平面角为，

则，

所以二面角的余弦值为.

20.（1）由中点坐标公式，得  即：，.

∵点在圆上运动，∴，

即，整理，得.

∴点的轨迹的方程为.

（2）设，，直线的方程是，代入圆.

可得，由，得，

且，，∴

.

.

解得或1，不满足.∴不存在实数使得.

21.（1）由已知可得，BF⊥PF，BF⊥EF，所以BF⊥平面PEF.

又平面ABFD，所以平面PEF⊥平面ABFD.

（2）作PH⊥EF，垂足为H.由（1）得，PH⊥平面ABFD.

以H为坐标原点，的方向为y轴正方向，为单位长，建立如图所示的空间直角坐标系H−xyz.

由（1）可得，DE⊥PE.又DP=2，DE=1，所以PE=.又PF=1，EF=2，故PE⊥PF.

可得.

则 为平面ABFD的法向量.

设DP与平面ABFD所成角为，则.

所以DP与平面ABFD所成角的正弦值为.

22.（1）圆的圆心在直线上，设圆心，由题意得，，即，到的距离，所以的半径，所以圆的方程：；

（2）当过点的互相垂直的直线，为轴，垂直于轴时，，这时直线的方程为，代入到圆中，，

所以，四边形的面积；

当过点的互相垂直的直线，不垂直于轴时，

设直线为：，则直线为：，

所以圆心到直线的距离，圆心到直线的距离，，，

设，当或1时，正好是轴及垂直轴，

面积，

当时，最大且，或1时，最小，

四边形面积的最大值17，最小值．