初中数学沪教版 (五四制)七年级下册第十三章 相交线 平行线综合与测试课时训练

这是一份初中数学沪教版 (五四制)七年级下册第十三章 相交线 平行线综合与测试课时训练，共29页。试卷主要包含了如图所示，直线l1∥l2，点A等内容，欢迎下载使用。
七年级数学第二学期第十三章相交线 平行线定向练习
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、若直线a∥b，b∥c，则a∥c的依据是（ ）．
A．平行的性质 B．等量代换
C．平行于同一直线的两条直线平行． D．以上都不对
2、如果两个角的一边在同一直线上，另一边互相平行，则这两个角（ ）
A．相等 B．互补 C．互余 D．相等或互补
3、下列命题正确的是（　　）
（1）两条直线被第三条直线所截，同位角相等；
（2）在同一平面内，过一点有且只有一条直线与已知直线垂直；
（3）平移前后连接各组对应点的线段平行且相等；
（4）从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离；
（5）在同一平面内，三条直线的交点个数有三种情况．
A．0个 B．1个 C．2个 D．3个
4、如图所示，直线l1∥l2，点A、B在直线l2上，点C、D在直线l1上，若△ABC的面积为S1，△ABD的面积为S2，则（ ）

A．S1＞S2 B．S1＝S2 C．S1＜S2 D．不确定
5、如图，AB∥CD，AE∥CF，∠C＝131°，则∠A＝（ ）

A．39° B．41° C．49° D．51°
6、如果同一平面内有三条直线，那么它们交点个数是（ ）个．
A．3个 B．1或3个 C．1或2或3个 D．0或1或2或3个
7、如图所示，下列条件中，不能推出AB∥CE成立的条件是（ ）

A．∠A＝∠ACE B．∠B＝∠ACE C．∠B＝∠ECD D．∠B+∠BCE＝180°
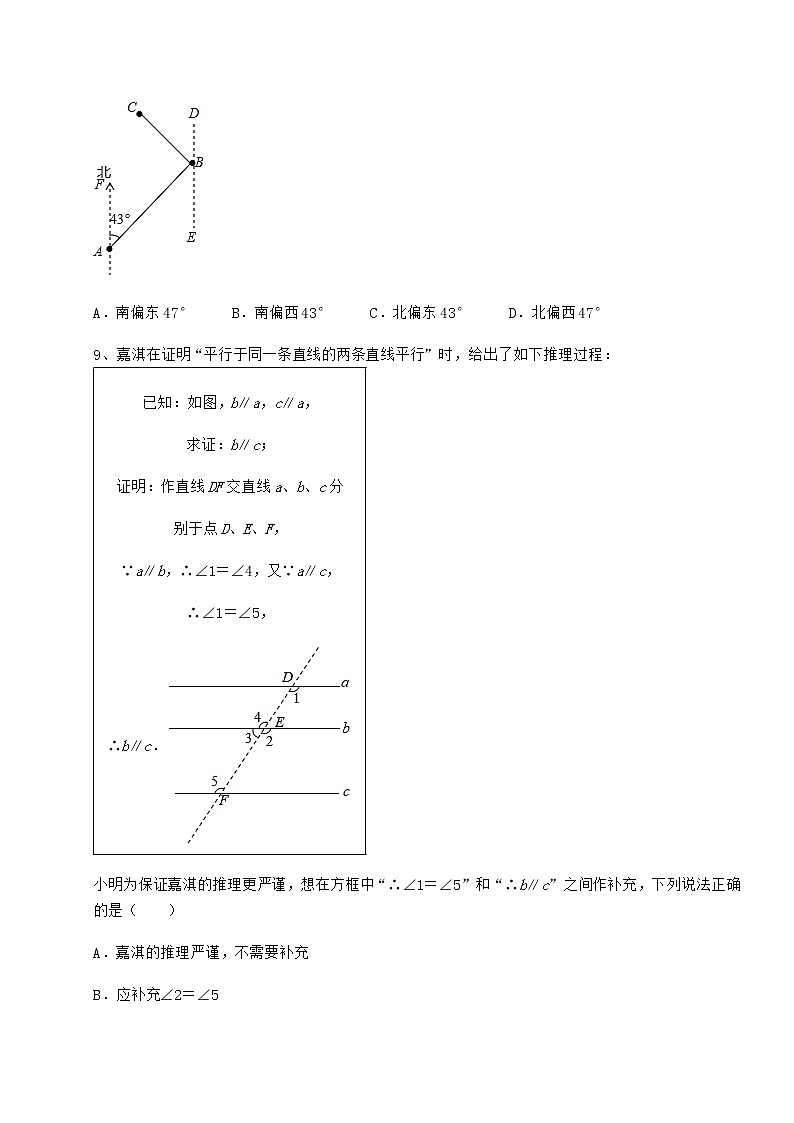
8、如图，有A，B，C三个地点，且∠ABC＝90°，B地在A地的北偏东43°方向，那么C地在B地的（　　）方向．

A．南偏东47° B．南偏西43° C．北偏东43° D．北偏西47°
9、嘉淇在证明“平行于同一条直线的两条直线平行”时，给出了如下推理过程：
已知：如图，b∥a，c∥a，
求证：b∥c；
证明：作直线DF交直线a、b、c分
别于点D、E、F，
∵a∥b，∴∠1＝∠4，又∵a∥c，
∴∠1＝∠5，
∴b∥c．
小明为保证嘉淇的推理更严谨，想在方框中“∴∠1＝∠5”和“∴b∥c”之间作补充，下列说法正确的是（　　）
A．嘉淇的推理严谨，不需要补充
B．应补充∠2＝∠5
C．应补充∠3+∠5＝180°
D．应补充∠4＝∠5
10、如图所示，下列说法错误的是（　　）

A．∠1和∠3是同位角 B．∠1和∠5是同位角
C．∠1和∠2是同旁内角 D．∠5和∠6是内错角
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，若，被所截，则与______________是内错角．

2、如图将一条两边互相平行的纸带按如图折叠，若∠EFG＋∠EGD=150°，则∠EGD=_____

3、已知：某小区地下停车场的栏杆如图所示，当栏杆抬起到最大高度时∠ABC=150°，若此时CD平行地面AE，则_________度．

4、如图在△ABC中，AB＝AC＝5，S△ABC＝10，AD是△ABC的中线，F是AD上的动点，E是AC边上的动点，则CF＋EF的最小值为______．

5、已知，线段AB垂直于线段CD，垂足为O，OE平分∠AOC，∠BOF＝28°，则∠EOF＝____°．
三、解答题（10小题，每小题5分，共计50分）
1、已知：如图，中，点、分别在、上，交于点， ，．

（1）求证：；
（2）若平分，，求的度数．
2、如图，直线AB、CD相交于点O，已知OE平分∠BOD，且∠AOC：∠AOD＝3：7．
（1）求∠DOE的度数；
（2）若∠EOF是直角，求∠COF的度数．

3、如图所示，点、分别在、上，、均与相交，，，求证：．

4、如果把图看成是直线AB，EF被直线CD所截，那么
（1）∠1与∠2是一对什么角？
（2）∠3与∠4呢？∠2与∠4呢？

5、如图，已知，，，试说明直线AD与BC垂直（请在下面的解答过程的空格内填空或在括号内填写理由）．

理由：C，（已知）
，（ ）
．（ ）
又，（已知）
=180°．（等量代换）
，（ ）
．（ ）
，（已知）
，
．
6、如图，直线AB与CD相交于点O，OC平分∠BOE，OF⊥CD，垂足为点O．
（1）写出∠AOF的一个余角和一个补角．
（2）若∠BOE＝60°，求∠AOD的度数．
（3）∠AOF与∠EOF相等吗？说明理由．

7、如图，平面上有三个点A、B、C．

（1）根据下列语句按要求画图．
①画射线AB，用圆规在线段AB的延长线上截取BD＝AB（保留作图痕迹）；
②连接CA、CD、CB；
③过点C画CE⊥AD，垂足为点E；
④过点D画DF∥AC，交CB的延长线于点F．
（2）①在线段CA、CE、CD中，线段_________最短，依据是_________．
②用刻度尺或圆规检验DF与AC的大小关系为_________．
8、如图，点O在直线AB上，过点O作射线OC，OP平分∠AOC，ON平分∠POB．∠AOC＝38°，求∠CON的度数．

9、如图，已知∠A＝120°，∠FEC＝120°，∠1＝∠2，试说明∠FDG＝∠EFD．请补全证明过程，即在下列括号内填上结论或理由．

解：∵∠A＝120°，∠FEC＝120°（已知），
∴∠A＝　 （　 　）．
∴AB∥　 （　 　）．
又∵∠1＝∠2（已知），
∴AB∥CD （　 　）．
∴EF∥　 　（　 　）．
∴∠FDG＝∠EFD （　 　）．
10、如图，107国道上有一个出口M，想在附近公路旁建一个加油站，欲使通道最短，应沿怎样的线路施工？


-参考答案-
一、单选题
1、C
【分析】
根据平行公理的推论进行判断即可．
【详解】
解：直线a∥b，b∥c，则a∥c的依据是平行于同一直线的两条直线平行，
故选：C．
【点睛】
本题考查了平行公理的推论，解题关键是明确平行于同一直线的两条直线平行．
2、D
【分析】
根据平行线的性质，结合图形解答即可．
【详解】
如图，当AE∥BD时，∠EAB与∠DBC符合题意，
∴∠EAB=∠DBC；

如图，当AE∥BD时，∠EAF与∠DBC符合题意，
∵∠EAB+∠EAF=180°，∠EAB=∠DBC，
∴∠DBC +∠EAF=180°，
故选D．
【点睛】
本题考查了平行线的性质，熟练掌握平行线的性质，灵活运用属性结合是解题的关键．
3、B
【分析】
根据平行线的性质、垂直的定义、平移的性质、点到直线的距离的定义、直线的位置关系逐个判断即可得．
【详解】
解：（1）两条平行线被第三条直线所截，同位角相等；则原命题错误；
（2）在同一平面内，过一点有且只有一条直线与已知直线垂直；则原命题正确；
（3）平移前后连接各组对应点的线段平行（或在同一条直线上）且相等；则原命题错误；
（4）从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离；则原命题错误；
（5）在同一平面内，三条直线的交点个数可能为0个或1个或2个或3个，共有四种情况；则原命题错误；
综上，命题正确的是1个，
故选：B．
【点睛】
本题考查了平行线的性质、垂直的定义、平移的性质、点到直线的距离的定义、直线的位置关系，熟练掌握各定义和性质是解题关键．
4、B
【分析】
由题意根据两平行线间的距离处处相等，可知△ABC和△ABD等底等高，结合三角形的面积公式从而进行分析即可．
【详解】
解：因为l1∥l2，所以C、D两点到l2的距离相等，即△ABC和△ABD的高相等．同时△ABC和△ABD有共同的底AB，所以它们的面积相等．
故选：B.
【点睛】
本题考查平行线间的距离以及三角形的面积，解题时注意等高等底的两个三角形的面积相等．
5、C
【分析】
由题意直接根据平行线的性质进行分析计算即可得出答案．
【详解】
解：如图，

∵AB∥CD，∠C＝131°，
∴∠1 =180°-∠C=49°（两直线平行，同旁内角互补），
∵AE∥CF，
∴∠A=∠C=49°（两直线平行，同位角相等）．
故选：C．
【点睛】
本题主要考查平行线的性质，熟练掌握平行线的性质即两直线平行，同旁内角互补和两直线平行，同位角相等以及两直线平行，内错角相等是解答此题的关键．
6、D
【分析】
根据三条直线是否有平行线分类讨论即可．
【详解】
解：当三条直线平行时，交点个数为0；
当三条直线相交于1点时，交点个数为1；
当三条直线中，有两条平行，另一条分别与他们相交时，交点个数为2；
当三条直线互相不平行时，且交点不重合时，交点个数为3；
所以，它们的交点个数有4种情形．
故选：D．
【点睛】
本题考查多条直线交点问题，解题关键是根据三条直线中是否有平行线和是否交于一点进行分类讨论．
7、B
【分析】
根据平行线的判定定理分析即可．
【详解】
A、∠A和∠ACE是AB与CE被AC所截形成的内错角，则∠A＝∠ACE时，可以推出AB∥CE，不符合题意；
B、∠B和∠ACE不属于AB与CE被第三条直线所截形成的任何角，则∠B＝∠ACE时，无法推出AB∥CE，符合题意；
C、∠B和∠ECD是AB与CE被BD所截形成的同位角，则∠B＝∠ECD时，可以推出AB∥CE，不符合题意；
D、∠B和∠BCE AB与CE被BD所截形成的同旁内角，则∠B+∠BCE＝180°时，可以推出AB∥CE，不符合题意；
故选：B．
【点睛】
本题考查平行线的判定，理解并熟练运用平行线的判定定理是解题关键．
8、D
【分析】
根据方向角的概念，和平行线的性质求解．
【详解】
解：如图：

∵AF∥DE，
∴∠ABE＝∠FAB＝43°，
∵AB⊥BC，
∴∠ABC＝90°，
∴∠CBD＝180°﹣90°﹣43°＝47°，
∴C地在B地的北偏西47°的方向上．
故选：D．
【点睛】
本题主要考查了方位角，平行线的性质，正确的识别图形是解题的关键．
9、D
【分析】
根据平行线的性质与判定、平行公理及推论解决此题．
【详解】
解：证明：作直线DF交直线a、b、c分别于点D、E、F，
∵a∥b，
∴∠1=∠4，
又∵a∥c，
∴∠1=∠5，
∴∠4=∠5．
∴b∥c．
∴应补充∠4=∠5．
故选：D．
【点睛】
本题主要考查平行线的性质与判定、平行公理及推论，熟练掌握平行线的性质与判定、平行公理及推论是解决本题的关键．
10、B
【分析】
根据同位角、内错角、同旁内角的意义：两条直线被第三条直线所截，在截线的同旁，在被截的两直线的同一侧的角叫做同位角；两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间的两个角叫做内错角；两条直线被第三条直线所截，在截线同旁，且在被截两条直线之内的两角叫做同旁内角，可得答案．
【详解】
解：A、∠1和∠3是同位角，故此选项不符合题意；
B、∠1和∠5不存在直接联系，故此选项符合题意；
C、∠1和∠2是同旁内角，故此选项不符合题意；
D、∠1和∠6是内错角，故此选项不符合题意；
故选B．
【点睛】
本题考查了同位角、内错角、用旁内角，利用同位角、内错角、同旁内角的意义是解题关键．
二、填空题
1、
【分析】
根据内错角的定义填空即可．
【详解】
解：与是内错角，
故答案为
【点睛】
本题主要考查内错角的定义，解答此类题确定三线八角是关键，可直接从截线入手．同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形．
2、
【分析】
先根据平行线的性质得到，结合已知∠EFG＋∠EGD=150°，解得∠EGD=，再根据折叠的性质解得，结合两直线平行，同旁内角互补得到，据此整理得，进而解题．
【详解】
解：

∠EFG＋∠EGD=150°，
∠EGD=
折叠







故答案为：．
【点睛】
本题考查折叠的性质、平行线的性质等知识，两直线平行，同旁内角互补，掌握相关知识是解题关键．
3、120
【分析】
过点B作BF∥CD，因为AB⊥AE，可得∠ABF=90°，即可得出∠FBC的度数，再由BF∥CD，可得∠FBC+∠BCD=180°，代入计算即可得出答案．
【详解】
解：过点B作BF∥CD，如图，

由题意可知，∠ABF=90°，
∵∠ABC=150°，
∴∠FBC=∠ABC-∠ABF=150°-90°=60°，
∵BF∥CD，
∴∠FBC+∠BCD=180°，
∴∠BCD=180°-∠FBC=180°-60°=120°．
故答案为：120．
【点睛】
本题主要考查了平行线的性质，熟练应用平行线的性质进行求解是解决本题的关键．
4、4
【分析】
作E关于AD的对称点M，连接CM交AD于F，连接EF，过C作CN⊥AB于N，根据三角形面积公式求出CN，根据对称性质求出CF＋EF＝CM，根据垂线段最短得出CF＋EF即可得出答案．
【详解】
解：方法一：作E关于AD的对称点M，连接CM交AD于F，连接EF，过C作CN⊥AB于N，
∵S△ABC＝×AB×CN，
∴CN＝4，
∵E关于AD的对称点M，
∴EF＝FM，
∴CF＋EF＝CF＋FM＝CM，
根据垂线段最短得出：CM≥CN，
即CF＋EF≥4，
即CF＋EF的最小值是4．

方法二：∵AB＝AC，AD是△ABC的中线，
∴AD⊥BC，
∴点C与点B关于AD对称，
过B作BE⊥AC于E，交AD于F，连接CF，
则此时，CF＋EF的值最小，且最小值为BE，
∵S△ABC＝•AC•BE＝10，
∴BE＝4，
∴CF＋EF的最小值4，

故答案为：4．
【点睛】
本题考查了垂线段最短以及对称轴作图，结合等腰三角形的性质取E或C对称点连接是解题的关键．
5、107
【分析】
分两种情况：①射线OF在∠BOC内部；②射线OF在∠BOD内部．
【详解】
解：∵AB⊥CD，垂足为O，
∴∠AOC=∠COB=90°，
∵OE平分∠AOC，
∴∠AOE=∠COE=∠AOC=45°．
分两种情况：
①如图1，射线OF在∠BOC内部时，

∵∠AOE=45°，∠BOF=28°，
∴∠EOF=180°-∠AOE-∠BOF=107°；
②如图2，射线OF在∠BOD内部时，

∵∠COE=45°，∠COB=90°，∠BOF=28°，
∴∠EOF=∠COE+∠COB+∠BOF=163°．
故答案为107或163．
【点睛】
本题考查了垂直的定义，角平分线定义以及角的计算，进行分类讨论是解题的关键．
三、解答题
1、（1）见解析；（2）72°
【分析】
（1）等量代换得出∠3＝∠DFE，平行线的判定得出EF//AB，可以推出∠ADE＝∠B，即可判断结论；
（2）由平分线的定义得出∠ADE＝∠EDC＝∠B，由平角的定义列出关于∠5+∠ADE+∠EDC＝＝180°，求出∠B的度数，即可得出∠ADC的度数，由EF//AB即可求出∠2的度数．
【详解】
解：（1）∵，∠2+∠DFE＝180°，
∴∠3＝∠DFE，
∴EF//AB，
∴∠ADE＝∠1，
又∵，
∴∠ADE＝∠B，
∴DE//BC，
（2）∵平分，
∴∠ADE＝∠EDC，
∵DE//BC，
∴∠ADE＝∠B，
∵
∴∠5+∠ADE+∠EDC＝＝180°，
解得：，
∴∠ADC＝2∠B＝72°，
∵EF//AB，
∴∠2＝∠ADC＝180°－108°＝72°，
【点睛】
本题考查了平行线的判定和性质、邻补角、角平分线的定义等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
2、（1）；（2）
【分析】
（1）由∠AOC：∠AOD＝3：7，先求解 再利用对顶角相等求解 结合角平分线的定义可得答案；
（2）先求解 再利用平角的定义可得答案.
【详解】
解：（1） ∠AOC：∠AOD＝3：7，


OE平分∠BOD，

（2）


【点睛】
本题考查的是角平分线的定义，对顶角的性质，平角的定义，垂直的定义，角的和差运算，掌握“几何图形中角的和差关系”是解本题的关键.
3、证明见解析
【分析】
由，证明，再证，最后根据对顶角相等，可得答案．
【详解】
证明：∵，
∴，
∴∠ABD=∠D，
又∵，
∴∠ABD=∠C，
∴，
∴，
∵，
∴．
【点睛】
本题主要考查了平行线的性质与判定，对顶角的性质，解题的关键在于能够熟练掌握相关知识进行求解．
4、（1）∠1与∠2是一对同位角；（2）∠3与∠4是一对内错角，∠2与∠4是一对同旁内角
【分析】
同位角：两条直线被第三条直线所截，在截线的同旁，被截两直线的同一侧的角，我们把这样的两个角称为同位角；内错角：两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角；同旁内角：两条直线被第三条直线所截，在截线同旁，且在被截直线之间的两角，叫做同旁内角；由以上概念进行判断即可．
【详解】
解：直线AB，EF被直线CD所截，
（1）∠1与∠2是一对同位角；
（2）∠3与∠4是一对内错角，∠2与∠4是一对同旁内角．
【点睛】
本题考查同位角、内错角以及同旁内角的识别，掌握这几种角的基本定义是解题关键．
5、GD；AC；同位角相等，两直线平行；；两直线平行，内错角相等；；AD；EF；同旁内角互补，两直线平行；两直线平行，同位角相等；AD；BC
【分析】
结合图形，根据平行线的判定和性质逐一进行填空即可．
【详解】
解：，已知
，同位角相等，两直线平行
两直线平行，内错角相等

又，（已知）
（等量代换）
，同旁内角互补，两直线平行）
（两直线平行，同位角相等）
，（已知）
，
，
．
【点睛】
本题主要考查了平行线的判定和性质，垂线的定义，解答此题的关键是注意平行线的性质和判定定理的综合运用．
6、（1）∠AOF的余角是：∠COE或∠BOC或∠AOD；∠AOF的补角是∠BOF；（2）30°；（3）∠AOF=∠EOF，理由见解析
【分析】
（1）由OC⊥CD，可得∠DOF=90°，则∠AOF+∠AOD=90°，由对顶角相等得∠BOC=∠AOD，则∠AOF+∠BOC=90°，由OC平分∠BOE，可得∠COE=∠BOC，∠AOF+∠COE=90°；由∠AOF+∠BOF=180°，可得∠AOF的补角是∠BOF；
（2）由OC平分∠BOE，∠BOE=60°，可得∠BOC=30°，再由∠AOD=∠BOC，即可得到∠AOD=30°；
（3）由（1）可得∠AOD=∠BOC=∠COE，再由OF⊥OC，得到∠DOF=∠COF=90°，则∠AOD+∠AOF=∠EOF+∠COE=90°，即可推出∠AOF=∠EOF．
【详解】
解：（1）∵OC⊥CD，
∴∠DOF=90°，
∴∠AOF+∠AOD=90°，
又∵∠BOC=∠AOD，
∴∠AOF+∠BOC=90°，
∵OC平分∠BOE，
∴∠COE=∠BOC，
∴∠AOF+∠COE=90°；
∴∠AOF的余角是，∠COE，∠BOC，∠AOD；
∵∠AOF+∠BOF=180°，
∴∠AOF的补角是∠BOF；
（2）∵OC平分∠BOE，∠BOE=60°，
∴∠BOC=30°，
又∵∠AOD=∠BOC，
∴∠AOD=30°；
（3）∠AOF=∠EOF，理由如下：
由（1）可得∠AOD=∠BOC=∠COE，
∵OF⊥OC，
∴∠DOF=∠COF=90°，
∴∠AOD+∠AOF=∠EOF+∠COE=90°，
∴∠AOF=∠EOF．
【点睛】
本题主要考查了与余角、补角有关的计算，等角的余角相等，垂线的定义，解题的关键在于熟知余角与补角的定义：如果两个角的相加的度数为90度，那么这两个角互余，如果两个角相加的度数为180度，那么这两个角互补．
7、（1）见解析；（2）①；垂线段最短；②相等
【分析】
（1）根据题意作图即可；
（2）根据垂线段最短以及圆规进行检验即可．
【详解】
（1）如图所示，即为所求；

（2）①根据垂线段最短可知，在线段CA、CE、CD中，线段CE最短；
②用圆规检验DF=AC．
【点睛】
本题主要考查了画平行线，画垂线，画线段，垂线段最短等等，熟知相关知识是解题的关键．
8、61.5°
【分析】
由题意易得∠AOP＝∠COP＝∠AOC＝19°，然后根据邻补角可得∠BOP＝161°，进而根据角的和差关系可求解．
【详解】
解：∵OP平分∠AOC，∠AOC＝38°，
∴∠AOP＝∠COP＝∠AOC＝×38°＝19°，
∴∠BOP＝180°﹣∠AOP＝180°﹣19°＝161°，
∵ON平分∠POB
∴∠PON＝∠BOP＝×161°＝80.5°，
∴∠CON＝∠PON﹣∠COP＝80.5°﹣19°＝61.5°．
【点睛】
本题主要考查角平分线的定义、邻补角及角的和差关系，熟练掌握角平分线的定义、邻补角及角的和差关系是解题的关键．
9、∠FEC；等量代换；EF；同位角相等，两直线平行；内错角相等，两直线平行；CD；平行于同一条直线的两直线互相平行；两直线平行，内错角相等
【分析】
利用平行线的判定，由已知得AB∥EF、AB∥CD，可推出EF∥CD，利用平行线的性质得结论
【详解】
解：∵∠A=120°，∠FEC=120°（已知），
∴∠A=∠FEC（等量代换），
∴AB∥EF（同位角相等，两直线平行），
又∵∠1=∠2（已知），
∴AB∥CD（内错角相等，两直线平行），
∴EF∥CD（平行于同一条直线的两直线互相平行），
∴∠FDG=∠EFD（两直线平行，内错角相等），
故答案为：∠FEC；等量代换；EF；同位角相等，两直线平行；内错角相等，两直线平行；CD；平行于同一条直线的两直线互相平行；两直线平行，内错角相等．
【点睛】
本题考查了平行线的性质和判定，学会分析，正确的利用平行线的性质和判定是解决本题的关键．
10、作图见解析
【分析】
根据垂线段最短作图即可；
【详解】
解：如图，过点M作MN⊥，垂足为N，欲使通道最短，应沿线路MN施工.

【点睛】
本题主要考查了垂线段最短的应用，尺规作图，准确分析作图是解题的关键．