2021学年第十三章 相交线 平行线综合与测试同步测试题

这是一份2021学年第十三章 相交线 平行线综合与测试同步测试题，共28页。试卷主要包含了下列说法等内容，欢迎下载使用。
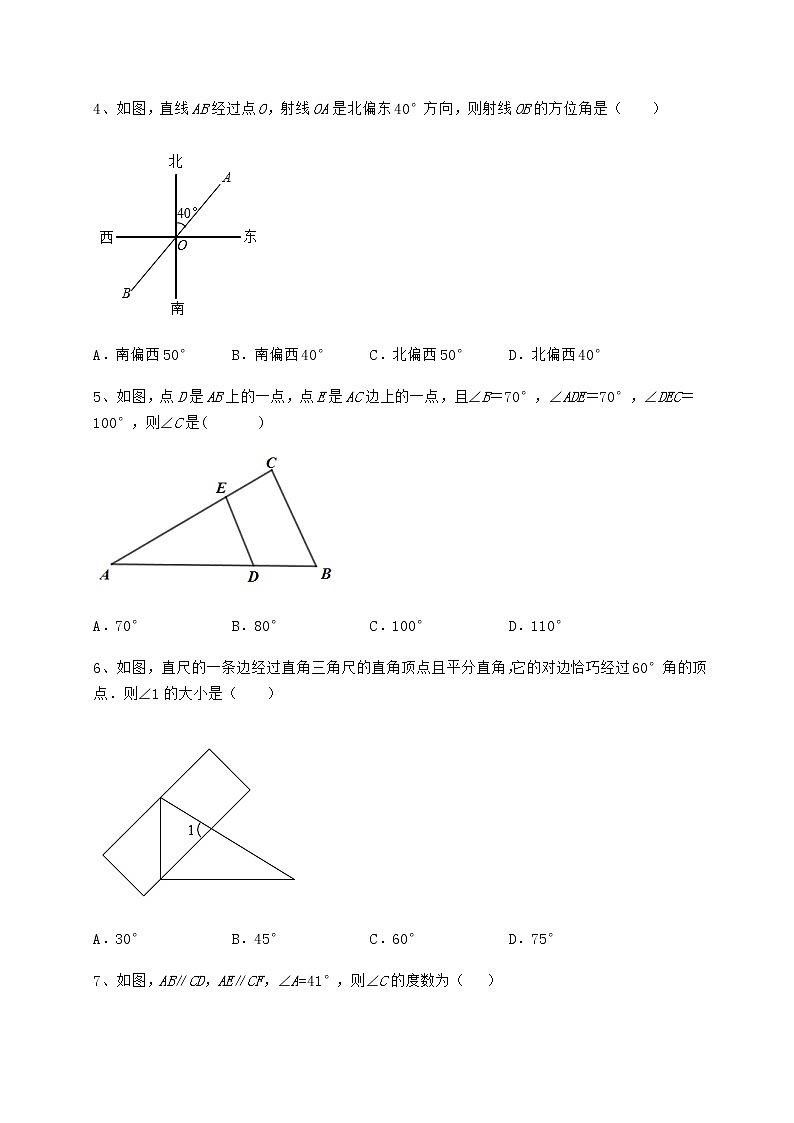
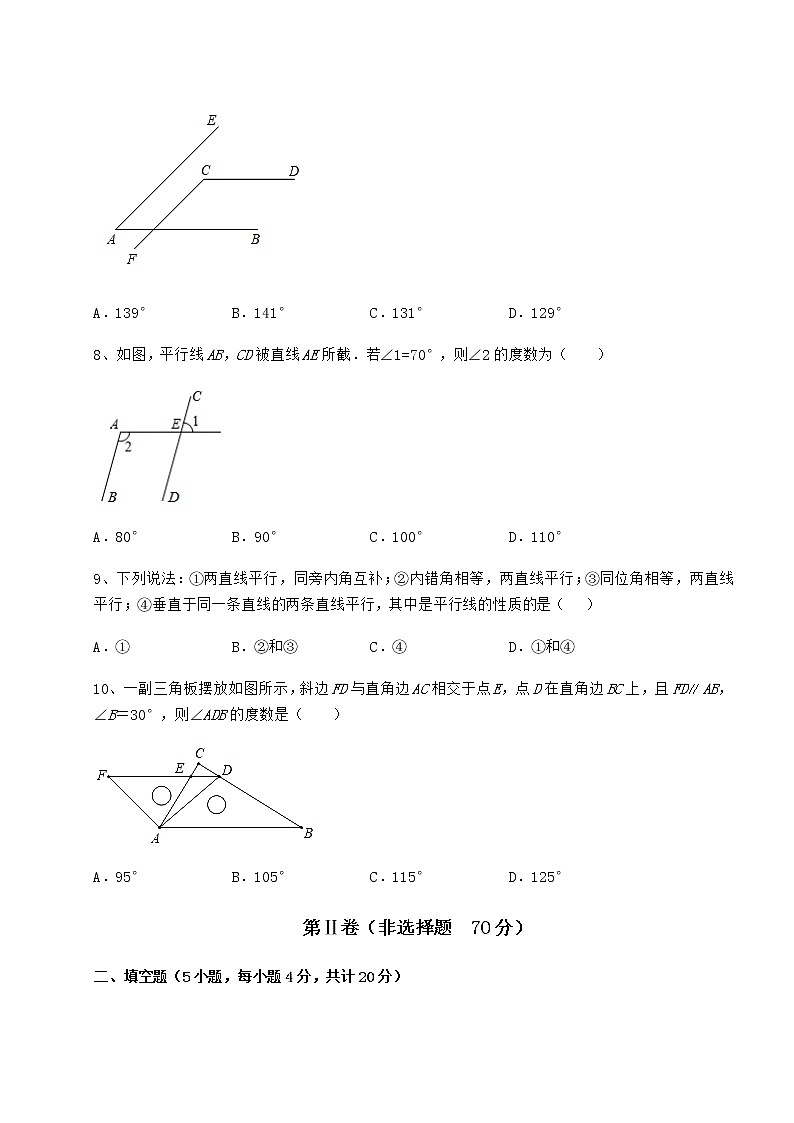
七年级数学第二学期第十三章相交线 平行线定向测试 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，O为直线AB上一点，∠COB＝36°12'，则∠AOC的度数为（　　）A．164°12' B．136°12' C．143°88' D．143°48'2、如图，不能推出a∥b的条件是（　　）A．∠4＝∠2 B．∠3+∠4＝180° C．∠1＝∠3 D．∠2+∠3＝180°3、∠A两边分别垂直于∠B的两边，∠A与∠B的关系是（   ）A．相等 B．互补 C．相等或互补 D．不能确定4、如图，直线AB经过点O，射线OA是北偏东40°方向，则射线OB的方位角是（    ）A．南偏西50° B．南偏西40° C．北偏西50° D．北偏西40°5、如图，点D是AB上的一点，点E是AC边上的一点，且∠B＝70°，∠ADE＝70°，∠DEC＝100°，则∠C是(       )A．70° B．80° C．100° D．110°6、如图，直尺的一条边经过直角三角尺的直角顶点且平分直角，它的对边恰巧经过60°角的顶点．则∠1的大小是（　　）A．30° B．45° C．60° D．75°7、如图，AB∥CD，AE∥CF，∠A=41°，则∠C的度数为（   ）A．139° B．141° C．131° D．129°8、如图，平行线AB，CD被直线AE所截．若∠1=70°，则∠2的度数为（    ）A．80° B．90° C．100° D．110°9、下列说法：①两直线平行，同旁内角互补；②内错角相等，两直线平行；③同位角相等，两直线平行；④垂直于同一条直线的两条直线平行，其中是平行线的性质的是（   ）A．① B．②和③ C．④ D．①和④10、一副三角板摆放如图所示，斜边FD与直角边AC相交于点E，点D在直角边BC上，且FDAB，∠B＝30°，则∠ADB的度数是（　　）A．95° B．105° C．115° D．125°第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，若，被所截，则与______________是内错角．2、规律探究：同一平面内有直线a1，a2，a3…，a100，若a1⊥a2，a2∥a3，a3⊥a4…，按此规律，a1和a100的位置是________．3、如图，点E是BA延长线上一点，下列条件中：①∠1＝∠3；②∠5＝∠D；③∠2＝∠4；④∠B+∠BCD＝180°，能判定ABCD的有___．（填序号）4、如图，直线AB和直线CD相交于点O，且∠AOC＝2∠BOC，则∠AOD的度数为____________．5、在体育课上某同学跳远的情况如图所示，直线表示起跳线，经测量，PB＝3.3米，PC=3.1米，PD=3.5米，则该同学的实际立定跳远成绩是___________米；三、解答题（10小题，每小题5分，共计50分）1、如图，107国道上有一个出口M，想在附近公路旁建一个加油站，欲使通道最短，应沿怎样的线路施工？2、如图，长方形纸片ABCD，点E，F，C分别在边AD，AB，CD上．将∠AEF沿折痕EF翻折，点A落在点A'处；将∠DEG沿折痕EG翻折，点D落在点D'处．（1）如图1，若∠AEF＝40°，∠DEG＝35°，求∠A'ED'的度数；（2）如图1，若∠A'ED'＝α，求∠FEG的度数（用含α的式子表示）；（3）如图2，若∠A'ED'＝α，求∠FEG的度数（用含α的式子表示）．3、如图，平面上有三个点A、B、C．（1）根据下列语句按要求画图．①画射线AB，用圆规在线段AB的延长线上截取BD＝AB（保留作图痕迹）；②连接CA、CD、CB；③过点C画CE⊥AD，垂足为点E；④过点D画DF∥AC，交CB的延长线于点F．（2）①在线段CA、CE、CD中，线段_________最短，依据是_________．②用刻度尺或圆规检验DF与AC的大小关系为_________．4、如图，已知BC，DE相交于点O，给出以下三个判断：①ABDE；②BCEF；③∠B=∠E．请你以其中两个判断作为条件，另外一个判断作为结论，写出所有的命题，指出这些命题是真命题还是假命题，并选择其中的一个真命题加以证明．5、如图，AE＝AF，以AE为直径作⊙O交EF点D，过点D作BC⊥AF，交AE的延长线于点B．（1）判断直线BC与⊙O的位置关系，并说明理由；（2）若AE＝5，AC＝4，求BE的长．6、如图，，P为，之间的一点，已知，，求∠1的度数．7、如图，OB⊥OD，OC平分∠AOD，∠BOC＝35°，求∠AOD和∠AOB的大小．8、如图所示，点、分别在、上，、均与相交，，，求证：．9、阅读并完成下列推理过程，在括号内填写理由．已知：如图，点，分别在线段、上，，平分，平分交于点、．求证：．证明：平分（已知），　　．平分（已知），　　（角平分线的定义），（已知），　　．　　．　　．10、如图，AB与EF交于点B，CD与EF交于点D，根据图形，请补全下面这道题的解答过程．（1）∵∠1=∠2（已知）∴           CD（                 ）∴∠ABD+∠CDB =           （                 ）（2）∵∠BAC =65°，∠ACD=115°，( 已知  ) ∴∠BAC+∠ACD=180° (等式性质)∴ABCD （                 ）（3）∵CD⊥AB于D，EF⊥AB于F，∠BAC=55°（已知）∴∠ABD=∠CDF=90°（ 垂直的定义）∴                      （同位角相等，两直线平行）又∵∠BAC=55°，（已知）∴∠ACD =           （                 ） -参考答案-一、单选题1、D【分析】根据邻补角及角度的运算可直接进行求解．【详解】解：由图可知：∠AOC+∠BOC=180°，∵∠COB＝36°12'，∴∠AOC=180°-∠BOC=143°48'，故选D．【点睛】本题主要考查邻补角及角度的运算，熟练掌握邻补角及角度的运算是解题的关键．2、B【分析】根据平行线的判定方法，逐项判断即可．【详解】解：、和是一对内错角，当时，可判断，故不符合题意；、和是邻补角，当时，不能判定，故符合题意；、和是一对同位角，当时，可判断，故不合题意；、和是一对同旁内角，当时，可判断，故不合题意；故选B．【点睛】本题考查了平行线的判定．解题的关键是：正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键．3、C【分析】分别画出∠A两边分别垂直于∠B的两边，然后利用同角的余角相等进行求解即可．【详解】解：如图所示：BE⊥AE，BC⊥AC，∴∠BCF=∠AEF=90°，∴∠A+∠AFE=90°，∠B+∠BFC=90°，∴∠A=∠B如图所示：BD⊥AD，BC⊥AC，∴∠ADE=∠BCE=90°，∴∠A+∠BEC=90°，∠CBE+∠BEC=90°，∴∠A=∠CBE，∵∠CBE+∠DBC=180°，∴∠A+∠DBC=180°，综上所述，∠A与∠B的关系是相等或互补，故选C．【点睛】本题主要考查了垂直的定义，同角的余角相等，以及等角的补角之间的关系，解题的关键在于能够根据题意画出图形进行求解．4、B【分析】由对顶角可知∠1=40°，故可知射线OB的方位角；【详解】解：由对顶角可知，∠1=40°所以射线OB的方位角是南偏西40°故答案为B【点睛】本题考查了方向角．解题的关键是掌握方向角的定义，方向角的表示方法是北偏东或北偏西，南偏东或南偏西．5、B【分析】先证明DEBC，根据平行线的性质求解．【详解】解：因为∠B＝∠ADE＝70°所以DEBC，所以∠DEC+∠C＝180°，所以∠C＝80°.故选：B．【点睛】此题主要考查平行线的判定与性质，解题的关键是熟知同位角相等，两直线平行．6、D【分析】由AC平分∠BAD，∠BAD=90°，得到∠BAC=45°，再由BD∥AC，得到∠ABD=∠BAC=45°，∠1+∠CBD=180°，由此求解即可．【详解】解：∵AC平分∠BAD，∠BAD=90°，∴∠BAC=45°∵BD∥AC，∴∠ABD=∠BAC=45°，∠1+∠CBD=180°，∵∠CBD=∠ABD+∠ABC=45°+60°=105°，∴∠1=75°，故选D．【点睛】本题主要考查了平行线的性质和角平分线的定义，解题的关键在于能够熟练掌握平行线的性质．7、A【分析】如图，根据AECF，得到∠CGB=41°，根据ABCD，即可得到∠C=139°．．【详解】解：如图，∵AECF，∴∠A=∠CGB=41°，∵ABCD，∴∠C=180°-∠CGB=139°．故选：A【点睛】本题考查了平行线的性质，熟知平行线的性质是解题关键．8、D【分析】直接利用对顶角以及平行线的性质分析得出答案．【详解】解：∵∠1＝70°，∴∠1＝∠3＝70°，∵ABDC，∴∠2＋∠3＝180°，∴∠2＝180°−70°＝110°．故答案为：D．【点睛】此题主要考查了平行线的性质以及对顶角，正确掌握平行线的性质是解题关键．9、A【分析】利用平行线的性质逐一判断即可．【详解】①是平行线的性质，故符合题意；②是平行线的判定，故不符合题意；③是平行线的判定，故不符合题意；④是平行线的判定，故不符合题意；故选：A．【点睛】本题主要考查平行线的性质，掌握平行线的性质和判定的区别是关键．10、B【分析】由题意可知∠ADF＝45°，则由平行线的性质可得∠B+∠BDF＝180°，求得∠BDF＝150°，从而可求∠ADB的度数．【详解】解：由题意得∠ADF＝45°，∵，∠B＝30°，∴∠B+∠BDF＝180°，∴∠BDF＝180°﹣∠B＝150°，∴∠ADB＝∠BDF﹣∠ADF＝105°．故选：B【点睛】本题主要考查平行线的性质，解答的关键是熟记平行线的性质：两直线平行，同旁内角互补．二、填空题1、【分析】根据内错角的定义填空即可．【详解】解：与是内错角，故答案为【点睛】本题主要考查内错角的定义，解答此类题确定三线八角是关键，可直接从截线入手．同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形．2、a1∥a100；【分析】从已知两直线的位置关系，运用平行线的性质，观察分析得几条特殊直线与a1的位置关系为a1∥a4，a1∥a5；a1⊥a2，a1 ⊥a3；且a1与an的位置关系是4为周期进行循环，下角标的余数为0或1时与a1平行，下角标的余数为2或3时与a1垂直，计算100=4×25，余数为0判定两直线的位置关系为a1∥a100．【详解】解：在同一平面内有直线两直线的位置，关系是相交或平行，如图所示：∵a1⊥a2，a2∥a3，∴a1 ⊥a3，又∵a3⊥a4，∴a1∥a4，又∵a4∥as，∴a1∥a5，又∵a5⊥a6，∴a1⊥a6，又∵a6∥a7，∴a1⊥a7，…从以上的规律可知：a1与an的位置关系是4为周期进行循环，若下角标的余数为0或1时与a1平行；若下角标的余数为2或3时与a1垂直．∵100=4×25，∴a1∥a100，故答案为：a1∥a100．【点睛】本题综合考查了平行线的性质，同一平面内图形的变化规律，倍数和余数的运用等相关知识点，重点是掌握平行线的性质，难点是掌握由特殊到一般图形变化规律在几何中的运用．3、②③④【分析】根据平行线的判定方法分别判定得出答案．【详解】解：①中，∵∠1＝∠3，∴AD//BC（内错角相等，两直线平行），故此选项不符合题意；②中，∵∠5＝∠D，∴AB//CD（内错角角相等，两直线平行），故此选项符合题意；③中，∵∠2＝∠4，∴AB//CD（内错角角相等，两直线平行）），故此选项符合题意；④中，∠B＋∠BCD＝180°，∴AB//CD （同旁内角互补，两直线平行），故此选项符合题意；故答案为：②③④．【点睛】此题主要考查了平行线的判定，正确掌握平行线的判定方法是解题关键．4、【分析】根据，可得，再根据对顶角相等即可求出的度数．【详解】解：∵，∴∴∵∴故答案为：【点睛】本题主要考查了邻补角、对顶角的相关知识，熟练运用邻补角、对顶角的相关知识是解答此题的关键．5、3.1【分析】根据点到直线，垂线段最短，即可求解．【详解】解：根据题意得：该同学的实际立定跳远成绩是PC=3.1米．故答案为：3.1【点睛】本题主要考查了点与直线的位置关系，熟练掌握点到直线，垂线段最短是解题的关键．三、解答题1、作图见解析【分析】根据垂线段最短作图即可；【详解】解：如图，过点M作MN⊥，垂足为N，欲使通道最短，应沿线路MN施工.【点睛】本题主要考查了垂线段最短的应用，尺规作图，准确分析作图是解题的关键．2、（1）；（2）；（3）【分析】（1）由折叠的性质，得到，，然后由邻补角的定义，即可求出答案；（2）由折叠的性质，先求出，然后求出∠FEG的度数即可；（3）由折叠的性质，先求出，然后求出∠FEG的度数即可．【详解】解：（1）将∠AEF沿折痕EF翻折，点A落在点A'处；将∠DEG沿折痕EG翻折，点D落在点D'处，∴，，∴；（2）根据题意，则，，∵，∴，∴，∴；（3）根据题意，，，∵，∴，∴，∴；【点睛】本题考查了折叠的性质，邻补角的定义，解题的关键是熟练掌握折叠的性质，正确得到，．3、（1）见解析；（2）①；垂线段最短；②相等【分析】（1）根据题意作图即可；（2）根据垂线段最短以及圆规进行检验即可．【详解】（1）如图所示，即为所求；（2）①根据垂线段最短可知，在线段CA、CE、CD中，线段CE最短；②用圆规检验DF=AC．【点睛】本题主要考查了画平行线，画垂线，画线段，垂线段最短等等，熟知相关知识是解题的关键．4、ABDE，BCEF，则∠B=∠E，此命题为真命题，见解析．【分析】三个判断任意两个为条件，另一个为结论可写三个命题，然后根据平行线的判定与性质判断这些命题的真假．【详解】（1）若AB∥DE，BC∥EF，则∠B=∠E，此命题为真命题．（2）若AB∥DE，∠B=∠E，则BC∥EF，此命题为真命题．（3）若∠B=∠E，BC∥EF，则AB∥DE，此命题为真命题．以第一个命题为例证明如下：∵AB∥DE，∴∠B=∠DOC.∵BC∥EF，∴∠DOC=∠E，∴∠B=∠E．【点睛】本题主要是考查了平行线的判定和性质，熟练掌握平行线的判定和性质求解该类题目的关键．5、（1）BC与⊙O相切，见解析；（2）．【分析】（1）连接OD，根据等腰三角形的性质得到∠OED＝∠ODE，∠OED＝∠F，求得∠ODE＝∠F，根据平行线的判定得到OD∥AC，根据平行线的性质得到∠ODB＝∠ACB，推出OD⊥BC，根据切线的判定定理即可得到结论；（2）根据平行线分线段成比例定理得到，于是得到结论．【详解】解：（1）BC与⊙O相切，理由：连接OD，∵OE＝OD，∴∠OED＝∠ODE，∵AE＝AF，∴∠OED＝∠F，∴∠ODE＝∠F，∴OD∥AC，∴∠ODB＝∠ACB，∵DC⊥AF，∴∠ACB＝90°，∴∠ODB＝90°，∴OD⊥BC，∵OD是⊙O的半径，∴BC与⊙O相切；（2）∵OD∥AC，∴，∵AE＝5，AC＝4，即，∴BE＝．【点睛】本题考查等腰三角形的性质、切线的判定与性质、平行线的判定与性质等知识，是重要考点，掌握相关知识是解题关键．6、30°【分析】首先过点P作射线，根据两直线平行，内错角相等，即可求得答案．【详解】过点P作射线，如图①．∵，，∴．∴．∵，∴．又∵．∴． 【点睛】此题考查了平行线的判定与性质．平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．7、∠AOD=110°，∠AOB=20°【分析】根据OB⊥OD，先可求出∠COD，再根据角平分线的性质求出∠AOD，利用角度的关系即可求出∠AOB．【详解】解：∵OB⊥OD∴∠BOD=90°∵∠BOC＝35°，∴∠COD=90°-∠BOC＝55°∵OC平分∠AOD，∴∠AOD=2∠COD=110°∴∠AOB=∠AOD-∠BOD=110°-90°=20°．【点睛】此题主要考查角度的求解，解题的关键是熟知角平分线的性质、垂直的定义．8、证明见解析【分析】由，证明，再证，最后根据对顶角相等，可得答案．【详解】证明：∵，∴，∴，又∵，∴，∴，∴，∵，∴．【点睛】本题主要考查了平行线的性质与判定，对顶角的性质，解题的关键在于能够熟练掌握相关知识进行求解．9、角平分线的定义；；两直线平行，同位角相等；等量代换；同位角相等，两直线平行．【分析】根据角平分线的定义和平行线的性质与判定即可证明．【详解】证明：平分（已知），（角平分线的定义）．平分（已知），（角平分线的定义），（已知），（两直线平行，同位角相等）．（等量代换）．（同位角相等，两直线平行）．故答案为：角平分线的定义；；两直线平行，同位角相等；等量代换；同位角相等，两直线平行．【点睛】本题主要考查了角平分线的定义，平行线的性质与判定，解题的关键在于能够熟练掌握相关知识进行求解．10、（1）AB；内错角相等，两直线平行；180°；两直线平行，同旁内角互补；（2）同旁内角互补，两直线平行；（3）AB；CD；125°；两直线平行，同旁内角互补.【分析】（1）由题意直接依据内错角相等，两直线平行进行分析以及两直线平行，同旁内角互补即可；（2）由题意直接依据同旁内角互补，两直线平行进行分析即可；（3）由题意直接根据两直线平行，同旁内角互补进行分析即可得出结论.【详解】解：（1）∵∠1=∠2 （已知）∴AB∥CD（内错角相等，两直线平行）∴∠ABD+ ∠BDC =180°（两直线平行，同旁内角互补）故答案为：AB；内错角相等，两直线平行；180°；两直线平行，同旁内角互补；（2）∵∠BAC =65°，∠ACD=115°，(已知) ∴∠BAC+∠ACD=180° (等式性质 )∴AB∥CD (同旁内角互补，两直线平行)故答案为：同旁内角互补，两直线平行；（3）∵CD⊥AB于D，EF⊥AB于F ，∠BAC=55°，（已知）∴∠ABD=∠CDF=90°（垂直的定义）∴AB ∥CD（同位角相等，两直线平行）又∵∠BAC=55°，（已知）∴∠ACD = 125°．（两直线平行，同旁内角互补）故答案为：AB；CD；125°；两直线平行，同旁内角互补.【点睛】本题考查平行线的判定与性质，熟练掌握平行线的判定与性质是解题的关键.