苏科版初中数学七年级下册——期中检测卷【含答案】

这是一份苏科版初中数学七年级下册——期中检测卷【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
期中检测卷
一、选择题（本大题共有10小题，每小题3分，共30分，以下各题都有四个选项，其中只有一个是正确的，选出正确答案，并在答题卡上将该项涂黑．）
1．（3分）计算（﹣a）2•a3的结果是（　　）
A．a5 B．a6 C．﹣a5 D．﹣a6
2．（3分）下列各式能用平方差分解因式的是（　　）
A．x2+2x﹣1 B．﹣1+x2 C．x+xy+1 D．x2﹣2x+1
3．（3分）如图直线AB，CD被EF所截，图中标注的角中是同位角的是（　　）

A．∠1与∠3 B．∠2与∠6 C．∠3与∠8 D．∠4与∠7
4．（3分）如图△ABC中，∠1=∠2，∠ABC=70°，则∠BDC的度数是（　　）

A．110° B．115° C．120° D．130°
5．（3分）若am=3，an=2，则a2m+n等于（　　）
A．11 B．12 C．16 D．18
6．（3分）如图在Rt△ABC中，∠B=90°，∠ACB=60°，EF∥GH，若∠1=58°，则∠2的度数是（　　）

A．22° B．26° C．28° D．32°
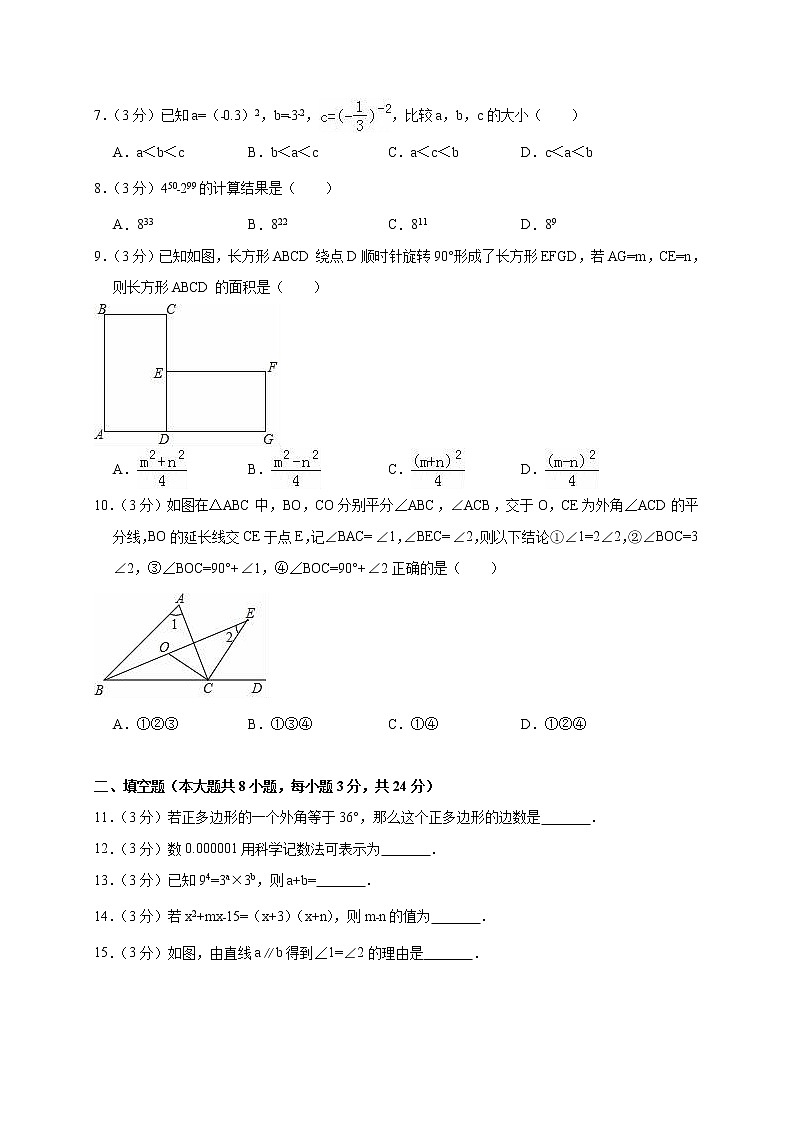
7．（3分）已知a=（﹣0.3）2，b=﹣3﹣2，，比较a，b，c的大小（　　）
A．a＜b＜c B．b＜a＜c C．a＜c＜b D．c＜a＜b
8．（3分）450﹣299的计算结果是（　　）
A．833 B．822 C．811 D．89
9．（3分）已知如图，长方形ABCD绕点D顺时针旋转90°形成了长方形EFGD，若AG=m，CE=n，则长方形ABCD的面积是（　　）

A． B． C． D．
10．（3分）如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，BO的延长线交CE于点E，记∠BAC=∠1，∠BEC=∠2，则以下结论①∠1=2∠2，②∠BOC=3∠2，③∠BOC=90°+∠1，④∠BOC=90°+∠2正确的是（　　）

A．①②③ B．①③④ C．①④ D．①②④
　
二、填空题（本大题共8小题，每小题3分，共24分）
11．（3分）若正多边形的一个外角等于36°，那么这个正多边形的边数是　 　．
12．（3分）数0.000001用科学记数法可表示为　 　．
13．（3分）已知94=3a×3b，则a+b=　 　．
14．（3分）若x2+mx﹣15=（x+3）（x+n），则m﹣n的值为　 　．
15．（3分）如图，由直线a∥b得到∠1=∠2的理由是　 　．

16．（3分）已知：s﹣t=3，则t2+6t﹣s2=　 　．
17．（3分）22﹣23﹣24﹣25……﹣22017+22018=　 　．
18．（3分）如图△ABC中，∠A=∠C，∠BDE=∠BED，BD平分∠ABC，若∠CDE=12°，则∠A=　 　．

　
三、解答题：（本大题共9小题，共76分.把解答过程写在答题卡相应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明）.
19．（16分）计算：
（1）（﹣2a2bc3）2
（2）（﹣a2）3•（﹣a3）2
（3）（2a﹣b）2﹣a（3a﹣2b）
（4）（2a+b﹣3）（2a﹣b﹣3）
20．（16分）将下列各式分解因式：
（1）2ax2﹣8a
（2）x2﹣6xy+5y2
（3）（2m﹣n）2﹣6n（2m﹣n）+9n2
（4）a2﹣b2+2b﹣1
21．（5分）先化简，再求值：（x﹣2）2+2（x﹣2）（x+4）﹣（x﹣3）（x+3），其中x=﹣2．
22．（5分）已知4m+3×8m+1÷24m+7=16，求m的值．
23．（6分）如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）．

（1）分别画出△ABC中BC边上的高AH、中线AG．
（2）画出先将△ABC向右平移6格，再向上平移3格后的△DEF．
（3）画一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积的2倍．
24．（6分）已知a+2b=1，ab=﹣1，求下列代数式的值：
（1）a2+4b2
（2）（a﹣2b）2
25．（6分）将一副直角三角尺BAC和ADE如图放置，其中∠BAC=∠ADE=90°，∠BCA=30°，
∠AED=45°，若∠AFD=75°，试判断AE与BC的位置关系，并说明理由．

26．（8分）阅读下列材料：
“a2≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式．例如：x2+4x+5=x2+4x+4+1=（x+2）2+1
∵（x+2）2≥0，
∴（x+2）2+1≥1，
∴x2+4x+5≥1．
试利用“配方法”解决下列问题：
（1）填空：x2﹣4x+5=（x　 　）2+1；
（2）已知x2+y2=4x﹣2y﹣5，求xy的值；
（3）比较代数式2x2﹣1与4x﹣5的大小．
27．（8分）在正方形ABCD中，∠C=∠D=90°，点E、F分别是边CD、BC上的中点，点P是一动点．记∠DEP=∠1，∠BFP=∠2，∠EPF=∠α．

（1）如图1，若点P运动到线段AD中点时，∠α=　 　，∠1+∠2=　 　．
（2）如图2，若点P在线段AD上运动时，∠1、∠2和∠α之间有何关系？
（3）当点P在直线AD上（在线段AD之外且PE与PF不重合）运动时，∠1、∠2和∠α之间又有何关系？说明理由．
　

参考答案
　
一、选择题（本大题共有10小题，每小题3分，共30分，以下各题都有四个选项，其中只有一个是正确的，选出正确答案，并在答题卡上将该项涂黑．）
1．（3分）计算（﹣a）2•a3的结果是（　　）
A．a5 B．a6 C．﹣a5 D．﹣a6
【分析】利用同底数幂的乘法运算，即可求得答案；注意同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加．
【解答】解：（﹣a）2•a3=a2•a3=a5．
故选：A．
2．（3分）下列各式能用平方差分解因式的是（　　）
A．x2+2x﹣1 B．﹣1+x2 C．x+xy+1 D．x2﹣2x+1
【分析】根据能够运用平方差公式分解因式的多项式必须是二项式，两项都能写成平方的形式，且符号相反进行分析即可．
【解答】解：A、不能用平方差分解因式，故此选项不合题意；
B、能用平方差分解因式，故此选项符合题意；
C、不能用平方差分解因式，故此选项不合题意；
D、不能用平方差分解因式，故此选项不合题意；
故选：B．
3．（3分）如图直线AB，CD被EF所截，图中标注的角中是同位角的是（　　）

A．∠1与∠3 B．∠2与∠6 C．∠3与∠8 D．∠4与∠7
【分析】根据同位角的概念解答即可．
【解答】解：同位角是∠4与∠7，
故选：D．
4．（3分）如图△ABC中，∠1=∠2，∠ABC=70°，则∠BDC的度数是（　　）

A．110° B．115° C．120° D．130°
【分析】根据三角形内角和定理即可求出答案．
【解答】解：∵∠ABC=70°，
∴∠DBC=∠ABC﹣∠1，
∵∠1=∠2，
∴∠BDC=180°﹣∠DBC﹣∠2
=180°﹣（70°﹣∠1）﹣∠2
=110°
故选：A．
5．（3分）若am=3，an=2，则a2m+n等于（　　）
A．11 B．12 C．16 D．18
【分析】根据am•an=a m+n（m，n是正整数），（am）n=amn（m，n是正整数）把a2m+n变为（am）2•an进行计算即可．
【解答】解：a2m+n=a2m•an=（am）2•an=9×2=18，
故选：D．
6．（3分）如图在Rt△ABC中，∠B=90°，∠ACB=60°，EF∥GH，若∠1=58°，则∠2的度数是（　　）

A．22° B．26° C．28° D．32°
【分析】依据三角形内角和定理，可得∠A的度数，再根据三角形外角性质以及平行线的性质，即可得到∠2的度数．
【解答】解：∵Rt△ABC中，∠B=90°，∠ACB=60°，
∴∠A=30°，
由三角形外角性质，可得∠ADF=∠1﹣∠A=28°，
又∵EF∥GH，
∴∠2=∠ADF=28°，
故选：C．
7．（3分）已知a=（﹣0.3）2，b=﹣3﹣2，，比较a，b，c的大小（　　）
A．a＜b＜c B．b＜a＜c C．a＜c＜b D．c＜a＜b
【分析】直接利用负指数幂的性质分别化简得出答案．
【解答】解：∵a=（﹣0.3）2=，
b=﹣3﹣2=﹣，
=9，
∴c＞a＞b．
故选：B．
8．（3分）450﹣299的计算结果是（　　）
A．833 B．822 C．811 D．89
【分析】首先将算式中的两项化为同底数幂，然后再逆用同底数幂的乘法法则将2100化为2×299，然后计算即可．
【解答】解：450﹣299=2100﹣299
=2×299﹣299
=299
=833
故选：A．
9．（3分）已知如图，长方形ABCD绕点D顺时针旋转90°形成了长方形EFGD，若AG=m，CE=n，则长方形ABCD的面积是（　　）

A． B． C． D．
【分析】利用旋转的性质得DE=DA，DC=DG，则CD﹣AD=n，CD+AD=m，通过解方程组得到CD=，AD=，然后计算矩形ABCD的面积即可．
【解答】解：∵长方形ABCD绕点D顺时针旋转90°形成了长方形EFGD，
∴DE=DA，DC=DG，
而CE=n，AG=m，
∴CD﹣AD=n，CD+AD=m，
∴CD=，AD=，
∴长方形ABCD的面积=CD•AD=•=．
故选：B．
10．（3分）如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，BO的延长线交CE于点E，记∠BAC=∠1，∠BEC=∠2，则以下结论①∠1=2∠2，②∠BOC=3∠2，③∠BOC=90°+∠1，④∠BOC=90°+∠2正确的是（　　）

A．①②③ B．①③④ C．①④ D．①②④
【分析】依据角平分线的性质以及三角形外角性质，即可得到∠1=2∠2，∠BOC=90°+∠1，∠BOC=90°+∠2．
【解答】解：∵CE为外角∠ACD的平分线，BE平分∠ABC，
∴∠DCE=∠ACD，∠DBE=∠ABC，
又∵∠DCE是△BCE的外角，
∴∠2=∠DCE﹣∠DBE，
=（∠ACD﹣∠ABC）
=∠1，故①正确；
∵BO，CO分别平分∠ABC，
∴∠OBC=ABC，∠OCB=∠ACB，
∴∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣（∠ABC+∠ACB）
=180°﹣（180°﹣∠1）
=90°+∠1，故②、③错误；
∵OC平分∠ACB，CE平分∠ACD，
∴∠ACO=∠ACB，∠ACE=ACD，
∴∠OCE=（∠ACB+∠ACD）=×180°=90°，
∵∠BOC是△COE的外角，
∴∠BOC=∠OCE+∠2=90°+∠2，故④正确；
故选：C．

　
二、填空题（本大题共8小题，每小题3分，共24分）
11．（3分）若正多边形的一个外角等于36°，那么这个正多边形的边数是　10　．
【分析】根据正多边形的外角和以及一个外角的度数，求得边数．
【解答】解：正多边形的一个外角等于36°，且外角和为360°，
则这个正多边形的边数是：360°÷36°=10．
故答案为：10．
12．（3分）数0.000001用科学记数法可表示为　1×10﹣6　．
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】解：0.000 001=1×10﹣6．
故答案为：1×10﹣6．
13．（3分）已知94=3a×3b，则a+b=　8　．
【分析】首先把94化为38，再根据同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加进行计算即可．
【解答】解：∵3a×3b=94，
∴3a+b=38，
∴a+b=8，
故答案为：8．
14．（3分）若x2+mx﹣15=（x+3）（x+n），则m﹣n的值为　3　．
【分析】已知等式右边利用多项式乘多项式法则计算，再利用多项式相等的条件求出m与n的值，即可求出m﹣n的值．
【解答】解：∵（x+3）（x+n）=x2+nx+3x+3n=x2+（n+3）x+3n，
∴，
解得：m=﹣2，n=﹣5，
则m﹣n=﹣2+5=3，
故答案为：3．
15．（3分）如图，由直线a∥b得到∠1=∠2的理由是　两直线平行，内错角相等　．

【分析】依据平行线的性质进行判断即可．
【解答】解：由直线a∥b得到∠1=∠2的理由是：两直线平行，内错角相等．
故答案为：两直线平行，内错角相等．
16．（3分）已知：s﹣t=3，则t2+6t﹣s2=　﹣9　．
【分析】根据平方差公式可得t2﹣s2+6t=（s+t）（t﹣s）+6t，把s﹣t=3代入可得原式=﹣3（s+t）+6t=3（t﹣s），再代入即可求解．
【解答】解：∵s﹣t=3，
∴t2﹣s2+6t=（s+t）（t﹣s）+6t
=﹣3（s+t）+6t
=3（t﹣s）
=﹣9，
故答案为：﹣9
17．（3分）22﹣23﹣24﹣25……﹣22017+22018=　12　．
【分析】设S=22﹣23﹣24﹣25……﹣22017+22018，则2S=23﹣24﹣25﹣26……﹣22018+22019，利用2S﹣S可得结论．
【解答】解：设S=22﹣23﹣24﹣25……﹣22017+22018，
∴2S=23﹣24﹣25﹣26……﹣22018+22019，
∴2S﹣S=S=24﹣4﹣22019+22019=16﹣4=12，
即22﹣23﹣24﹣25……﹣22017+22018=12，
故答案为：12．
18．（3分）如图△ABC中，∠A=∠C，∠BDE=∠BED，BD平分∠ABC，若∠CDE=12°，则∠A=　66°　．

【分析】由等腰三角形的三线合一定理可知∠BDC=90°，从而可知∠BDE=∠BED=78°，由三角形的外角和性质可知∠C+∠CDE=∠BED，所以∠A=∠C=66°
【解答】解：∵∠A=∠C，BD平分∠ABC，
∴∠BDC=90°，
∵∠CDE=12°，
∴∠BDE=∠BED=78°，
∵∠C+∠CDE=∠BED，
∴∠C=66°，
∴∠A=∠C=66°
故答案为：66°
三、解答题：（本大题共9小题，共76分.把解答过程写在答题卡相应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明）.
19．（16分）计算：
（1）（﹣2a2bc3）2
（2）（﹣a2）3•（﹣a3）2
（3）（2a﹣b）2﹣a（3a﹣2b）
（4）（2a+b﹣3）（2a﹣b﹣3）
【分析】（1）原式利用幂的乘方与积的乘方运算法则计算即可求出值；
（2）原式利用幂的乘方与积的乘方运算法则计算即可求出值；
（3）原式利用完全平方公式，以及单项式乘以多项式法则计算，去括号合并即可得到结果；
（4）原式利用平方差公式，以及完全平方公式计算即可求出值．
【解答】解：（1）原式=4a4b2c6；
（2）原式=﹣a6•a6=﹣a12；
（3）原式=4a2﹣4ab+b2﹣3a2+2ab=a2﹣2ab+b2；
（4）原式=（2a﹣3）2﹣b2=4a2﹣12a+9﹣b2．
20．（16分）将下列各式分解因式：
（1）2ax2﹣8a
（2）x2﹣6xy+5y2
（3）（2m﹣n）2﹣6n（2m﹣n）+9n2
（4）a2﹣b2+2b﹣1
【分析】（1）利用提取公因式法和平方差公式进行因式分解；
（2）利用十字相乘法进行因式分解；
（3）利用完全平方公式进行因式分解；
（4）利用完全平方公式和平方差公式进行因式分解．
【解答】解：（1）2ax2﹣8a
=2a（x2﹣4）
=2a（x+2）（x﹣2）；

（2）x2﹣6xy+5y2
=（x﹣y）（x﹣5y）；

（3）（2m﹣n）2﹣6n（2m﹣n）+9n2
=（2m﹣n﹣3n）2
=4（m﹣2n）2；

（4）a2﹣b2+2b﹣1
=a2﹣（b﹣1）2
=（a+b﹣1）（a﹣b+1）．
21．（5分）先化简，再求值：（x﹣2）2+2（x﹣2）（x+4）﹣（x﹣3）（x+3），其中x=﹣2．
【分析】原式利用完全平方公式，平方差公式，以及多项式乘多项式法则计算，去括号合并得到最简结果，把x的值代入计算即可求出值．
【解答】解：原式=x2﹣4x+4+2x2+4x﹣16﹣x2+9=2x2﹣3，
当x=﹣2时，原式=8﹣3=5．
22．（5分）已知4m+3×8m+1÷24m+7=16，求m的值．
【分析】直接利用幂的乘方运算法则将原式变形进而结合同底数幂的乘除运算法则计算得出答案．
【解答】解：∵4m+3×8m+1÷24m+7=16，
∴22m+6×23m+3÷24m+7=24，
则2m+6+3m+3﹣（4m+7）=4，
解得：m=2．
23．（6分）如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）．

（1）分别画出△ABC中BC边上的高AH、中线AG．
（2）画出先将△ABC向右平移6格，再向上平移3格后的△DEF．
（3）画一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积的2倍．
【分析】（1）根据三角形的高和中线的定义结合网格作图可得；
（2）根据平移变换的定义和性质作图可得；
（3）由△ABC的面积为3知所作三角形的面积为6，据此结合网格作图可得．
【解答】解：（1）如图所示，AH、AG即为所求；


（2）如图所示，△DEF即为所求；

（3）如图所示，△MNP即为所求．
24．（6分）已知a+2b=1，ab=﹣1，求下列代数式的值：
（1）a2+4b2
（2）（a﹣2b）2
【分析】（1）直接利用完全平方公式将原式变形进而得出答案；
（2）直接利用完全平方公式将原式变形进而得出答案．
【解答】解：（1）∵a+2b=1，ab=﹣1，
∴（a+2b）2=a2+4ab+4b2=1，
∴a2+4b2=1+4=5；

（2）∵a2+4b2=5，
∴（a﹣2b）2=a2﹣4ab+4b2=5+4=9．
25．（6分）将一副直角三角尺BAC和ADE如图放置，其中∠BAC=∠ADE=90°，∠BCA=30°，∠AED=45°，若∠AFD=75°，试判断AE与BC的位置关系，并说明理由．

【分析】根据三角形外角性质，可得∠EAF=30°，再根据∠C=30°，可得∠EAF=∠C，进而判定AE∥BC．
【解答】解：AE与BC平行．理由：
∵∠AFD是△AEF的外角，
∴∠EAF=∠AFD﹣∠E=75°﹣45°=30°，
又∵∠C=30°，
∴∠EAF=∠C，
∴AE∥BC．
26．（8分）阅读下列材料：
“a2≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式．例如：x2+4x+5=x2+4x+4+1=（x+2）2+1
∵（x+2）2≥0，
∴（x+2）2+1≥1，
∴x2+4x+5≥1．
试利用“配方法”解决下列问题：
（1）填空：x2﹣4x+5=（x　﹣2　）2+1；
（2）已知x2+y2=4x﹣2y﹣5，求xy的值；
（3）比较代数式2x2﹣1与4x﹣5的大小．
【分析】（1）根据配方法的方法配方即可；
（2）先配方得到非负数和的形式，再根据非负数的性质得到x、y的值，再代入得到xy的值；
（3）将两式相减，再配方即可作出判断
【解答】解：（1）x2﹣4x+5=（x﹣2）2+1．
故答案是：﹣2；

（2）x2﹣4x+y2+2y+5=0，
（x﹣2）2+（y+1）2=0，
则x﹣2=0，y+1=0，
解得x=2，y=﹣1，
则xy=2×（﹣1）=﹣1；

（3）2x2﹣1﹣（4x﹣5）
=2x2﹣4x+4
=2（x﹣1）2+2，
∵（x﹣1）2≥0，
∴2（x﹣1）2+2＞0，
∴2x2﹣1＞4x﹣5．
27．（8分）在正方形ABCD中，∠C=∠D=90°，点E、F分别是边CD、BC上的中点，点P是一动点．记∠DEP=∠1，∠BFP=∠2，∠EPF=∠α．

（1）如图1，若点P运动到线段AD中点时，∠α=　45°　，∠1+∠2=　90°　．
（2）如图2，若点P在线段AD上运动时，∠1、∠2和∠α之间有何关系？
（3）当点P在直线AD上（在线段AD之外且PE与PF不重合）运动时，∠1、∠2和∠α之间又有何关系？说明理由．
【分析】（1）只要证明△PDE是等腰直角三角形，四边形CDPF是矩形即可解决问题；
（2）连接PC．利用三角形的外角的性质即可解决问题；
（3）分三种情形分别求解即可；
【解答】解：（1）如图1中，

∵四边形ABCD是正方形，
∴∠D=90°，AD=BC=DC，AD∥BC，
∵PA=PD，DE=EC，BF=FC，
∴PD=DE，
∴∠1=45°，
∵PD=FC，PD∥FC，
∴四边形CDPF是平行四边形，
∵∠D=90°，
∴四边形CDPF是矩形，
∴PF∥CD，∠PFC=90°，
∴∠α=∠1=45°，∠2=90°，
故答案为45°，90°．

（2）如图2中，连接PC．

∵∠1=∠EPC+∠ECP，∠2=∠FPC+∠FCP，
∴∠1+∠2=∠EPC+∠FPC+∠ECP+∠FCP=∠α+90°．

（3）如图：

①当点P在线段DA的延长线上时，由（2）可知：∠1+∠2=∠α+90°．
②当点P在线段AD的延长线上且在直线EF的上方时，
∵∠2=∠α+∠PKF，∠PKF=90°+∠KEC=90°+∠1，
∴∠2=∠α+∠1+90°．
③当点P在直线EF的下方时，设PF交CD于K．
∵∠2=90°+∠FKC=90°+∠PKE=90°+（∠1﹣∠α），
∴∠2=90°+∠1﹣∠α．