初中数学人教版七年级下册第五章 相交线与平行线综合与测试习题ppt课件

这是一份初中数学人教版七年级下册第五章 相交线与平行线综合与测试习题ppt课件，共19页。PPT课件主要包含了答案显示，见习题等内容，欢迎下载使用。

1．如图，AB∥CD，探讨∠APC与∠PAB，∠PCD的数量关系，并请你说明成立的理由．
【点拨】过点P作直线与AB(或CD)平行，为说明角之间的数量关系创造条件．
解：∠APC＝∠PAB＋∠PCD.理由：如图，过点P作PE∥AB.∵AB∥CD，∴PE∥AB∥CD.∴∠PAB＝∠APE，∠PCD＝∠CPE.∵∠APC＝∠APE＋∠CPE，∴∠APC＝∠PAB＋∠PCD.
2．若平行线EF，MN与相交线AB，CD相交成如图所示的图形，则共得出同旁内角多少对？
【点拨】从原图中分离出“三线”，分别计数后相加即可．
解：如图，将给出的图形分离为8个“三线八角”的基本图形，由每个基本图形都有2对同旁内角，知共有16对同旁内角．
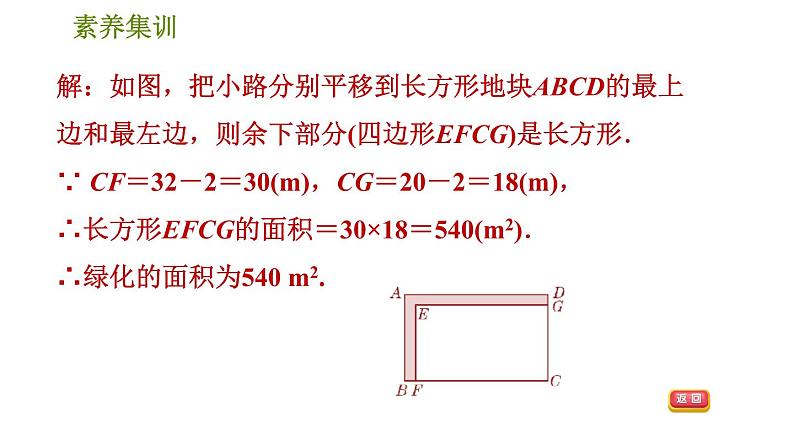
3．如图，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的小路，余下部分绿化，小路的宽为2 m．绿化的面积为多少？
【点拨】把小路“平移”后，求绿化面积可转化为求长方形的面积．
解：如图，把小路分别平移到长方形地块ABCD的最上边和最左边，则余下部分(四边形EFCG)是长方形．∵ CF＝32－2＝30(m)，CG＝20－2＝18(m)，∴长方形EFCG的面积＝30×18＝540(m2)．∴绿化的面积为540 m2.
4．如图，由点O引出六条射线OA，OB，OC，OD，OE，OF，且AO⊥OB，OF平分∠BOC，OE平分∠AOD.若∠EOF＝170°，求∠COD的度数．
5．【中考·武汉】如图，点A，B，C，D在一条直线上，CE与BF交于点G，∠A＝∠1，CE∥DF.求证∠E＝∠F.
【点拨】由∠A＝∠1可得AE∥BF.由AE∥BF无法直接证得∠E＝∠F，可以把∠2作为“桥梁”，问题得证．
证明：∵∠A＝∠1，∴AE∥BF.∴∠E＝∠2.∵CE∥DF，∴∠2＝∠F.∴∠E＝∠F.
6．【2020·枣庄】一副直角三角尺如图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，则∠DBC的度数为(　　)A．10°B．15°C．18°D．30°
证明：由对顶角相等，得∠CNF＝∠END.∵∠CNF＋∠BMN＝180°，∴∠END＋∠BMN＝180°.∴AB∥CD.∴∠EMB＝∠END.又∵∠1＝∠2，∴∠END＋∠2＝∠EMB＋∠1，即∠ENQ＝∠EMP.∴MP∥NQ.
7．如图，直线AB，CD被EF所截，∠1＝∠2，∠CNF＋∠BMN＝180°.求证：AB∥CD，MP∥NQ.
8．如图，直线l1∥l2，直线l3交l1于点C，交l2于点D，P是线段CD上的一个动点．当点P在线段CD上运动时，探究∠1，∠2，∠3之间的关系．
【点拨】解决动点问题时，常常需要分类讨论．本题中点P在线段CD上运动，应考虑到点P与点C，D重合的情况．
解：当点P在C，D之间时，过点P作PE∥AC，则PE∥BD，如图①所示．∵PE∥AC, ∴∠APE＝∠1.∵PE∥BD，∴∠BPE＝∠3.∵∠2＝∠APE＋∠BPE，∴∠2＝∠1＋∠3.当点P与点C重合时，∠1＝0°，如图②所示．∵l1∥l2，∴∠2＝∠3.
∵∠1＝0°， ∴∠2＝∠1＋∠3.当点P与点D重合时，∠3＝0°，如图③所示．∵l1∥l2，∴∠2＝∠1.∵∠3＝0°，∴∠2＝∠1＋∠3.综上所述，当点P在线段CD上运动时，∠1，∠2，∠3之间的关系为∠2＝∠1＋∠3.
9．如图，点O在直线AC上，OE，OF分别平分∠AOB，∠BOC.(1)若∠AOB＝120°，求∠EOF的度数；