初中数学北师大版八年级下册第三章 图形的平移与旋转综合与测试习题课件ppt

这是一份初中数学北师大版八年级下册第三章 图形的平移与旋转综合与测试习题课件ppt，共34页。PPT课件主要包含了①②④⑤，答案呈现，习题链接等内容，欢迎下载使用。
下面给出的五种运动属于平移的是________(填序号)．①急刹车的汽车车身在地面上的运动；②沿直线行驶的汽车车身的运动；③时钟分针的运动；④高层建筑的电梯的运动；⑤小球从高处向下坠落(球不转动)．
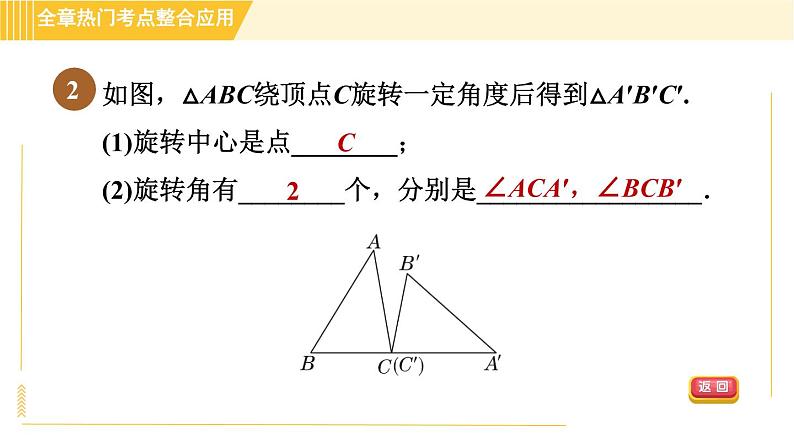
如图，△ABC绕顶点C旋转一定角度后得到△A′B′C′.(1)旋转中心是点________；(2)旋转角有________个，分别是_________________．
∠ACA′，∠BCB′
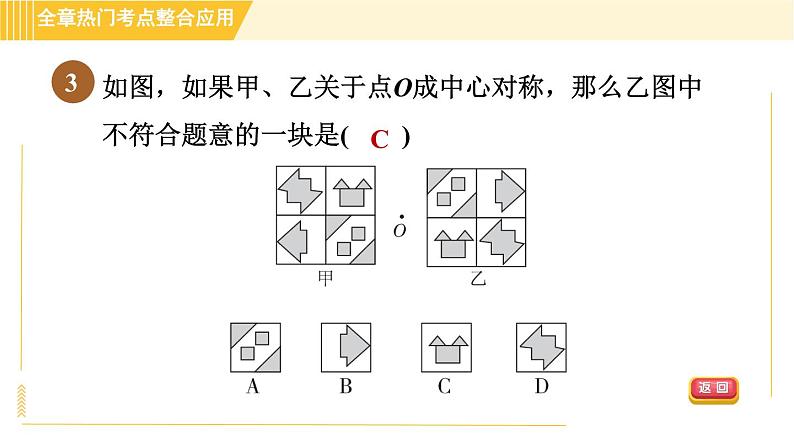
如图，如果甲、乙关于点O成中心对称，那么乙图中不符合题意的一块是(　　)
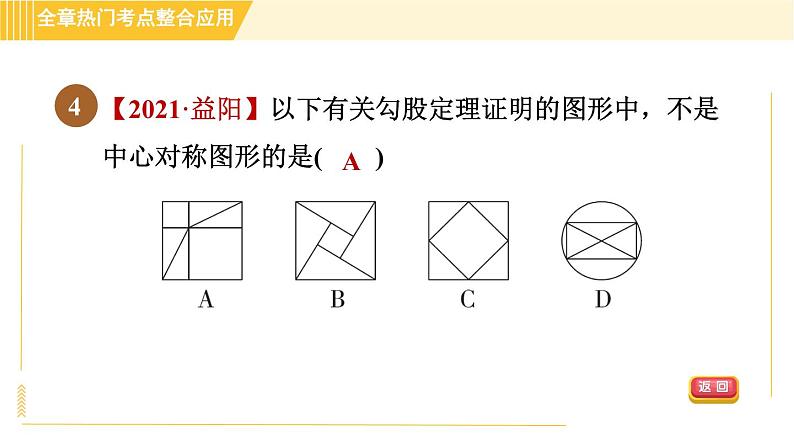
【2021·益阳】以下有关勾股定理证明的图形中，不是中心对称图形的是(　　)
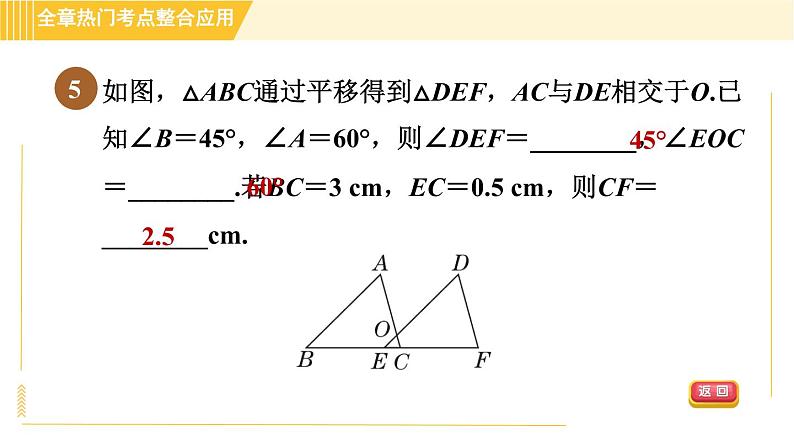
如图，△ABC通过平移得到△DEF，AC与DE相交于O.已知∠B＝45°，∠A＝60°，则∠DEF＝________，∠EOC＝________.若BC＝3 cm，EC＝0.5 cm，则CF＝________cm.
如图，点O是等边三角形ABC内一点，将△BOC绕点C按顺时针方向旋转60°得到△ADC，连接OD.已知∠AOB＝110°.
(1)求证：△COD是等边三角形；
证明：由旋转的性质得CO＝CD，∠OCD＝60°，∴△COD是等边三角形．
(2)当α＝150°时，试判断△AOD的形状，并说明理由；
解：当α＝150°，即∠BOC＝150°时，△AOD是直角三角形．理由如下：由旋转的性质得∠ADC＝∠BOC＝150°.∵△COD是等边三角形，∴∠ODC＝60°.∴∠ADO＝90°，即△AOD是直角三角形．
(3)探究：当α为多少度时，△AOD是等腰三角形？
解：①当AO＝AD时，∠AOD＝∠ADO.∵△COD是等边三角形，∴∠COD＝60°.∴∠AOD＝360°－∠AOB－∠COD－α＝360°－110°－60°－α＝190°－α.∵∠ADC＝∠BOC＝α，∴∠ADO＝∠ADC－∠CDO＝α－60°.∴190°－α＝α－60°，解得α＝125°.
②当OA＝OD时，∠OAD＝∠ADO.∵∠AOD＝190°－α，∠ADO＝α－60°，∴∠OAD＝180°－(∠AOD＋∠ADO)＝50°.∴α－60°＝50°，解得α＝110°.③当OD＝AD时，∠OAD＝∠AOD，即190°－α＝50°，∴α＝140°.综上所述，当α为125°、110°或140°时，△AOD是等腰三角形．
如图，在一块平行四边形的菜地中，有一口圆形的水井，现在张大爷要在菜地上修建一条笔直的小路将菜地面积二等分以播种不同的蔬菜，且要使水井在小路上，以便有利于对两块地进行浇灌，请你帮助张大爷画出小路修建的位置．
解：如图，小路应修建在直线AB上．
【2021·桂林】如图，在平面直角坐标系中，线段AB的两个端点的坐标分别是A(－1，4)，B(－3，1)．
(1)画出线段AB向右平移4个单位后的线段A1B1；
解：如图，线段A1B1即为所求．
(2)画出线段AB绕原点O旋转180°后的线段A2B2.
解：如图，线段A2B2即为所求．
如图，在六边形ABCDEF中，已知AB∥DE，AF∥CD，BC∥FE，AB＝DE，AF＝CD，BC＝FE，FD⊥BD，FD＝24 cm，BD＝18 cm，你能求出六边形ABCDEF的面积吗？
解：能．如图，将△DEF竖直向上平移，使点D与点B重合，点E与点A重合，得到△BAG，将△BCD水平向左平移，使点B与点G重合，点D与点F重合，点C与点A重合，得到△GAF.
则△DEF≌△BAG，△BCD≌△GAF，GB∥FD，GF∥BD.∴S△DEF＝S△BAG，S△BCD＝S△GAF.易得四边形BDFG是长方形，∴S六边形ABCDEF＝S△DEF＋S△BCD＋S四边形BDFA＝S△BAG＋S△GAF＋S四边形BDFA＝S四边形BDFG＝FD·BD＝24×18＝432(cm2)．
证明：如图，延长BE交AC于点F(即把△ABE沿AD翻折得到△AFE)．∵AD平分∠BAC，∴∠BAE＝∠FAE.∵BE⊥AD，∴∠AEB＝∠AEF＝90°.
如图①，△ABC与△DCE均为等腰直角三角形，DC与AB交于点M，CE与AB交于点N，以点C为中心，将△ACM逆时针旋转90°，得到△BCM′.
(1)求证：AM2＋BN2＝MN2.
证明：连接M′N.∵△ABC和△DCE均为等腰直角三角形，∴∠ACB＝90°，∠DCE＝45°，∠A＝∠CBA＝45°.∴∠ACM＋∠BCN＝45°.∵△BCM′是由△ACM旋转得到的，∴∠BCM′＝∠ACM，CM＝CM′，AM＝BM′，∠CBM′＝∠A＝45°.
∴∠M′CN＝∠BCM′＋∠BCN＝∠ACM＋∠BCN＝45°，∠NBM′＝∠CBA＋∠CBM′＝45°＋45°＝90°.∴∠M′CN＝∠MCN.
(2)如图②，在四边形ABCD中，∠BAD＝45°，∠BCD＝90°，CA平分∠BCD.若BC＝4，CD＝3，则对角线AC的长度为多少？
解：如图，将△ADC绕点A顺时针旋转90°得到△AD′C′，连接CC′，BD.由旋转的性质知AC′＝AC，AD＝AD′，C′D′＝CD＝3，∠CAC′＝∠DAD′＝90°，∠AC′D′＝∠ACD，∴△AC′C是等腰直角三角形．∴∠AC′C＝∠ACC′＝45°.
∵∠DAD′＝90°，∠BAD＝45°，∴∠BAD′＝45°.
如图，P是正方形ABCD的边CD上一点，∠BAP的平分线交边BC于点Q.求证：AP＝DP＋BQ.
证明：如图，将△ABQ绕点A逆时针旋转90°后得到△ADE.∴∠EAQ＝90°，△AED≌△AQB.∴∠E＝∠AQB，DE＝BQ，∠ADE＝∠B＝90°.∴E，D，P三点共线．
又∵∠BAP的平分线交边BC于点Q，AD∥BC，∴∠BAQ＝∠PAQ，∠DAQ＝∠AQB.∴∠PAE＝90°－∠PAQ＝90°－∠BAQ＝∠DAQ＝∠AQB＝∠E.∴AP＝PE＝DP＋DE＝DP＋BQ.