初中沪教版 (五四制)第十四章 三角形综合与测试同步测试题

这是一份初中沪教版 (五四制)第十四章 三角形综合与测试同步测试题，共31页。试卷主要包含了如图，直线l1l2，被直线l3，如图，下列三角形与下图全等的三角形是等内容，欢迎下载使用。
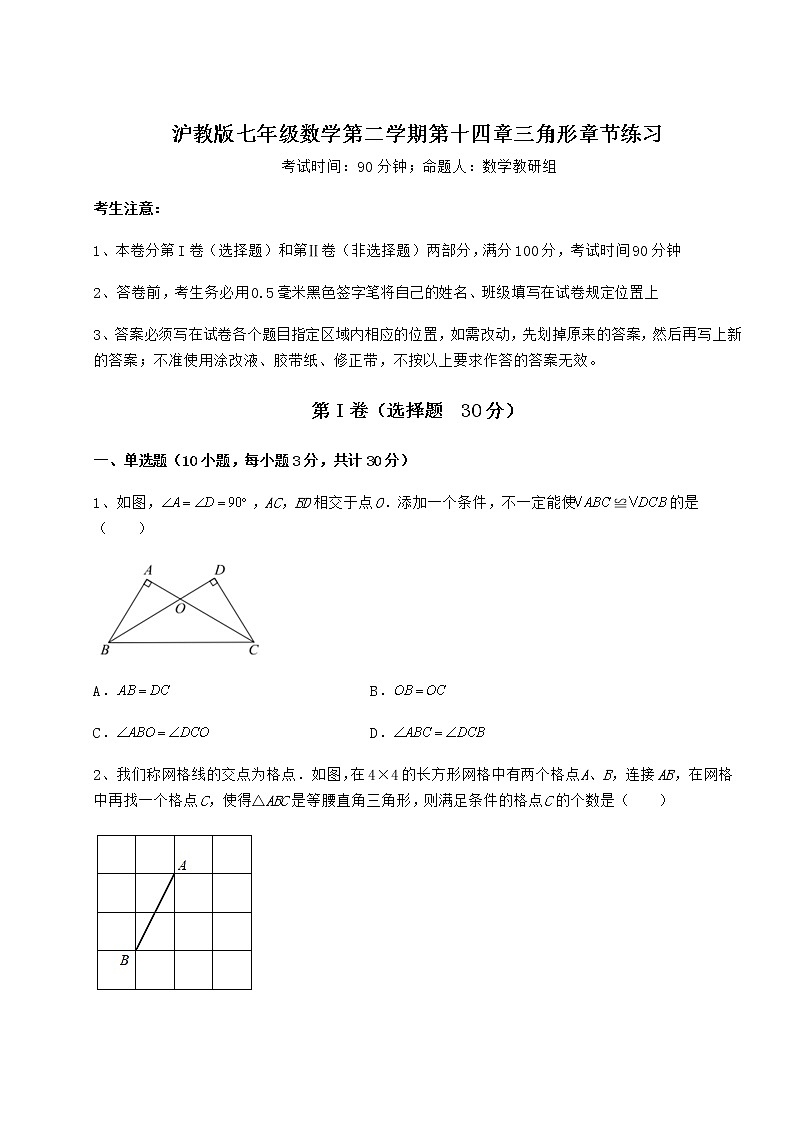
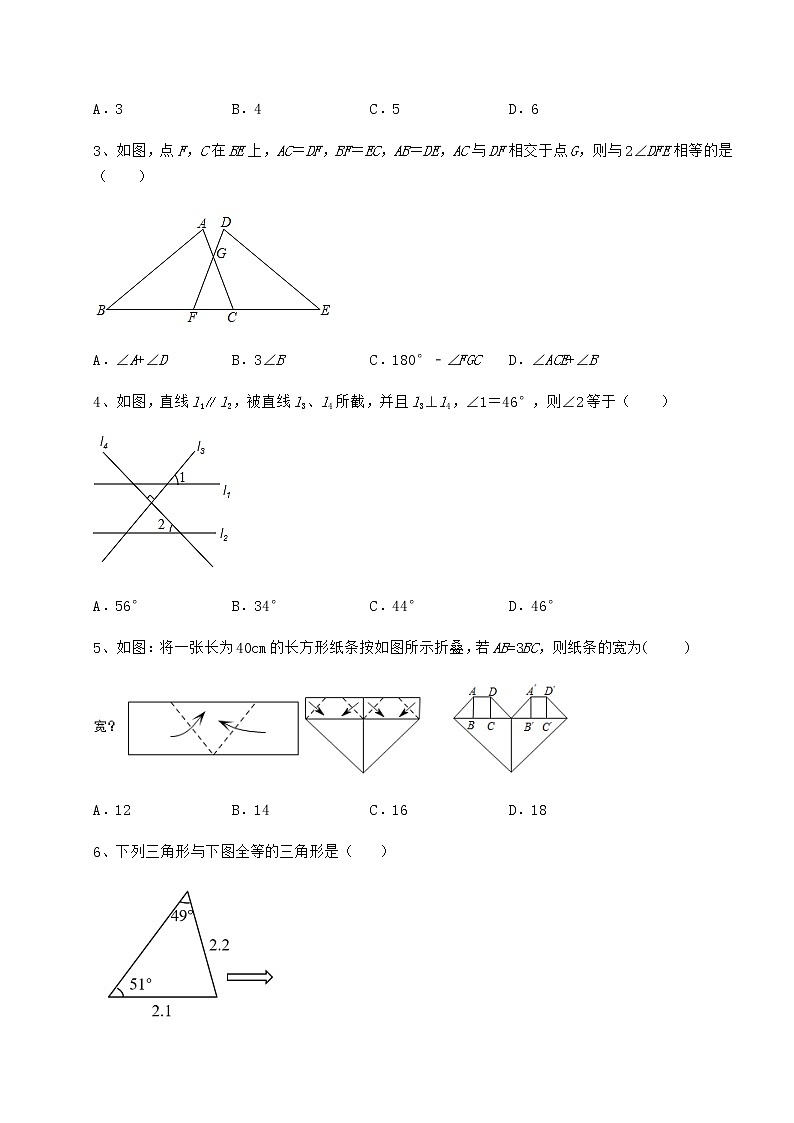
沪教版七年级数学第二学期第十四章三角形章节练习 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，，AC，BD相交于点O．添加一个条件，不一定能使≌的是（    ）A． B．C． D．2、我们称网格线的交点为格点．如图，在4×4的长方形网格中有两个格点A、B，连接AB，在网格中再找一个格点C，使得△ABC是等腰直角三角形，则满足条件的格点C的个数是（　　）A．3 B．4 C．5 D．63、如图，点F，C在BE上，AC＝DF，BF＝EC，AB＝DE，AC与DF相交于点G，则与2∠DFE相等的是（　　）A．∠A+∠D B．3∠B C．180°﹣∠FGC D．∠ACE+∠B4、如图，直线l1l2，被直线l3、l4所截，并且l3⊥l4，∠1＝46°，则∠2等于（　　）A．56° B．34° C．44° D．46°5、如图：将一张长为40cm的长方形纸条按如图所示折叠，若AB=3BC，则纸条的宽为(     ) A．12 B．14 C．16 D．186、下列三角形与下图全等的三角形是（    ）A． B． C． D．7、如图，等腰△ABC中，AB＝AC，点D是BC边中点，则下列结论不正确的是（   ）A．B＝C B．AD⊥BC C．BAD＝CAD D．AB＝2BC8、如图，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形．他的依据是（    ）A． B． C． D．9、已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为（    ）A．10 B．15 C．17 D．1910、若等腰三角形的一个外角是70°，则它的底角的度数是（    ）A．110° B．70° C．35° D．55°第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，点C是线段AB的中点，．请你只添加一个条件，使得≌．（1）你添加的条件是______；（要求：不再添加辅助线，只需填一个答案即可）（2）依据所添条件，判定与全等的理由是______．2、如图，BD，CE是等边三角形ABC的中线，BD，CE交于点F，则______°．3、等腰，，底角为70°，点在边上，将分成两个三角形，当这两个三角形有一个是以为腰的等腰三角形时，则的度数是______．4、如图，△ABC中，AB平分∠DAC，AB⊥BC，垂足为B，若∠ADC与∠ACB互补，BC＝5，则CD的长为_________．5、如图，AB，CD相交于点O，，请你补充一个条件，使得，你补充的条件是______．三、解答题（10小题，每小题5分，共计50分）1、如图1，点O是线段AD的中点，分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD，连接AC和BD，相交于点E，连接BC．（1）求证DOB≌AOC；（2）求∠CEB的大小；（3）如图2，OAB固定不动，保持△OCD的形状和大小不变，将OCD绕点O旋转（OAB和OCD不能重叠），求∠CEB的大小．2、如图，△ABC是等边三角形，点D、E、F分别同时从A、B、C以同样的速度沿AB、BC、CA方向运动，当点D运动到点B时，三个点都停止运动．（1）在运动过程中△DEF是什么形状的三角形，并说明理由；（2）若运动到某一时刻时，BE=4，∠DEC=150°，求等边△ABC的周长；3、如图，在中，点D、E分别在边AB、AC上，BE与CD交于点F，，，．求和的度数．4、已知：如图，点D为BC的中点，，求证：是等腰三角形．5、如图，是等边三角形，，分别交AB，AC于点D，E．（1）求证：是等边三角形；（2）点F在线段DE上，点G在外，，，求证：．6、如图，为等边三角形，D是BC中点，，CE是的外角的平分线．求证：．7、 “三等分角”是被称为几何三大难题的三个古希腊作图难题之一．如图1所示的“三等分角仪”是利用阿基米德原理做出的．这个仪器由两根有槽的棒PA，PB组成，两根棒在P点相连并可绕点P旋转，C点是棒PA上的一个固定点，点A，O可在棒PA，PB内的槽中滑动，且始终保持OA＝OC＝PC．∠AOB为要三等分的任意角．则利用“三等分角仪”可以得到∠APB ＝∠AOB．我们把“三等分角仪”抽象成如图2所示的图形，完成下面的证明．已知：如图2，点O，C分别在∠APB的边PB，PA上，且OA＝OC＝PC．求证：∠APB ＝∠AOB．8、如图，是的中线，分别过点、作及其延长线的垂线，垂足分别为、．（1）求证：；（2）若的面积为8，的面积为6，求的面积．9、如图，将△ABC绕点A逆时针旋转得到△ADE，点D在BC上，已知∠B＝70°，求∠CDE的大小．10、如图，是的角平分线，于点．（1）用尺规完成以下基本作图：过点作于点，连接交于点．（不写作法，保留作图痕迹）（2）在（1）中所作的图形中，求证：． -参考答案-一、单选题1、C【分析】直接利用直角三角形全等的判定定理（定理）即可判断选项；先根据等腰三角形的性质可得，再根据三角形全等的判定定理（定理）即可判断选项；直接利用三角形全等的判定定理（定理）即可判断选项，由此即可得出答案．【详解】解：当添加条件是时，在和中，，，则选项不符题意；当添加条件是时，，在和中，，，则选项不符题意；当添加条件是时，在和中，，，则选项不符题意；当添加条件是时，不一定能使，则选项符合题意；故选：C．【点睛】本题考查了三角形全等的判定、等腰三角形的性质，熟练掌握三角形全等的判定方法是解题关键．2、A【分析】根据题意，结合图形，分两种情况讨论：①AB为等腰直角△ABC底边；②AB为等腰直角△ABC其中的一条腰．【详解】解：如图：分情况讨论：①AB为等腰直角△ABC底边时，符合条件的格点C点有0个；②AB为等腰直角△ABC其中的一条腰时，符合条件的格点C点有3个．故共有3个点，故选：A．【点睛】本题考查了等腰三角形的性质和判定；解答本题关键是根据题意，画出符合实际条件的图形，数形结合的思想是数学解题中很重要的解题思想．3、C【详解】由题意根据等式的性质得出BC＝EF，进而利用SSS证明△ABC与△DEF全等，利用全等三角形的性质得出∠ACB＝∠DFE，最后利用三角形内角和进行分析解答．【分析】解：∵BF＝EC，∴BF+FC＝EC+FC，∴BC＝EF，在△ABC与△DEF中，，∴△ABC≌△DEF（SSS），∴∠ACB＝∠DFE，∴2∠DFE＝180°﹣∠FGC，故选：C．【点睛】本题考查全等三角形的判定与性质，其中全等三角形的判定方法有：SSS；SAS；ASA；AAS；以及HL（直角三角形的判定方法）．4、C【分析】依据l1∥l2，即可得到∠3＝∠1＝46°，再根据l3⊥l4，可得∠2＝90°﹣46°＝44°．【详解】解：如图：∵l1∥l2，∠1＝46°，∴∠3＝∠1＝46°，又∵l3⊥l4，∴∠2＝90°﹣46°＝44°，故选：C．【点睛】本题考查了平行线性质以及三角形内角和，平行线的性质：两直线平行，同位角相等以及三角形内角和是180°．5、B【分析】如图，延长NO交AD的延长线于点P，设BC=x，则AB=3x，利用折叠的性质和等腰直角三角形的性质可表示出纸条的宽MO，NO的长，从而可表示出纸条的长2PN的长，然后根据长方形纸条的长为40，可得到关于x的方程，解方程求出x的值，即可求出纸条的宽．【详解】解：如图，延长NO交AD的延长线于点P， 设BC=x，则AB=3x， ∵折叠， ∴AB=BM=CO=CD=PO=3x， ∴纸条的宽为：MO=NO=3x+3x+x=7x， ∴纸条的长为：2PN=2（7x+3x）=20x=40 解得：x=2， ∴纸条的宽NO=7×2=14． 故答案为：B．【点睛】此题考查了折叠的性质，等腰直角三角形的性质，一元一次方程应用题，解题的关键是正确分析题目中的等量关系列出方程求解．6、C【分析】根据已知的三角形求第三个内角的度数，由全等三角形的判定定理即可得出答案．【详解】由题可知，第三个内角的度数为，A.只有两边，故不能判断三角形全等，故此选项错误；B.两边夹的角度数不相等，故两三角形不全等，故此选项错误；C.两边相等且夹角相等，故能判断两三角形全等，故此选项正确；D. 两边夹的角度数不相等，故两三角形不全等，故此选项错误．故选：C．【点睛】本题考查全等三角形的判定，掌握全等三角形的判定定理是解题的关键．7、D【分析】根据等腰三角形的等边对等角的性质及三线合一的性质判断．【详解】解：∵AB＝AC，点D是BC边中点，∴B＝C，AD⊥BC，BAD＝CAD，故选：D．【点睛】此题考查了等腰三角形的性质：等边对等角，三线合一，熟记等腰三角形的性质是解题的关键．8、C【分析】根据题意，可知仍可辨认的有1条边和2个角，且边为两角的夹边，即可根据来画一个完全一样的三角形【详解】根据题意可得，已知一边和两个角仍保留，且边为两角的夹边，根据两个三角形对应的两角及其夹边相等，两个三角形全等，即故选C【点睛】本题考查了三角形全等的性质与判定，掌握三角形的判定方法是解题的关键．9、C【分析】等腰三角形两边的长为3和7，具体哪条是底边，哪条是腰没有明确说明，因此要分两种情况讨论．【详解】解：①当腰是3，底边是7时，3+3＜7，不满足三角形的三边关系，因此舍去．②当底边是3，腰长是7时，3+7＞7，能构成三角形，则其周长＝3+7+7＝17．故选：C．【点睛】本题考查了等腰三角形的性质和三角形的三边关系，解题时注意：若没有明确腰和底边，则一定要分类进行讨论，还应验证各种情况是否能构成三角形，这是解题的关键．10、C【分析】先求出与这个外角相邻的内角的度数为，再根据三角形的内角和定理即可得．【详解】解：等腰三角形的一个外角是，与这个外角相邻的内角的度数为，这个等腰三角形的顶角的度数为，底角的度数为，故选：C．【点睛】本题考查了等腰三角形、三角形的内角和定理等知识点，判断出等腰三角形的顶角的度数为是解题关键．二、填空题1、AD=CE（或∠D=∠E或∠ACD=∠B）（答案不唯一）    SAS    【分析】（1）由已知条件可得两个三角形有一组对应边相等，一组对应角相等，根据三角形全等的判定方法添加条件即可；（2）根据添加的条件，写出判断的理由即可．【详解】解：（1）添加的条件是：AD=CE（或∠D=∠E或∠ACD=∠B）故答案为：AD=CE（或∠D=∠E或∠ACD=∠B）（2）若添加：AD=CE∵点C是线段AB的中点，∴AC=BC∵∴ ∴≌(SAS)故答案为：SAS【点睛】本题主要考查了添加条件判断三角形全等，熟练掌握全等三角形的判断方法是解答本题的关键．2、120【分析】等边三角形中线与角平分线合一，有，，由可求得结果．【详解】解：∵是等边三角形∴∵BD，CE是等边三角形ABC的中线∴又∵∴故答案为：．【点睛】本题考查了等边三角形的性质，角度的计算．解题的关键在于熟练利用等边三角形三线合一的性质．3、100°或110°【分析】画出图形，分两种情况考虑：AD=BD时，则∠ABD=∠A，由三角形内角和可求得∠ADB的度数；BD=BC时，则∠BDC=∠C=70°，从而可求得∠ADB的度数．【详解】∵AB=AC，底角为70°∴∠ABC=∠C=70°，∠A=180°−(∠ABC+∠C)=40° 当AD=BD时，如图1，则∠ABD=∠A=40°∴∠ADB=180°−(∠A+∠ABD)=180°−80°=100°当BD=BC时，如图2，则∠BDC=∠C=70°∴∠ADB=180°−∠BDC=180°−70°=110°综上所述，∠ADB的度数为100°或110°【点睛】本题考查了等腰三角形的性质、三角形内角和定理等知识，涉及分类讨论，关键是等腰三角形的性质，另外要注意分类讨论．4、10【分析】构造，再证得，求得EB=BC,再通过等量代换、等角的补角相等求得∠E=∠CDE，则CE=2BC=10．【详解】解：延长AD.和CB交于点E.∵AB平分∠DAC∴∠EAB=∠CAB又∵∴∠ABE=∠ABC又∵AB=AB∴∴BC=EB=5，∠E=∠ACB， 又∵∴∠ACB=∠CDE∴∠E=∠CDE∴.CD=CE又∵CE=2BC=10∴CD=10故答案为：10．【点睛】本题考查了全等三角形的性质和判定，等角的补角相等，能根据全等三角形的性质找到角与角之间的关系是解答此题的关键．5、（答案不唯一）【分析】在与中，已经有条件： 所以补充可以利用证明两个三角形全等.【详解】解：在与中， 所以补充： 故答案为：【点睛】本题考查的是全等三角形的判定，掌握“利用边边边公理证明两个三角形全等”是解本题的关键.三、解答题1、（1）见详解；（2）120°；（2）120°．【分析】（1）如图1，根据等边三角形的性质得到OD=OC=OA=OB，∠COD=∠AOB=60°，则利用根据“SAS”判断△AOC≌△BOD；（2）利用△AOC≌△BOD得到∠CAO=∠DBO，然后根据三角形内角和可得到∠AEB=∠AOB=60°，即可求出答案；（3）如图2，与（1）的方法一样可证明△AOC≌△BOD；则∠CAO=∠DBO，然后根据三角形内角和可求出∠AEB=∠AOB=60°，即可得到答案．【详解】（1）证明：如图1，∵△ODC和△OAB都是等边三角形，∴OD=OC=OA=OB，∠COD=∠AOB=60°，∴∠BOD=∠AOC=120°，在△AOC和△BOD中∴△AOC≌△BOD；（2）解：∵△AOC≌△BOD，∴∠CAO=∠DBO，∵∠1=∠2，∴∠AEB=∠AOB=60°，∴；（3）解：如图2，∵△ODC和△OAB都是等边三角形，   ∴OD=OC=OA=OB，∠COD=∠AOB=60°，∴∠AOB+∠BOC=∠COD+∠BOC，即∠AOC=∠BOD，在△AOC和△BOD中∴△AOC≌△BOD；∴∠CAO=∠DBO，∵∠1=∠2，∴∠AEB=∠AOB=60°，∴；即∠CEB的大小不变．【点睛】本题考查了几何变换综合题：熟练掌握旋转的性质、等边三角形的性质和全等三角形的判定与性质；利用类比的方法解决（3）小题．2、（1）△DEF是等边三角形，理由见解析（2）等边△ABC的周长为【分析】（1）利用△DEF是等边三角形的性质以及三点的运动情况，求证和，进而证明，最后即可说明△DEF是等边三角形．（2）利用题（1）的条件即∠DEC=150°，得出是含角的直角三角形，求出，最后求解出等边△ABC的长，最后即可求出等边△ABC的周长．【详解】（1）解：△DEF是等边三角形，证明：由点D、E、F的运动情况可知：，△ABC是等边三角形，,，,，在与中， ，，同理可证，进而有，，故△DEF是等边三角形．（2）解：由（1）可知△DEF是等边三角形，且，，，，，， 在中，，，， ，等边△ABC的周长为．【点睛】本题主要是考查了全等三角形的性质及判定、等边三角形的判定及性质和含角直角三角形的性质，熟练利用等边三角形的性质，找到相等条件，进而证明全等三角形，综合利用全等三角形以及含角直角三角形的性质，求出对应边长，是解决该题的关键．3、87°，40°【分析】根据三角形外角的性质可得，，代入计算即可求出，再根据三角形内角和定理求解即可．【详解】解：∵，，∴，∵，∴．【点睛】本题考查了三角形内角和和外角的性质，解题关键是准确识图，理清角之间的关系，准确进行计算．4、证明见解析【分析】过点D作，交AB于点M，过点D做，交AC于点N，根据角平分线性质，得；根据全等三角形的性质，通过证明，通过证明，得，结合等腰三角形的性质，即可完成证明．【详解】如下图，过点D作，交AB于点M，过点D做，交AC于点N∵∴ 直角和直角中 ∴ ∴∵点D为BC的中点，∴ 直角和直角中 ∴∴ ∵， ∴，即是等腰三角形．【点睛】本题考查了角平分线、三角形中线、全等三角形、等腰三角形的知识；解题的关键是熟练掌握角平分线、三角形中线，全等三角形的性质，从而完成求解．5、（1）见详解；（2）见详解【分析】（1）由题意易得，然后根据平行线的性质可得，进而问题可求证；（2）连接AG，由题意易得AB=AC，然后可知△ABF≌△ACG，则有AF=AG，进而可得∠FAG=60°，最后问题可求证．【详解】证明：（1）∵是等边三角形，∴，∵DE∥BC，∴，∴，∴是等边三角形；（2）连接AG，如图所示：∵是等边三角形，∴，AB=AC，∵，，∴△ABF≌△ACG（SAS），∴，∵，∴，∴是等边三角形，∴．【点睛】本题主要考查全等三角形及等边三角形的性质与判定，熟练掌握全等三角形及等边三角形的性质与判定是解题的关键．6、证明见解析.【分析】过D作DG∥AC交AB于G，由等边三角形的性质和平行线的性质得到∠BDG＝∠BGD＝60°，于是得到△BDG是等边三角形，再证明△AGD≌△DCE即可得到结论.【详解】证明：过D作DG∥AC交AB于G，∵△ABC是等边三角形，∴AB＝AC，∠B＝∠ACB＝∠BAC＝60°，又∵DG∥AC，∴∠BDG＝∠BGD＝60°，∴△BDG是等边三角形，∠AGD＝180°−∠BGD＝120°，∴DG＝BD，∵点D为BC的中点，∴BD＝CD，∴DG＝CD，∵EC是△ABC外角的平分线，∴∠ACE＝（180°−∠ACB）＝60°，∴∠BCE＝∠ACB＋∠ACE＝120°＝∠AGD，∵AB＝AC，点D为BC的中点，∴∠ADB＝∠ADC＝90°，又∵∠BDG＝60°，∠ADE＝60°，∴∠ADG＝∠EDC＝30°，在△AGD和△ECD中，，∴△AGD≌△ECD（ASA）．∴AD＝DE．【点睛】本题是三角形综合题，主要考查了平行线的性质，全等三角形的性质与判定，等边三角形的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键．7、见解析【分析】由，得出为等腰三角形，由外角的性质及等量代换得，再次利用外角的性质及等量代换得，即可证明．【详解】解：，为等腰三角形，，由外角的性质得：，，再由外角的性质得：，，．【点睛】本题考查了等腰三角形、外角的性质、解题的关键是掌握外角的性质及等量代换的思想进行求解．8、（1）见解析（2）的面积为20．【分析】（1）根据已知条件得到、，然后利用全等三角形的判定，进行证明即可．（2）分别根据和的面积，用CF表示AF、DF，通过，得到，，用CF表示出AE的长，最后利用面积公式求解即可．（1）（1）解：由题意可知： 是的中线 在与中 ．（2）解：的面积为8，的面积为6．，即 ，即 由（1）可知：， ．【点睛】本题主要是考查了全等三角形的判定和性质，熟练根据条件证明三角形全等，利用其性质，证明对应边相等，这是解决本题的关键．9、【分析】先由旋转的性质证明再利用等边对等角证明从而可得答案.【详解】解： 把△ABC绕点A逆时针旋转得到△ADE，∠B＝70°， 【点睛】本题考查的是旋转的性质，等腰三角形的性质，掌握“旋转前后的对应角相等与等边对等角”是解本题的关键.10、（1）见解析；（2）见解析．【分析】（1）以点D为圆心，适当长为半径，作弧，交AC于两点，再分别以这两点为圆心，适当长为半径作弧，连接两条弧的交点所在的直线，该直线与AC的交点即为点F，连接交于点；（2）利用角平分线性质可得，由此证明，得到，继而证明，证得即可解题．【详解】解：（1）如图，点F、G即为所求作的点；（2）是的角平分线，，，【点睛】本题考查角平分线的性质、全等三角形的判定与性质等知识，是重要考点，难度一般，掌握相关知识是解题关键．