还剩6页未读，
继续阅读
北师大版七年级下册3 探索三角形全等的条件习题课件ppt
展开
这是一份北师大版七年级下册3 探索三角形全等的条件习题课件ppt，共11页。PPT课件主要包含了答案呈现等内容，欢迎下载使用。
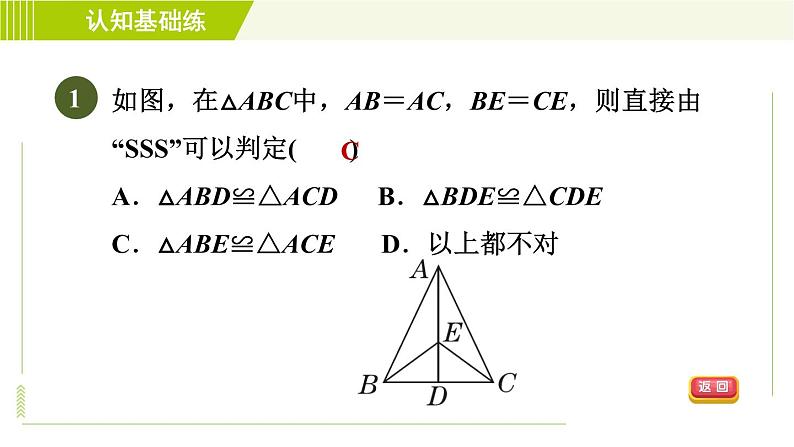
如图，在△ABC中，AB＝AC，BE＝CE，则直接由“SSS”可以判定( )A．△ABD≌△ACD B．△BDE≌△CDEC．△ABE≌△ACE D．以上都不对
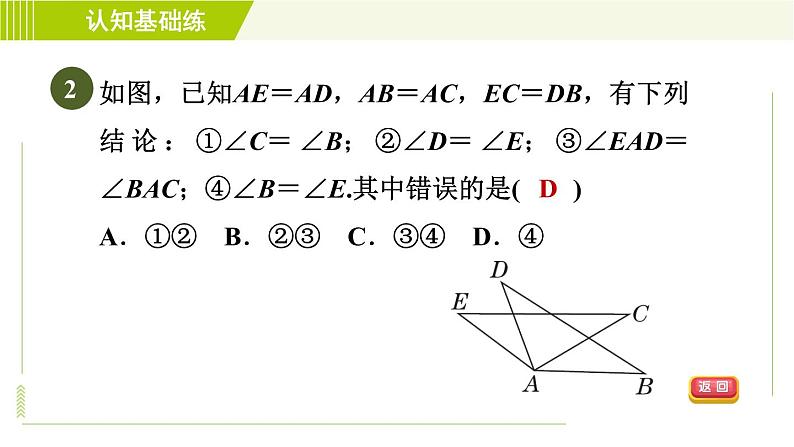
如图，已知AE＝AD，AB＝AC，EC＝DB，有下列结论：①∠C＝∠B；②∠D＝∠E；③∠EAD＝∠BAC；④∠B＝∠E.其中错误的是( )A．①② B．②③ C．③④ D．④
【2021·云南】如图，在四边形ABCD中，AD＝BC，AC＝BD，AC与BD相交于点E.试说明：∠DAC＝∠CBD.
如图，已知AB＝AC，AE＝AD，点B，D，E，C在同一条直线上，要利用“SSS”推理得出△ABE≌△ACD，还需要添加的一个条件可以是( )A．BD＝DE B．BD＝CEC．DE＝CE D．以上都不对
如图，已知线段AB，CD相交于点O，AD，CB的延长线交于点E，OA＝OC，EA＝EC. (1)试说明∠A＝∠C；
(2)在(1)的解答过程中，需要作辅助线，它的意图是什么？
本题运用了构造法，通过连接OE，构造△OAE和△OCE，将欲说明相等的∠A，∠C分别置于这两个三角形中，然后通过说明这两个三角形全等可得∠A＝∠C.
如图，在△ABC中，AC＝BC，D是AB上的一点，AE⊥CD于点E，BF⊥CD于点F.若CE＝BF，AE＝EF＋BF，试判断AC与BC的位置关系，并说明理由．
解：AC⊥BC.理由如下：因为CE＝BF，AE＝EF＋BF，CF＝CE＋EF，所以AE＝CF.
如图，在△ABC中，AB＝AC，BE＝CE，则直接由“SSS”可以判定( )A．△ABD≌△ACD B．△BDE≌△CDEC．△ABE≌△ACE D．以上都不对
如图，已知AE＝AD，AB＝AC，EC＝DB，有下列结论：①∠C＝∠B；②∠D＝∠E；③∠EAD＝∠BAC；④∠B＝∠E.其中错误的是( )A．①② B．②③ C．③④ D．④
【2021·云南】如图，在四边形ABCD中，AD＝BC，AC＝BD，AC与BD相交于点E.试说明：∠DAC＝∠CBD.
如图，已知AB＝AC，AE＝AD，点B，D，E，C在同一条直线上，要利用“SSS”推理得出△ABE≌△ACD，还需要添加的一个条件可以是( )A．BD＝DE B．BD＝CEC．DE＝CE D．以上都不对
如图，已知线段AB，CD相交于点O，AD，CB的延长线交于点E，OA＝OC，EA＝EC. (1)试说明∠A＝∠C；
(2)在(1)的解答过程中，需要作辅助线，它的意图是什么？
本题运用了构造法，通过连接OE，构造△OAE和△OCE，将欲说明相等的∠A，∠C分别置于这两个三角形中，然后通过说明这两个三角形全等可得∠A＝∠C.
如图，在△ABC中，AC＝BC，D是AB上的一点，AE⊥CD于点E，BF⊥CD于点F.若CE＝BF，AE＝EF＋BF，试判断AC与BC的位置关系，并说明理由．
解：AC⊥BC.理由如下：因为CE＝BF，AE＝EF＋BF，CF＝CE＋EF，所以AE＝CF.
相关课件
北师大版七年级下册第四章 三角形3 探索三角形全等的条件获奖备课ppt课件： 这是一份北师大版七年级下册<a href="/sx/tb_c9990_t3/?tag_id=26" target="_blank">第四章 三角形3 探索三角形全等的条件获奖备课ppt课件</a>，文件包含431《利用“边边边”判定三角形全等》课件pptx、431《利用“边边边”判定三角形全等》教案doc、431《利用“边边边”判定三角形全等》练习doc、431《利用“边边边”判定三角形全等》学案doc等4份课件配套教学资源，其中PPT共30页， 欢迎下载使用。
北师大版七年级下册3 探索三角形全等的条件习题ppt课件： 这是一份北师大版七年级下册3 探索三角形全等的条件习题ppt课件，文件包含43第1课时边边边ppt、43-1ppt、43第1课时利用“边边边”判定三角形全等docx、sss431wmv等4份课件配套教学资源，其中PPT共36页， 欢迎下载使用。
初中数学北师大版七年级下册3 探索三角形全等的条件授课ppt课件： 这是一份初中数学北师大版七年级下册3 探索三角形全等的条件授课ppt课件，共20页。PPT课件主要包含了学习目标，①已知一条边，②已知一个角，①已知两条边，②已知两个角，③已知一条边和一个角，①已知三个角，②已知三条边，③已知两角一边，④已知两边一角等内容，欢迎下载使用。
