数学八年级上册15.4 角的平分线课前预习ppt课件

这是一份数学八年级上册15.4 角的平分线课前预习ppt课件，共15页。PPT课件主要包含了探究新知，探究角平分线的性质，实践应用等内容，欢迎下载使用。

不利用工具，请你将一张用纸片做的角分成两个相等的角。你有什么办法？
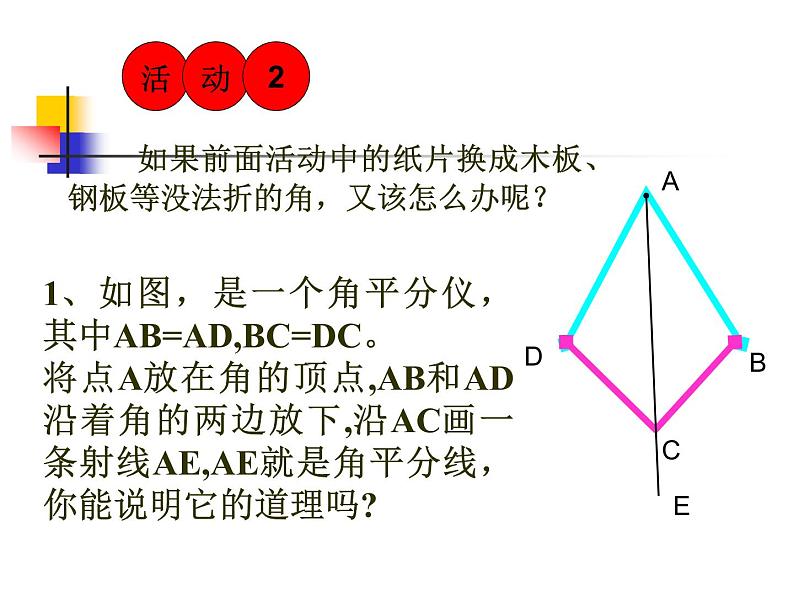
1、如图，是一个角平分仪，其中AB=AD,BC=DC。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线，你能说明它的道理吗?
如果前面活动中的纸片换成木板、钢板等没法折的角，又该怎么办呢？
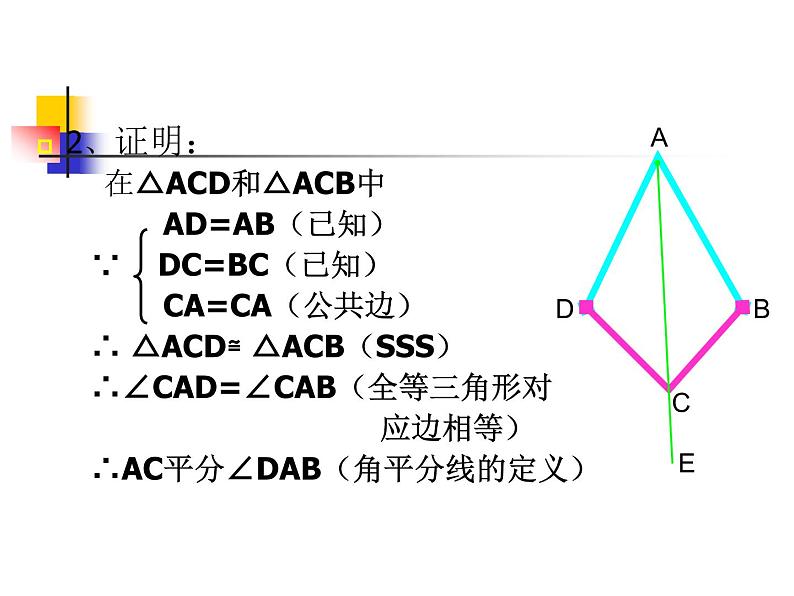
2、证明： 在△ACD和△ACB中 AD=AB（已知） ∵ DC=BC（已知） CA=CA（公共边） ∴ △ACD≌ △ACB（SSS） ∴∠CAD=∠CAB（全等三角形对 应边相等） ∴AC平分∠DAB（角平分线的定义）
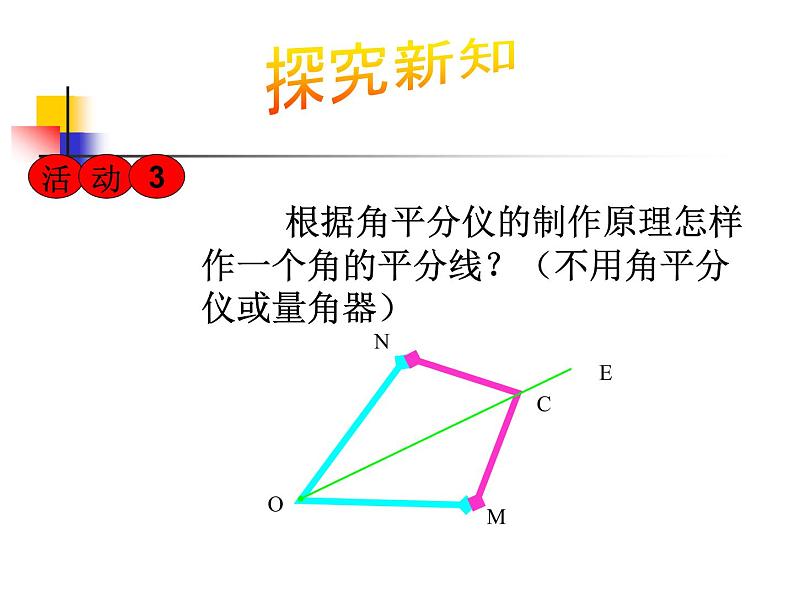
根据角平分仪的制作原理怎样作一个角的平分线？（不用角平分仪或量角器）
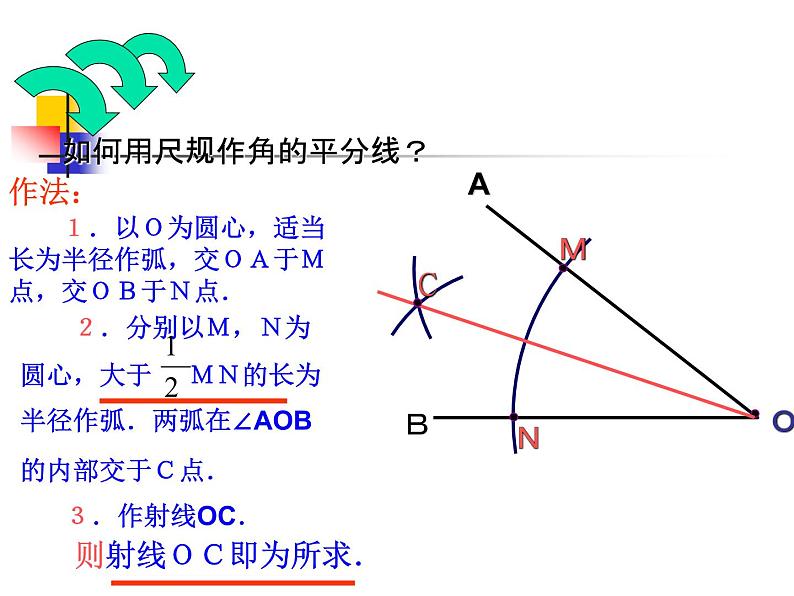
如何用尺规作角的平分线？
　　１．以Ｏ为圆心，适当长为半径作弧，交ＯＡ于Ｍ点，交ＯＢ于Ｎ点．
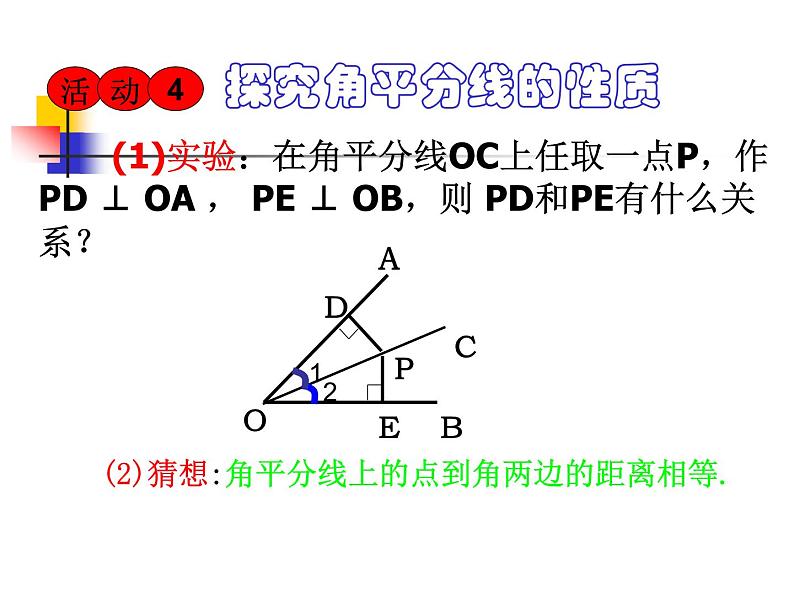
(1)实验：在角平分线OC上任取一点P，作PD ⊥ OA ， PE ⊥ OB，则 PD和PE有什么关系？
(2)猜想:角平分线上的点到角两边的距离相等.
证明：∵OC平分∠ AOB （已知） ∴ ∠1= ∠2（角平分线的定义） ∵PD ⊥ OA，PE ⊥ OB（已知） ∴ ∠PDO= ∠PEO=90°（垂直的定义） 在△PDO和△PEO中 ∠PDO= ∠PEO（已证） ∵ ∠1= ∠2 （已证） OP=OP （公共边） ∴ △PDO ≌ △PEO（AAS） ∴PD=PE（全等三角形的对应边相等）
已知：如图，OC平分∠AOB，点P在OC上，PD⊥OA于点D，PE⊥OB于点E求证: PD=PE
角平分线上的点到角两边的距离相等。
(4)得到角平分线的性质：
利用此性质怎样书写推理过程?(几何语言)
如图：在△ABC中，∠C=90° AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF； 求证：CF=EB
从这节课中你有哪些收获？
1：画一个已知角的角平分线；(注意作图痕迹和几何语言的表达)
3：角平分线性质定理的应用．
2：角平分线的性质： 角平分线上的点到角两边的距离相等．
1.如图,在△ABC中，AC⊥BC，AD为∠BAC的平分线，DE⊥AB，AB＝7㎝，AC＝3㎝，求BE的长。
2.在Rt△ABC中，BD平分∠ABC， DE⊥AB于E，则：⑴图中相等的线段有哪些？相等的角呢？⑵哪条线段与DE相等？为什么？⑶若AB＝10，BC＝8，AC＝6，　　　　　　求BE，AE的长和△AED的周长。