初中数学华师大版八年级上册第14章 勾股定理综合与测试复习ppt课件

这是一份初中数学华师大版八年级上册第14章 勾股定理综合与测试复习ppt课件，共12页。PPT课件主要包含了AB是圆柱的高，AC≈1077cm，L1AC，L2AB+BC，解法如下，L12AC2，AB2+BC2，h2+πr2，h+2r2等内容，欢迎下载使用。
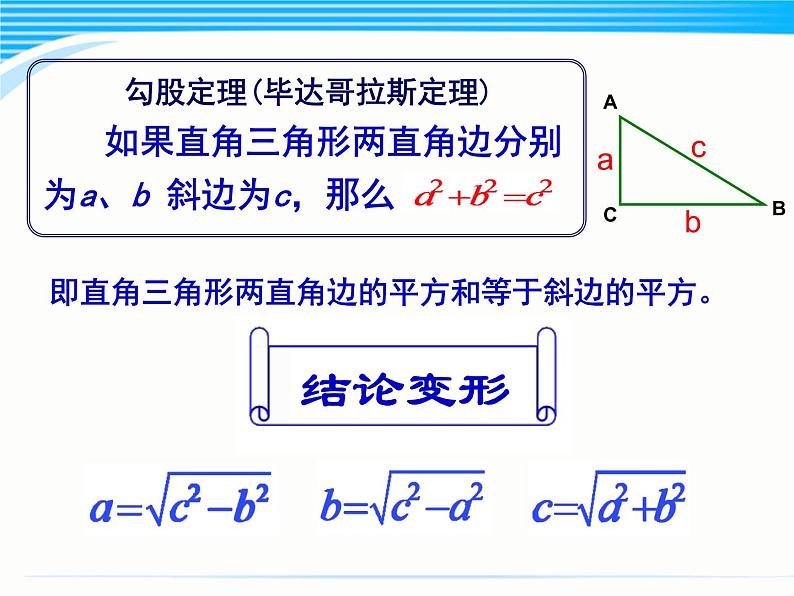
即直角三角形两直角边的平方和等于斜边的平方。
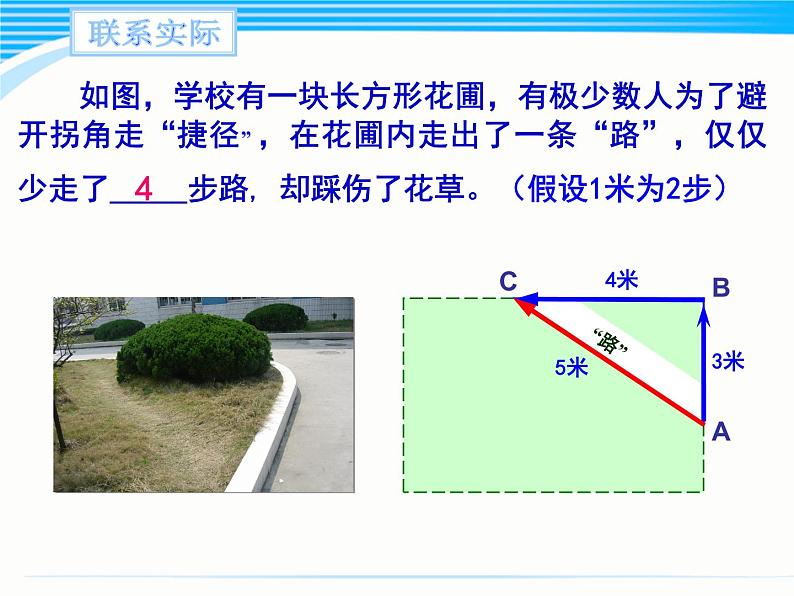
如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径” ，在花圃内走出了一条“路”，仅仅少走了_____步路, 却踩伤了花草。（假设1米为2步）
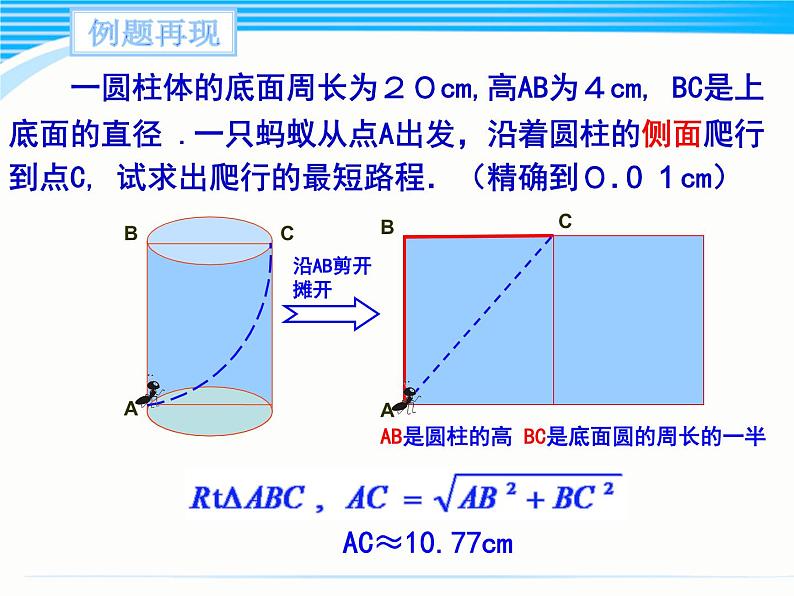
一圆柱体的底面周长为２０cm,高AB为４cm, BC是上底面的直径 .一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C, 试求出爬行的最短路程．（精确到０.０１cm）
BC是底面圆的周长的一半
如图（1），一圆柱的底面半径为5，BC是底面直径，圆柱高AB为5，求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线。小明设计了两条路线：路线1：侧面展开图中的线段AC.如图（２）所示. 用L1表示设路线1的长度为L1 ,则L12= AC2 =AB2+BC2 =52+（5π）2 =25+25π2路线2：高线AB+底面直径BC.如图(1)所示.用L2表示
设路线2的长度为L2,则L22 = (AB+BC)2 =（5+10）2=225
∵ L12－L22=25+25π2－225=25(π2－8)＞0
∴ L12＞L22. ∴ L1＞L2
所以选择路线L2较短.
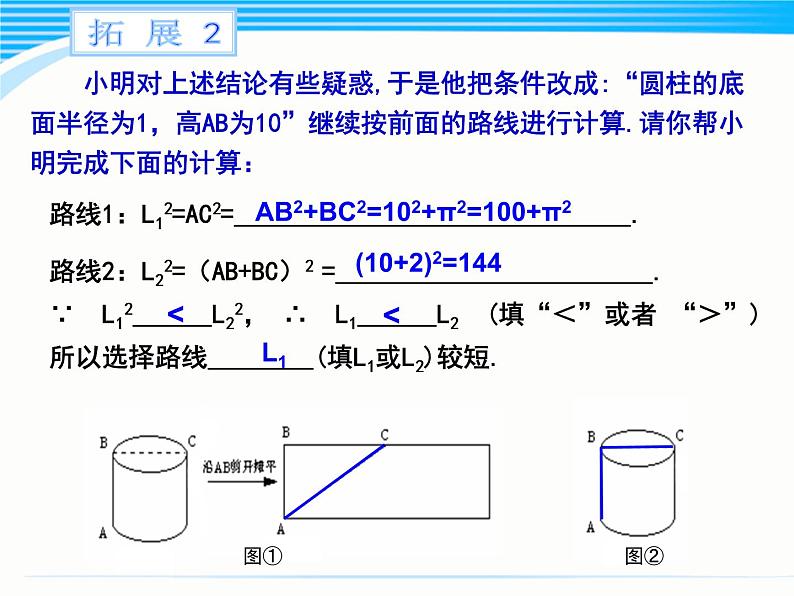
小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1，高AB为10”继续按前面的路线进行计算.请你帮小明完成下面的计算：
路线1：L12=AC2= .路线2：L22=（AB+BC）2 = . ∵ L12 L22， ∴ L1 L2 (填“＜”或者 “＞”) 所以选择路线 (填L1或L2)较短.
AB2+BC2=102+π2=100+π2
(10+2)2=144
请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r和高为h满足什么条件时，应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短.（分组讨论，看哪组最快得到答案）
L22=(AB+BC)2=
L12-L22=h2+(πr)2 －(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h ]
∵L1 ＞0,L2 ＞0
∴L1和L2的大小，与L12 和L22的大小关系一样，又∵r＞0, π2－4＞0
∴当r= 时，L12 = L22 ,L1= L2，选择路线L1, L2都一样；
当r> 时，L12 >L22 ,L1＞ L2，选择路线L2较短；
当r< 时，L12< L22 ,L1＜ L2 ，选择路线L1较短。
图①所示的正方体木块棱长为6cm，沿其相邻三个面的对角线（图中虚线）剪掉一角，得到如图②的几何体，一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为 cm．
如图长为3cm，宽为2cm，高为1cm的长方体，蚂蚁沿着表面从点A到点B需要爬行的最短路程是多少？
本节课主要学习了勾股定理的应用——立体图形中最短路径问题，其一般解题思路如下： 1、展：立体图形 → 平面图形；2、找：最短路线 起点→终点 依据是平面内两点之间线段最短；3、算：构造出直角三角形，从而利用勾股定理进行计算。