





初中数学人教版八年级下册17.1 勾股定理教学ppt课件
展开1.运用勾股定理解决实际问题 ;(重点)2.勾股定理的灵活运用 .(难点)
如果直角三角形两直角边分别为a , b , 斜边为c , 那么
即 直角三角形两直角边的平方和等于斜边的平方 .
1. 已知Rt△ABC中 , ∠C=90° , 若 a=1 , c=3 , 则 b= .
2. 已知Rt△ABC中 , ∠A=90° , ∠B=30° , 若 a=4 , 则 c= . Zx```x``k
3. 已知Rt△ABC中 , ∠B=90° , ∠A=45° , 若 b=7 , 则 c= .
电视的尺寸是屏幕对角线的长度 . 小华的爸爸买了一台29英寸 (74cm) 的电视机 , 小华量电视机的屏幕后 , 发现屏幕只有58cm 长和 46cm 宽 . 他觉得一定是售货员搞错了 , 你同意他的想法吗 ? 你能解释是为什么吗 ?
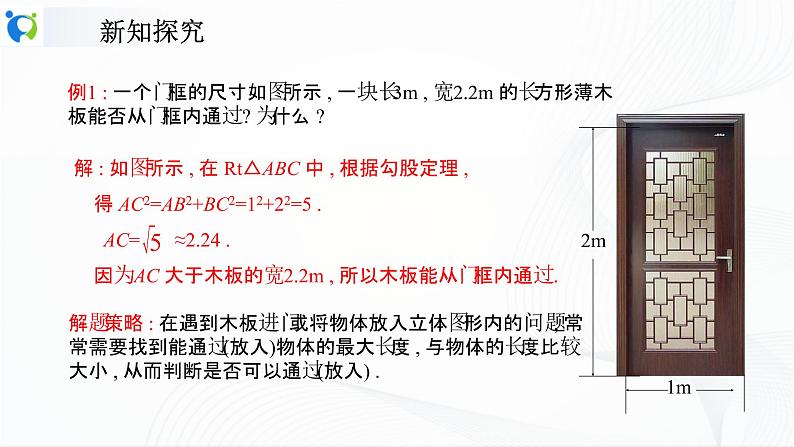
例1 : 一个门框的尺寸如图所示 , 一块长 3m , 宽 2.2m 的长方形薄木板能否从门框内通过 ? 为什么 ?
解 : 如图所示 , 在 Rt△ABC 中 , 根据勾股定理 , 得 AC2=AB2+BC2=12+22=5 . AC= ≈2.24 . 因为 AC 大于木板的宽 2.2m , 所以木板能从门框内通过 .
解题策略 : 在遇到木板进门或将物体放入立体图形内的问题, 常常需要找到能通过(放入)物体的最大长度 , 与物体的长度比较大小 , 从而判断是否可以通过(放入) .
例2 : 如图所示 , 一架 2.6m 长的梯子 AB 斜靠在一竖直的墙 AO 上 , 这时 AO 为2.4m . 如果梯子的顶端 A 沿墙下滑 0.5m , 那么梯子底端 B 也外移 0.5m 吗 ?
解:可以看出 , BD=OD-OB . 在 Rt△AOB 中 , 根据勾股定理 , 得 OB2=AB2-OA2=2.62-2.42=1 , OB= =1 . 在 Rt△COD 中, 根据勾股定理 , 得 OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15 , OD= ≈1.77. BD=OD-OB≈1.77-1=0.77 . 所以梯子的顶端沿墙下滑 0.5m 时 , 梯子底端并不是 也外移 0.5m , 而是外移约 0.77m .
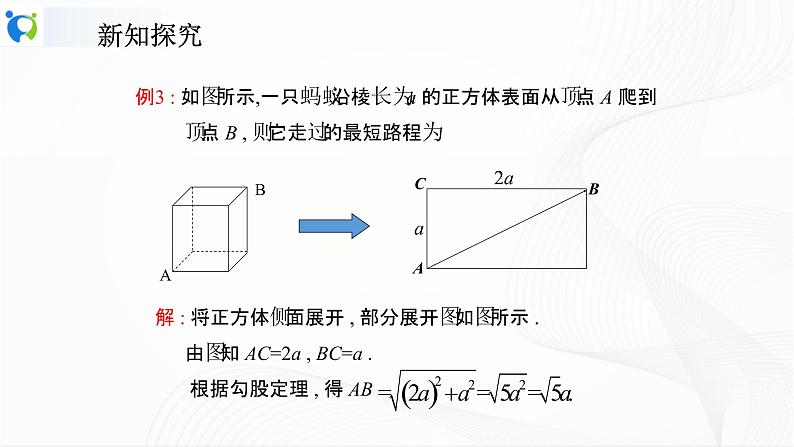
例3 : 如图所示,一只蚂蚁沿棱长为 a 的正方体表面从顶点 A 爬到 顶点 B , 则它走过的最短路程为
解 : 将正方体侧面展开 , 部分展开图如图所示 . 由图知 AC=2a , BC=a . 根据勾股定理 , 得 AB
勾股定理应用的条件必须是直角三角形 , 所以要应用勾股定理必须构造直角三角形 . 常见的应用类型为 : ① 化非直角三角形为直角三角形 ;② 将实际问题转化为直角三角形模型 .
1.一辆装满货物的卡车 , 其外形高 2.5米 , 宽 1.6米 , 要开进厂门形状如图的某工 厂 , 问这辆卡车能否通过该工厂的厂 门 ? 说明理由 .
当车的高度﹥CH 时 , 则车 通过 ;当车的高度﹤CH 时 , 则车 通过 .
由图可知:CH =DH+CD , OD=0.8米 , OC= 1米 , CD⊥AB, 于是车能否通过这个问题就转化到直角△ODC中CD这条边上 ;
解 : 由于厂门宽度足够 , 所以卡车能否通过 , 只要看当卡车位于厂门正中间时其高度与 CH 值的大小比较 .
根据勾股定理得 : CD= = =0.6(米) 2.3+0.6=2.9﹥2.5 , ∴卡车能通过 .
CH的值是多少 , 如何计算呢 ?
2.我国古代数学著作《九章算术》中的一个问题 , 原文是 : 今有方池一丈 , 葭生其中央 , 出水一尺 , 引葭赴岸 , 适 与岸齐 , 水深 , 葭长各几何 ? 请用学过的数学知识回答 这个问题 .
译 : 有一个水池 , 水面是一个为10尺的正方形 , 在水池正中央有一根芦苇 , 它高出水面一尺 . 如果把这根芦苇拉向水池一边的中点 , 它的顶端恰好到达池边的水面 . 这个水池的深度与这根芦苇的长度分别是多少 ?
解:设水池的深度AC为x米 , 则芦苇高AD为 (x+1)米 .
根据题意得:BC2+AC2=AB2,
∴52+x2 =(x+1)2
25+x2=x2+2x+1
∴x+1=12+1=13(米) .
答:水池的深度为12米 , 芦苇高为13米 .
用勾股定理计算时 , 要先画好图形 , 并标好图形 , 理清各边之间的关系 , 再灵活运用勾股定理计算
在利用勾股定理进行有关计算和证明时 ,要注意运用方程的思想 ; 求直角三角形有关线段的长 , 有时还要运用转化的数学思想 , 或利用添加辅助线的方法构造直角三角形 , 再运用勾股定理求解
1.小明用火柴棒摆直角三角形 , 已知他摆两条直角边分别用了6 根和 8 根火柴棒 , 他摆完这个直角三角形共用火柴棒 ( ) A.20根 B.14根 C.24根 D.30根
2.如图 , △ABC中∠C=90° , AD平分∠BAC , DE⊥AB于E , 下面等式错误的是( )
3.为迎接新年的到来 , 同学们做了许多花布置教室 , 准备召开新年晚会 . 小刘搬来一架高 2.5 米的木梯 , 木梯放好后 , 顶端与地面的距离为 2.4米 , 则梯脚与墙脚的距离应为 ( ) A.0.7米 B.0.8米 C.0.9米 D.1.0米
4.我国古代有这样一道数学问题 :“枯木一根直立地上 , 高二丈 , 周三尺 , 有葛藤自根缠绕而上 , 五周而达其顶 , 问葛藤之长几何 ?” 题意是 : 如图所示 , 把枯木看作一个圆柱体 , 因一丈是十尺 , 则该圆柱的高为20尺 , 底面周长为3尺 , 有葛藤自点A处缠绕而上 , 绕五周后其末端恰好到达点B处 . 则问题中葛藤的最短长度是 尺 .
5.如图 , 山坡的坡角为30° , 山坡上两株木之间的坡面距离是 米 , 则这两株树之间的垂直距离是 米 , 水平距离是 米 .
6.如图所示 , 两点 A , B 都与平面镜 CD 相距 4米 , 且 A , B 两点相距 6米 , 一束光由 A 点射向平面镜 , 反射之后恰好经过 B 点 , 求 B 点与入射点间的距离 .
解:作出B点关于CD的对称点B' , 连接AB' , 交CD于点O, 则O点就是光的入射点 , 连接OB , 因为 AC=BD , ∠ACO=∠BDO=90°, ∠AOC=∠BOD , 所以 △AOC≌△BOD . 所以 OC=OD= AB=3米 . 在 Rt△ODB中 , OD2+BD2=OB2 , 所以 OB2=32+42=25 , 所以OB=5米 .
7.如图 , 铁路上A , B两点相距25km , C , D为两庄 , DA⊥AB于A , CB⊥AB于B , 已知 DA=15km , CB=10km , 现在要在铁路AB上建一个土特产品收购站E , 使得C , D两村到E站的距离相等 , 则E站应建在离A站多少千米处 ?
解:设AE= x km ,
根据勾股定理 , 得 AD2+AE2=DE2 , BC2+BE2=CE2 ,
又 ∵ DE=CE ,
∴ AD2+AE2= BC2+BE2 .
即:152+x2=102+(25-x)2
答:E站应建在离A站10 km处 .
则 BE=(25-x) km ,
初中数学人教版八年级下册17.1 勾股定理优秀ppt课件: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10261_t3/?tag_id=26" target="_blank">17.1 勾股定理优秀ppt课件</a>,文件包含1712《勾股定理的应用》课件pptx、1712《勾股定理的应用》教案docx、1712《勾股定理的应用》分层作业原卷版docx、1712《勾股定理的应用》分层作业解析版docx等4份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
人教版八年级下册17.1 勾股定理教课课件ppt: 这是一份人教版八年级下册17.1 勾股定理教课课件ppt,文件包含第2课时勾股定理的应用pptx、勾股定理的应用mp4等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
人教版八年级下册17.1 勾股定理精品课件ppt: 这是一份人教版八年级下册17.1 勾股定理精品课件ppt,共17页。PPT课件主要包含了复习回顾,问题1,几何语言,新知探究,探究一,问题2,木板可以斜着过吗,探究二,∴OB1,≈57m等内容,欢迎下载使用。













