初中数学北师大版七年级下册2 探索轴对称的性质习题课件ppt

这是一份初中数学北师大版七年级下册2 探索轴对称的性质习题课件ppt，共20页。PPT课件主要包含了答案显示，垂直平分相等相等，特殊点对称点顺次，见习题，垂直平分，2求∠F的度数，特殊点，对称点等内容，欢迎下载使用。

1．在轴对称图形或两个成轴对称的图形中，对应点所连的线段被对称轴__________，对应线段________，对应角________．
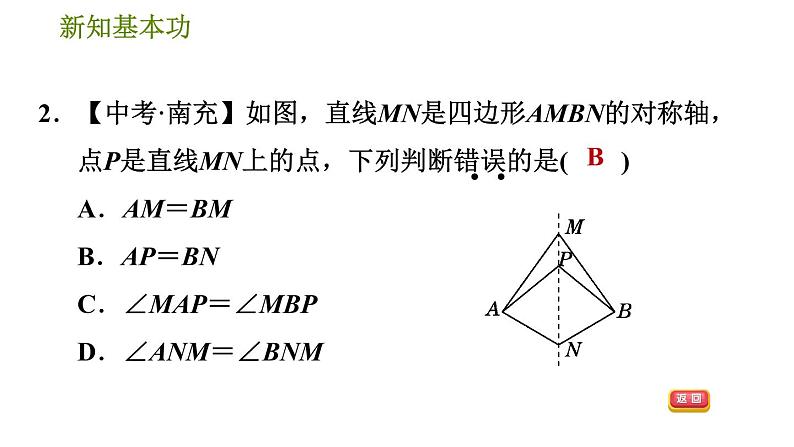
2．【中考·南充】如图，直线MN是四边形AMBN的对称轴，点P是直线MN上的点，下列判断错误的是(　　)A．AM＝BM B．AP＝BNC．∠MAP＝∠MBP D．∠ANM＝∠BNM
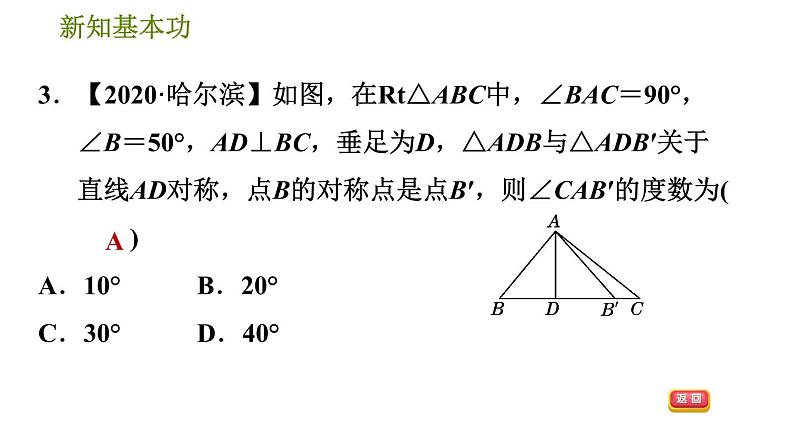
3．【2020·哈尔滨】如图，在Rt△ABC中，∠BAC＝90°，∠B＝50°，AD⊥BC，垂足为D，△ADB与△ADB′关于直线AD对称，点B的对称点是点B′，则∠CAB′的度数为(　　)A．10° B．20° C．30° D．40°
4．【教材P118做一做变式】如图，△ABC与△DEF关于直线MN对称，其中∠C＝90°，AC＝8 cm，DE＝10 cm，BC＝6 cm.(1)线段AD与MN的关系是什么？
解：因为△ABC与△DEF关于直线MN对称，所以MN垂直平分AD.
解：因为△ABC与△DEF关于直线MN对称，所以∠F＝∠C＝90°.
(3)求△ABC的周长和△DEF的面积．
5．利用特殊点画对称图形的步骤：先确定图形中的________，再分别画出这些特殊点的________，最后按原图形中的方式________连接各对称点．
6．下面是四名同学作△ABC关于直线MN对称的△A′B′C′，其中正确的是(　　)
7．【教材P120习题T3变式】如图所示的两个轴对称图形分别只画了一半，请画出它们的另一半(直线l为对称轴)．
8．如图，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC(即三角形的顶点都在格点上)．(1)在图中画出△ABC关于直线l对称的△A1B1C1(要求：点A与A1，B与B1，C与C1相对应)；
(2)在(1)的条件下，连接AA1，CC1，求四边形AA1C1C的面积．
9．【2021·常州】如图，B，F，C，E是直线l上的四点，AB∥DE，AB＝DE，BF＝CE.(1)试说明：△ABC≌△DEF；
(2)将△ABC沿直线l翻折得到△A′BC.①用直尺和圆规在图中作出△A′BC(保留作图痕迹，不要求写作法)；②连接A′D，则直线A′D与l的位置关系是________．
解：如图所示，△A′BC即为所求．
解：因为M，N分别是点P关于AO，BO的对称点，所以ME＝PE，NF＝PF.又因为△PEF的周长为20 cm，所以PE＋EF＋PF＝20 cm.所以ME＋EF＋FN＝20 cm，即MN＝20 cm.
10．如图，点P在∠AOB内，M，N分别是点P关于AO，BO的对称点，MN分别交AO，BO于点E，F.若△PEF的周长等于20 cm，求MN的长．
11．【2020·吉林】图①、图②、图③都是3×3的正方形网格，每个小正方形的顶点称为格点．A，B，C均为格点，在给定的网格中，按下列要求画图．(1)在图①中，画一条不与AB重合的线段MN，使MN与AB关于某条直线对称，且M，N为格点；
解：如图①，MN即为所求．(答案不唯一)
(2)在图②中，画一条不与AC重合的线段PQ，使PQ与AC关于某条直线对称，且P，Q为格点；
(3)在图③中，画一个△DEF，使△DEF与△ABC关于某条直线对称，且D，E，F为格点．
解：如图②，PQ即为所求．(答案不唯一)
如图③，△DEF即为所求．(答案不唯一)