人教A版 (2019)必修 第一册4.4 对数函数一等奖教学ppt课件

这是一份人教A版 (2019)必修 第一册4.4 对数函数一等奖教学ppt课件，共22页。PPT课件主要包含了学习目标，新知学习，随堂小测，log2x，－∞0，课堂小结等内容，欢迎下载使用。

1.了解对数函数的概念，体会对数函数是一类重要的函数模型.2.能用描点法或借助计算工具画出具体对数函数的图象，探索并了解对数函数的单调性与特殊点.3.知道指数函数y＝ax与对数函数y＝lgax（a>0，且a≠1）互为反函数.4.比较几类函数模型增长的差异，并利用函数模型解决简单的实际问题.核心素养：数学抽象、数学 建模、直观想象
【定义】根据指数与对数的关系，由 可以得到
也是 的函数.而通常我们用 表示自变量，用
一般地，函数 叫做对数函数，其中 是自变量，定义域是(0，+∞)
【问题】怎样判断一个函数是不是对数函数？
【答】抓住对数函数解析式的三个结构特征：
【1】 的系数为1
【2】 底数 满足 .
【3】 真数是自变量 .
为什么对数函数的定义域是(0，+∞)？
【答】由函数定义及解析式 可知，对数函数的自 变量 恰好是指数 函数的函数值 ， 所以对数函数的定义 域是(0，+∞)
【1】求下列函数的定义域.
所以函数 的定义域是
所以函数 的定义域是
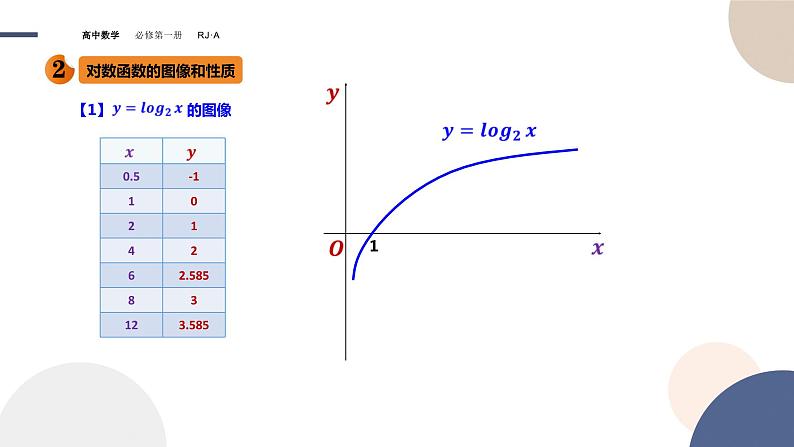
【1】 的图像
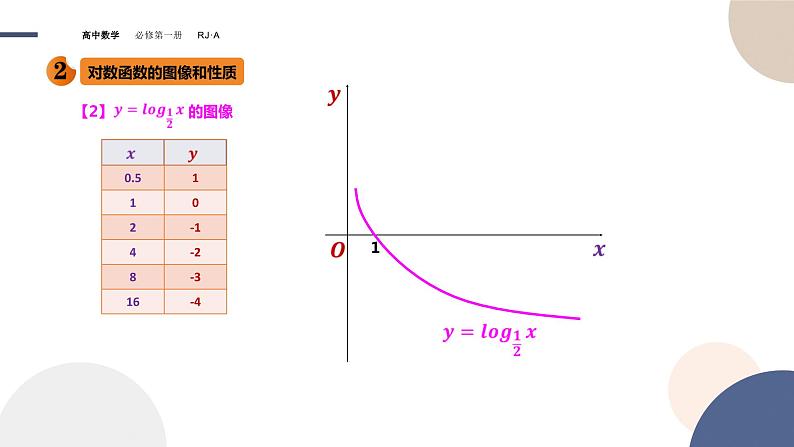
【2】 的图像
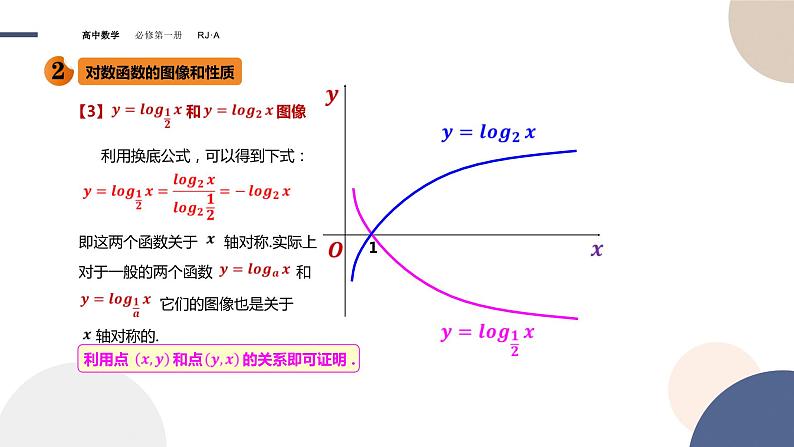
【3】 和 图像
利用换底公式，可以得到下式：
即这两个函数关于 轴对称.实际上
对于一般的两个函数 和
利用点 和点 的关系即可证明 .
在同一坐标系中画出不同底数的图像，通过图像我们发现除了 和 的图像关于 轴对称之外，还可以把底数 分成和 两种情况来讨论:
【问题】怎样画出对数函数的图像？
三个点之后，用平滑的曲线连接起来即可.
①图像都在y轴右侧②都经过点（1，0）③无限靠近y轴但不相交④ 时，图像上升⑤ 时，图像下降
【注意】①对数函数值的变化：
②对数函数单调性口诀：
对数函数有两种，底数大小要分清；
底数若是大于1，图像从左往右增.
底数0到1之间1，图像从左往右减；
无论函数增或减，图像都过(1,0)点.
【1】比较下列各式的大小.
【探究】观察图像可以发现，指数函数 ，定义域R,值域(0,+∞)和对数函数 ，定义域为(0,+∞)，值域为R，他们的定义域和值域恰好相 反，并且它们的图像关于直线 对称，那么我们就称函数 的反函数是 ，函数 的反函数是 这两个函数互为反函数.
【结论】一般地，指数函数 与对数函数 互为反函数，它们的定义域和值域互换.
【指数函数和对数函数的比较】
两个函数互为反函数，图像关于直线对称
【1】求下面函数的定义域.
1.下列函数为对数函数的是A.y＝lgax＋1(a＞0且a≠1)B.y＝lga(2x)(a＞0且a≠1)C.y＝lg(a－1)x(a＞1且a≠2)D.y＝2lgax(a＞0且a≠1)
2.函数y＝lg2(x－2)的定义域是A.(0，＋∞) B.(1，＋∞)C.(2，＋∞) D.[4，＋∞)
3.函数y＝2lg4(1－x)的图象大致是
解析　函数y＝2lg4(1－x)的定义域为(－∞，1)，排除A，B；又函数y＝2lg4(1－x)在定义域内单调递减，排除D.故选C.
4.若函数y＝f(x)是函数y＝ax(a>0，且a≠1)的反函数，且f(2)＝1，则f(x)＝_____.
5.函数f(x)＝ln x2的减区间为_________.
1.含有对数符号“lg”的函数不一定是对数函数.判断一个函数是否为对数函数，不仅要含有对数符号“lg”，还要符合对数函数的概念，即形如y＝lgax(a>0，且a≠1)的形式.如：y＝2lg2x，y＝lg5 都不是对数函数，可称其为对数型函数.2.研究y＝lgaf(x)的性质如定义域、值域、比较大小，均需依托对数函数的相应性质.3.研究与对数函数图象有关的问题，以对数函数图象为基础，加以平移、伸缩、对称或截取一部分.
4.与对数函数有关的复合函数的单调区间、奇偶性、不等式问题都要注意定义域的影响.5.y＝ax与x＝lgay图象是相同的，只是为了适应习惯用x表示自变量，y表示因变量，把x＝lgay换成y＝lgax，y＝lgax才与y＝ax关于y＝x对称，因为(a，b)与(b，a)关于y＝x对称.