人教版数学七年级上册精品教学课件第四章几何图形初步小结课时2-数学人教七（上）

这是一份人教版数学七年级上册精品教学课件第四章几何图形初步小结课时2-数学人教七（上），共25页。
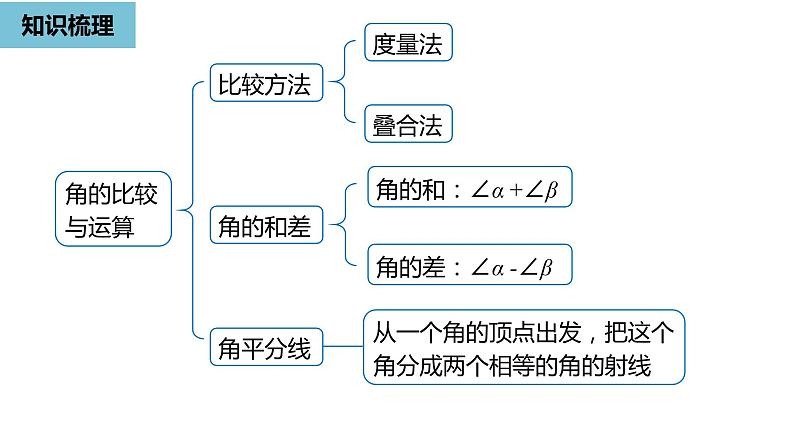
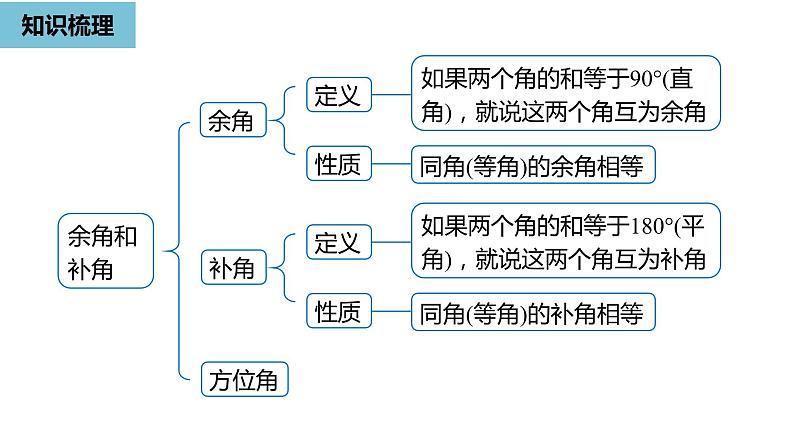
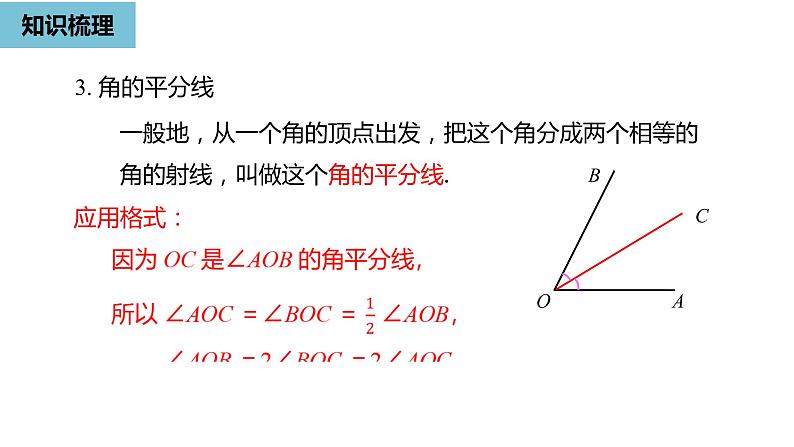
小结几何图形初步人教版-数学-七年级上册知识梳理-重点解析-深化练习知识梳理表示方法角三个大写字母一个大写字母一个数字一个小写希腊字母度量单位：度、分、秒1°=60′，1′=60″概念有公共端点的两条射线组成的图形由一条射线绕着它的端点旋转而形成的图形知识梳理从一个角的顶点出发，把这个角分成两个相等的角的射线角的比较与运算角的和：∠α +∠β比较方法度量法叠合法角的和差角的差：∠α -∠β角平分线知识梳理余角如果两个角的和等于90°(直角)，就说这两个角互为余角余角和补角定义性质同角(等角)的余角相等方位角补角如果两个角的和等于180°(平角)，就说这两个角互为补角定义性质同角(等角)的补角相等知识梳理1. 角的定义(1) 有公共端点的两条射线组成的图形，叫做角.(2) 角也可以看作由一条射线绕着它的端点旋转而形成的图形.2. 角的度量度、分、秒的互化1°＝60′，1′＝60″知识梳理3. 角的平分线一般地，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线. 应用格式：OBAC 知识梳理4. 余角和补角(1) 定义① 如果两个角的和等于90°( 直角 )，就说这两个角互为余角 ( 简称为两个角互余 ).② 如果两个角的和等于180°(平角)，就说这两个角互为补角 ( 简称为两个角互补 ).(2) 性质 ① 同角 (等角) 的余角相等. ② 同角 (等角) 的补角相等.知识梳理(3) 方位角① 定义物体运动的方向与正北、正南方向之间的夹角称为方位角，一般以正北、正南为基准，用向东或向西旋转的角度表示方向.② 书写 通常要先写北或南，再写偏东或偏西.重点解析1如图，BD 平分∠ABC，BE 把∠ABC 分成 2:5 两部分，∠DBE=21°，求∠ABC 的度数. 解：设∠ABE = 2x°，则∠CBE = 5x°, ∠ABC =∠ABE+∠CBE= 7x°. 因为 BD 平分∠ABC，因为∠ABE+∠DBE =∠ABD ，即 2x + 21= 3.5x. 解得 x = 14.所以∠ABC = 7x°= 7×14°= 98°.重点解析2如图，∠AOB 是直角， ON是∠AOC 的平分线，OM 是∠BOC 的平分线.(1) 当∠AOC=50°时，求∠MON 的大小；所以∠MON=∠COM－∠CON=70°－25°=45°.解：因为∠AOB 是直角，∠AOC=50°， 所以∠BOC =∠AOB+∠AOC = 90°+50°=140°，因为ON 是∠AOC 的平分线，OM 是∠BOC 的平分线，  重点解析2(2) 当∠AOC＝α 时， ∠MON 等于多少度？ 解：∠BOC=∠AOB+∠AOC = 90°+α，因为ON是∠AOC 的平分线， OM是∠BOC 的平分线，  如图，∠AOB 是直角， ON是∠AOC 的平分线，OM 是∠BOC 的平分线.重点解析2(3) 当锐角∠AOC 的大小发生改变时，∠MON 的大小也会发生改变吗？为什么？解：不会发生变化. 由(2)可知∠MON 的大小与∠AOC无关， 总是等于∠AOB的一半. 如图，∠AOB 是直角， ON是∠AOC 的平分线，OM 是∠BOC 的平分线.重点解析3已知∠α 和∠β 互为补角，并且∠β 的一半比∠α 小30º，求∠α，∠β． 解：设∠α＝xº，则∠β＝180º－xº．根据题意 ∠β＝2(∠α－30º)，得 180－ x＝2(x －30)，解得 x＝80．所以 ，∠α＝80º，∠β＝100º．重点解析4如图，直线AB，CD 相交于点O，OF 平分∠AOE，∠FOD=90°．(1) 写出图中所有与∠AOD 互补的角；解：因为直线AB，CD 相交于点O， 所以∠AOC，∠BOD 与∠AOD 互补， 因为OF 平分∠AOE，所以∠AOF=∠EOF， 因为∠FOD=90°，所以∠COF=180°－∠FOD=90°. 又因为∠AOC=∠COF－∠AOF=90°－∠AOF=90°－∠EOF， ∠DOE=∠FOD－∠EOF=90°－∠EOF， 所以∠AOC=∠DOE. 所以与∠AOD互补的角有∠AOC，∠BOD，∠DOE.重点解析4(2) 若∠AOE =120°，求∠BOD 的度数． 解：因为OF 平分∠AOE，由(1)知，∠COF =90°，所以∠AOC =∠COF－∠AOF=90°－60°=30°.由(1)知，∠AOC 和∠BOD 与∠AOD 互补，所以∠BOD =∠AOC =30°(同角的补角相等).如图，直线AB，CD 相交于点O，OF 平分∠AOE，∠FOD=90°．重点解析5已知∠AOB=90°，∠COD=90°，画出示意图并探究∠AOC 与∠BOD 的关系．解：如图①，因为∠AOB = 90°， ∠COD = 90°， 所以∠AOC = 90°－∠BOC， ∠BOD = 90°－∠BOC， 所以∠AOC =∠BOD；重点解析5解：如图②，∠AOC=90°+∠BOC， ∠BOD=90°－∠BOC， 所以∠AOC+∠BOD=180°；已知∠AOB=90°，∠COD=90°，画出示意图并探究∠AOC 与∠BOD 的关系．重点解析5解：如图③，因为∠AOB=90°,∠COD=90°， 所以∠AOC=90°+∠BOC， ∠BOD=90°+∠BOC， 所以∠AOC=∠BOD；已知∠AOB=90°，∠COD=90°，画出示意图并探究∠AOC 与∠BOD 的关系．重点解析5解：如图④，∠AOC+∠BOD=360°－90°×2=180°， 所以∠AOC+∠BOD=180°． 综上所述，∠AOC =∠BOD 或 ∠AOC+∠BOD=180°．已知∠AOB=90°，∠COD=90°，画出示意图并探究∠AOC 与∠BOD 的关系．深化练习1(1)若∠A = 20°18′，∠B = 20°15′30″，∠C = 20.25°， 则( )A. ∠A＞∠B＞∠C B. ∠B＞∠A＞∠CC. ∠A＞∠C＞∠B D. ∠C＞∠A＞∠BA (2) 19点整时，时钟上时针与分钟 之间的夹角是( ) A. 210° B. 30° C. 150° D. 60°C深化练习2解：有两种情况： 如图①所示： ∠AOC =∠AOB+∠BOC =50°+10° =60°；已知一条射线 OA，若从点 O 再引两条射线 OB 和 OC，使∠AOB=50°，∠BOC=10°，求∠AOC 的度数．深化练习2 如图②所示： ∠AOC =∠AOB－∠BOC =50°－10° =40°. 综上所述，∠AOC 的度数为60°或40°．已知一条射线 OA，若从点 O 再引两条射线 OB 和 OC，使∠AOB=50°，∠BOC=10°，求∠AOC 的度数．