广东省揭阳市揭东区2021-2022学年九年级上学期期末数学试题（word版 含答案）

2021-2022学年度第一学期期末教学质量监测

九年级数学科试题

温馨提示：请将答案写在答题卡上。考试时间：20分钟满分120分

一、选择题（本大题共10小题，每小题3分，共30分）

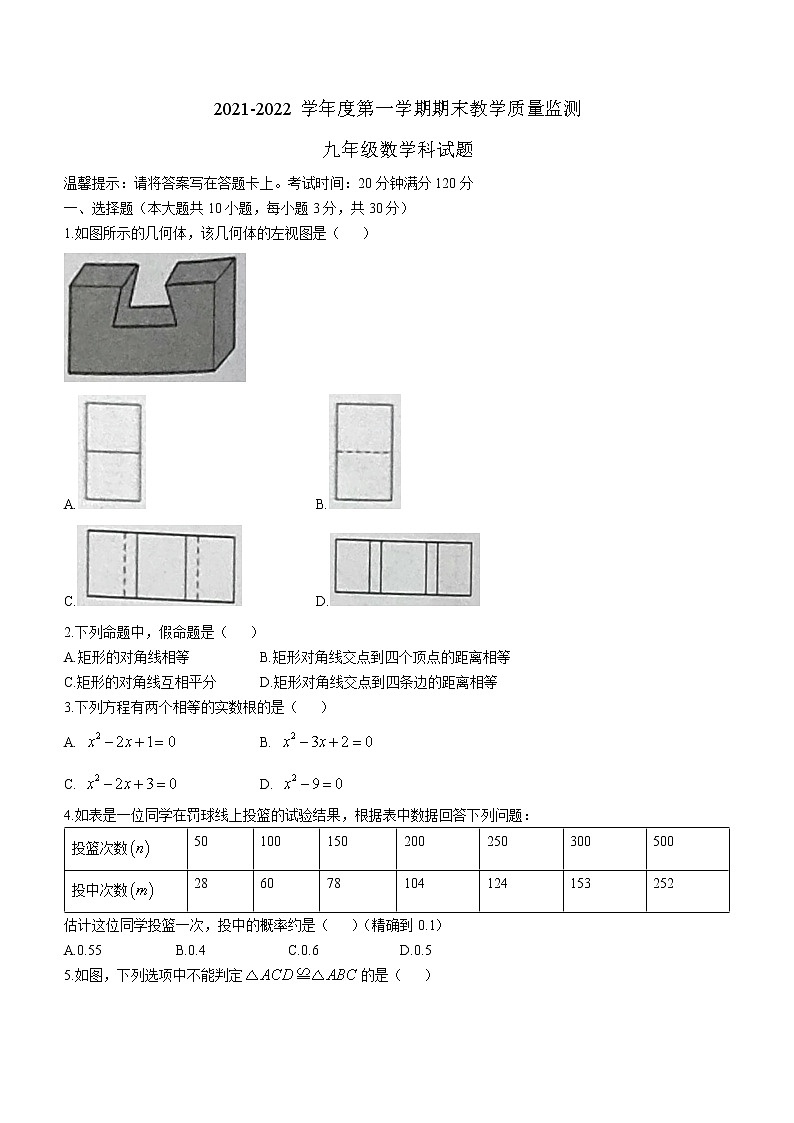
1.如图所示的几何体，该几何体的左视图是（   ）

A.       B.

C.   D.

2.下列命题中，假命题是（   ）

A.矩形的对角线相等   B.矩形对角线交点到四个顶点的距离相等

C.矩形的对角线互相平分  D.矩形对角线交点到四条边的距离相等

3.下列方程有两个相等的实数根的是（   ）

A.    B.

C.    D.

4.如表是一位同学在罚球线上投篮的试验结果，根据表中数据回答下列问题：

估计这位同学投篮一次，投中的概率约是（   ）（精确到0.1）

A.0.55   B.0.4   C.0.6   D.0.5

5.如图，下列选项中不能判定的是（   ）

A.    B.    C.    D.

6.下列四幅图中，能表示两棵树在同一时刻太阳光下的影子的图是（   ）

A.  B.

C.  D.

7.如图，在5×4的正方形网格中，每个小正方形的边长都是1，的顶点都在这些小正方形的顶点上，则的值为（   ）

A.    B.    C.    D.

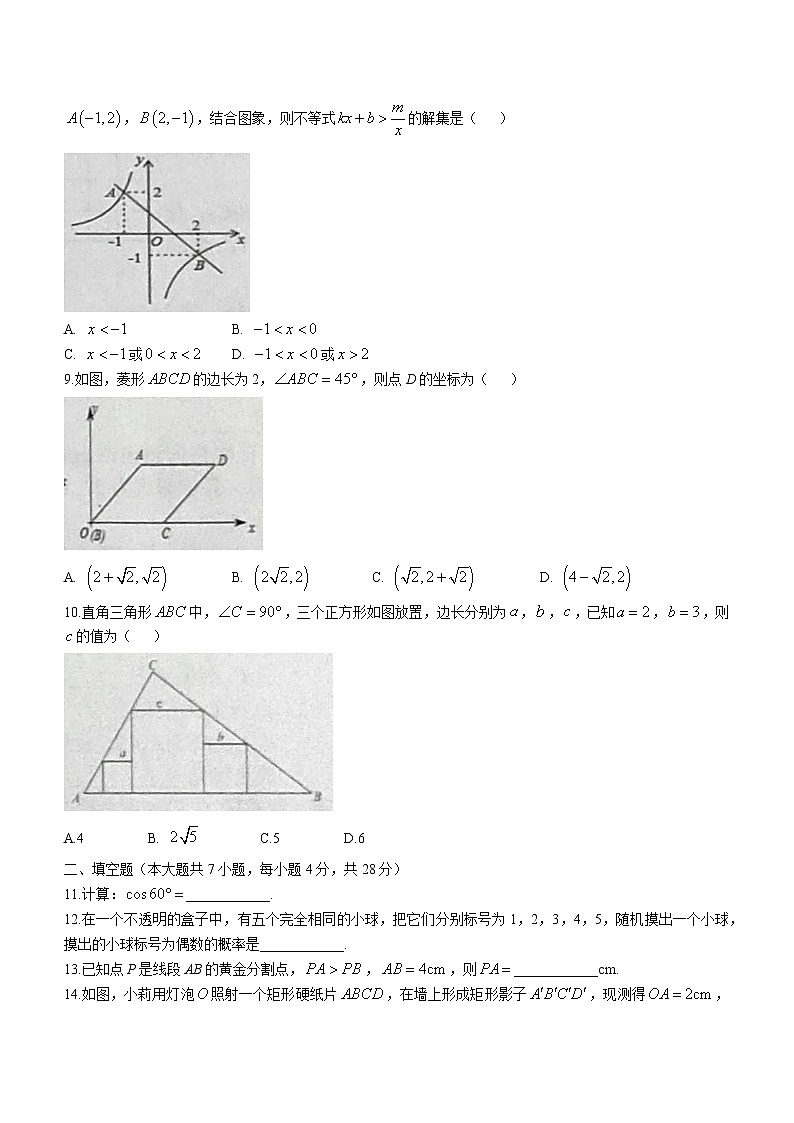
8.如图，一次函数的图象与反比例函数（为常数且）的图象都经过，，结合图象，则不等式的解集是（   ）

A.     B.

C. 或  D. 或

9.如图，菱形的边长为2，，则点D的坐标为（   ）

A.    B.    C.    D.

10.直角三角形中，，三个正方形如图放置，边长分别为，，，已知，，则的值为（   ）

A.4   B.    C.5   D.6

二、填空题（本大题共7小题，每小题4分，共28分）

11.计算：____________.

12.在一个不透明的盒子中，有五个完全相同的小球，把它们分别标号为1，2，3，4，5，随机摸出一个小球，摸出的小球标号为偶数的概率是____________.

13.已知点P是线段AB的黄金分割点，，，则____________cm.

14.如图，小莉用灯泡照射一个矩形硬纸片，在墙上形成矩形影子，现测得，，纸片ABCD的面积为，则影子的面积为_____________.

15.如图，矩形ABCD的两条对角线相交于点O，已知，，则矩形对角线BD的长为_____________cm.

16.如图6，在中，，，.则AB边的长为_____________.

17.如图，正方形OABC中，A，C分别在x，y轴正半轴上，反比例函数的图象与边BC，BA分别交于点D，E，且，对角线AC把分成面积相等的两部分，则_____________.

三、解答题（一）（本大题共3小题，每小题6分，共18分）

18.计算：.

19.解方程：.

20.已知：在平面直角坐标内，三个顶点的坐标分别为、、（正方形网格中每个小正方形的边长是一个单位长度）.

（1）画出向下平移5个单位长度得到的，点的坐标是___________.

（2）以点B为位似中心，在网格内画出，使与位似，且位似比为2：1，点的坐标是___________.

四、解答题（二）（本大题共3小题，每小题8分，共24分）

21.四川省某地区为了了解2021年初中毕业生毕业去向，对部分九年级学生进行了抽样调查，就九年级学生毕业后的四种去向：A.读普通高中，B.读职业高中，C.直接进入社会就业，D.其他（如出国等），进行数据统计，并绘制了两幅不完整的统计图.

（1）该地区共调查了____________名九年级学生；

（2）将两幅统计图中不完整的部分补充完整；

（3）老师想从甲、乙、丙、丁4位同学中随机选择两位同学了解他们毕业后的去向情况，请用画树状图或列表法求选中甲同学的概率.

22.如图，矩形ABCD中，M为BC上一点，交AD的延长线于点E.

①求证：.

②若，，求的值.

23.校内数学兴趣小组组织了一次测量探究活动.如图，大楼的顶部竖有一块广告牌CD，小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°，沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度，米，米，（量角器的高度忽略不计，结果精确到0.1米，参考数据：，，，，）

（1）求点B距离水平地面AE的高度；

（2）求广告牌CD的高度.

五、解答题（三）（本大题共2小题，每小题10分，共20分）

24.如图，过点分别作轴，轴，垂足分别为点B和点A，点F是线段BC上一个动点，但不与点B、点C重合，反比例函数的图象过点F，与线段AC交于点E，连接EF.

（1）当点E是线段AC的中点时，求点F的坐标；

（2）连接AB，试判断EF与AB的位置关系，并说明理由；

（3）若的面积为6，求反比例函数的表达式，

25.如图，在中，，，，点P从点B出发，以每秒2个单位的速度向A运动，同时，点Q从C出发，以每秒1个单位的速度向B运动，当一个点到达终点时，另一个点随之停止运动.连结PQ，在射线PB上截取，以PN、PQ为边作.设运动时间为t秒.

（1）的长为__________.

（2）当为正方形时，求的值，

（3）作点C关于直线PQ的对称点，当点C、Q、不共线，且等于内角的2倍时，求的值.

2021-2022学年度第一学期期末教学质量监测

九年级数学科参考答案

一、选择题

1-5BDADB    6-10ACCAC

二、填空题

11.     12.     13.     14.50    15.5    16. 17.

三、解答题（一）

18.解：原式.

19.解：整理，得：，∴，

则或，

解得，.

20.解：（1）

画图正确

（2）

画图正确

四、解答题二

解：（1）该地区调查的九年级学生数为：110÷55%=200（名），

故答案为：200；

（2）B去向的学生有：200-110-16-4=70（人），

C去向所占的百分比为：16÷200×100%=8%，

补全的统计图如右图所示，

（3）如图：

∵共有12种等可能的结果，其中选中甲同学的有6种，

∴，即选中甲同学的概率是.

22.（1）证明：∵四边形ABCD为矩形，

∴∠B=90°，AD∥BC，∴∠EAM=∠AMB，

∵EM⊥AM，∴∠AME=90°，

∵∠B=∠AME，∠AMB=∠EAM，

∴△ABM∽△EMA；

（2）解：∵△ABM∽△EMA，∴∠E=∠BAM，

在中，，

∴，∴；

23.解：（1）如图，过点B作BM⊥AE，BN⊥CE，垂足分别为M、N，

由题意可知，，，，米，米，

∵，

∴，∴（米），

即点B距水平地面AE的高度为6米；

（2）在中，

∴（米），（米），

∴米，

∵，

∴米，

∴米，

在中，，米，

∴（米），

∴（米）

答：广告牌CD的高约8.4米.

五、解答题（三）

24.解：（1）∵点E是线段AC的中点，∴，

∵点E在反比例函数的图象上，

∴，∴，

当时，，∴；

（2），理由如下：

∵轴，轴，，

∴四边形是矩形，

∵E、F都在反比例函数上，

∴，，

∴，，

在中，，

，

在中，，

，

∴，

∴.

（3）∵的面积为6，

∴，∴ .

解得，（舍去），

∴反比例函数的解析式为.

25.解：（1）在中，

∵，，，

∴，

∴的长为20，

故答案为：20.

（2）如图1，∵四边形PQMN是正方形，

∴，∴，∴，

∵，，

∴，∴.

（3）延长到点，

①如图2，，则，

∵与关于直线对称，

∴，

∴，∴，

∴，

由（2）得；

②如图3，，则，过点P作与点H

∵，

∴，∴，∴

∵即

解得：，

综上所述，或.